Квадратичные формы - определение и понятие с примерами решения

Содержание:

Первоначально теория квадратичных форм использовалась для исследования кривых и поверхностей, задаваемых уравнением второго порядка, содержащими две или три переменные, Позднее эта теория нашла и другие приложения. В частности, при математическом моделировании экономических процессов целевые функции могут содержать квадратичные слагаемые. Многочисленные приложения квадратичных форм потребовали построения общей теории, когда число переменных равно любому п, а коэффициенты квадратичной формы не всегда являются вещественными числами.

Понятие квадратичной формы

Квадратичной формой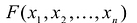

Пример:

Сумма 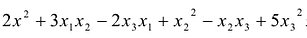является квадратичной формой от трех неизвестных .

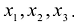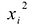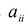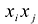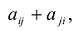Каждую квадратичную форму можно записать в стандартном виде. Для этого сначала приводятся подобные в квадратичной форме, затем коэффициенты при обозначаются через а коэффициенты при через причем 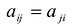„ Член 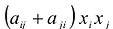записывается в виде 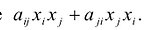После этих преобразований квадратичную форму можно записать в виде: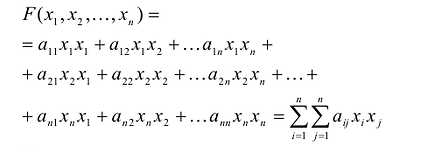

Матрица: 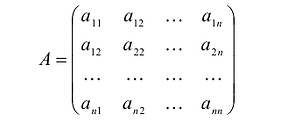называется матрицей квадратичной формы F. Так как 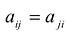то А - симметричная матрица.

С учетом правила умножения матриц можно вывести матричную форму записи квадратичной формы.

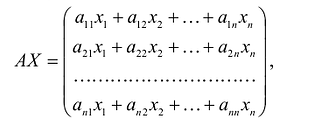
где А - матрица квадратичной формы, X - матрица-столбец неизвестных:

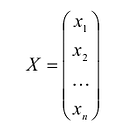
Приведенные выкладки показывают, в частности, что если А -симметрическая матрица, то выражение 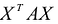является квадратичной формой от неизвестных 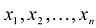,т.е. квадратичная форма является

результатом скалярного произведения матриц X и АХ. Матричная форма записи квадратичной формы имеет вид 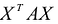. Если 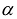- произвольный n— мерный вектор, то после подстановки в квадратичную форму 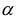вместо X получится число 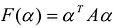, которое называется значением квадратичной формы F(X) на векторе .

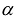Канонический базис квадратичной формы

Принято считать, что квадратичная форма F(X) имеет канонический вид, если все коэффициенты при произведениях различных переменных равны нулю, т.е. 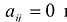при 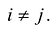. При этом квадратичная форма представляет собой сумму квадратов переменных с соответствующими коэффициентами 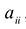,т.е.:

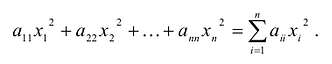
В этом случае матрица квадратичной формы имеет диагональный вид:

Очевидно, что изучение свойств квадратичной формы, записанной в каноническом виде, значительно упрощается. В связи с этим возникает задача приведения произвольной квадратичной формы к каноническому виду. В основе многих известных методов приведения квадратичной формы к каноническому виду лежит следующая теорема.

Теорема. Всякая квадратичная форма с помощью невырожденного линейного преобразования может быть приведена к каноническому виду.

Метод ортогональной матрицы использует особенности собственных значений и собственных векторов симметрической матрицы.

Пусть дана квадратичная форма 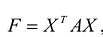, Поскольку А -симметрическая матрица, для нее существует диагонализирующая ортогональная матрица S, такая что:

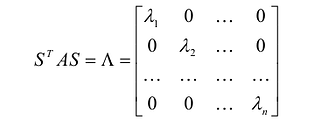
где 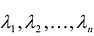-собственные значения матрицы А.

Применим к квадратичной форме линейное преобразование 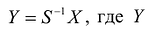- матрица-столбец новых переменных 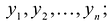- матрица, обратная к S.

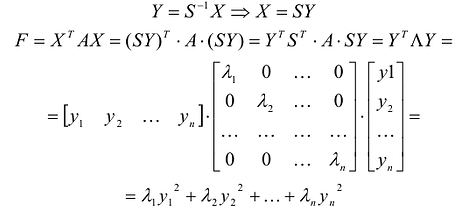
Таким образом, квадратичную форму всегда можно представить в каноническом виде с коэффициентами, равными собственным значениям матрицы квадратичной формы.

Канонический вид квадратичной формы определяется неоднозначно. В то же время можно доказать, что все канонические формы, к которым приводится данная квадратичная форма, содержат одинаковое число отрицательных, положительных и нулевых коэффициентов при квадратах новых переменных.

Наиболее удобным для исследования является канонический вид, в котором коэффициенты при новых переменных равны +1 или -1, т.е. квадратичная форма имеет вид:

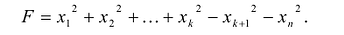
Такую запись называют нормальным видом квадратичной формы. В нем общее число квадратов равно рангу r квадратичной формы.

Квадратичная форма может быть приведена к нормальному виду многими различными преобразованиями. При этом справедлива следующая теорема.

Теорема, Число положительных и число отрицательных квадратов в нормальном виде, к которому приводится данная вещественная квадратичная форма вещественным невырожденным линейным преобразованием, не зависит от выбора этого преобразования.

Эту теорему называют законом инерции квадратичных форм.

Базис пространства R" называется каноническим базисом квадратичной формы 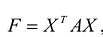, если в этом базисе квадратичная форма имеет канонический вид, т.е. 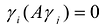при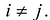

Если канонический базис F(X), то выражение: 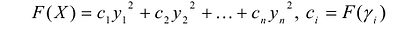называется каноническим видом F(X) в базисе где - новый набор неизвестных.

Теорема. Если 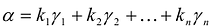- разложение вектора а по каноническому базису квадратичной формы 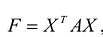то значение F(X) на векторе а вычисляется по формуле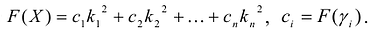

Доказательство:

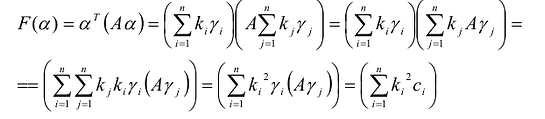
Эта теорема утверждает, что если известны канонический базис квадратичной формы F(X) и ее канонический вид 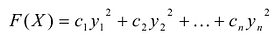в этом базисе, то для вычисления значения F(a) квадратичной формы F(X) на векторе а достаточно:

1. разложить вектор а по каноническому базису :
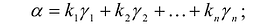
2. коэффициенты разложения 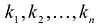подставить вместо неизвестных в канонический вид квадратичной формы: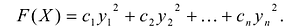

Квадратичная форма имеет много разных канонических базисов. Процесс построения канонического базиса называется приведением квадратичной формы к сумме квадратов.

Наиболее часто используются: канонический базис из собственных векторов матрицы А и канонический базис Якоби.

Канонический базис из собственных векторов матрицы квадратичной формы

Теорема. Ортонормированный базис пространства Rсостоящий из собственных векторов симметрической матрицы 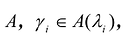, является каноническим базисом квадратичной формы 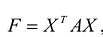, а выражение 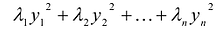- ее каноническим видом в базисе ,

Доказательство:

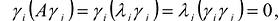• , если 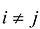так как -ортогональная система векторов => ,- канонический базис квадратичной формы F(X).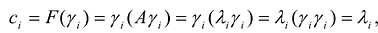
• = так как векторы системы нормированы, то .

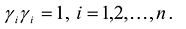Канонический базис Якоби квадратичной формы 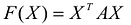. Будем говорить, что матрица 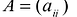удовлетворяет условию Якоби, если определители:

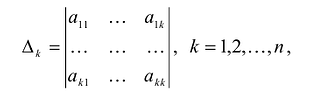
называемые угловыми минорами матрицы А, не равны нулю. Очевидно, что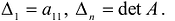

Обозначим через 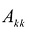матрицу:

Вычислим определитель этой матрицы, разлагая ее по последнему столбцу, затем также по последнему столбцу разложим полученный определитель и т.д. 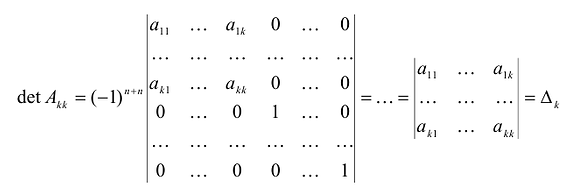Из условия 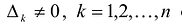следует, что 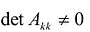и, значит, каждая система уравнений 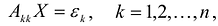, где 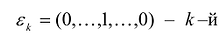вектор диагональной системы, имеет единственное решение 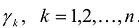. Система векторов называется системой векторов Якоби матрицы А, которая удовлетворяет условию Якоби.

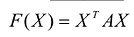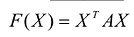Теорема. матрица А квадратичной формы удовлетворяет условию Якоби, система векторов Якоби матрицы А является каноническим базисом квадратичной формы , а выражение:

ее каноническим видом в базисе .

Положительно и отрицательно определенные квадратичные формы

Квадратичная форма F{X) называется положительно определенной, если значение F(X) на каждом ненулевом значении а больше нуля, т.е.:

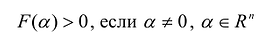
Если же F(a) < 0 на каждом 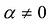, то квадратичная форма называется отрицательно определенной.

Теорема. Дана квадратичная форма 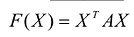, ее канонический базис, л выражение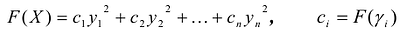

канонический вид 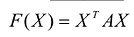в базисе . Тогда справедливы следующие утверждения:

1. Квадратичная форма F(X) положительно определена тогда и только тогда, когда .
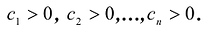2. Квадратичная форма F{X) отрицательно определена тогда и только тогда, когда

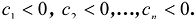
Доказательство:

Необходимость. Дано, что F(X) - положительно определенная форма. Так как 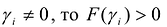и поэтому .

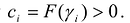Достаточность. Дано, что в каноническом виде все коэффициенты 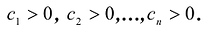Нужно доказать, что F(X) положительно определена. Рассмотрим произвольный ненулевой вектор а и разложим его по базису :

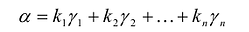
Так как 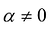, то в разложении 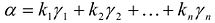не все коэффициенты равны нулю. Следовательно 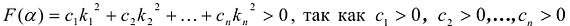и среди чисел 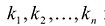хотя бы одно отлично от нуля.

Аналогично доказывается и второе утверждение.

Эта теорема дает два наиболее употребляемых критерия положительной и отрицательной определенности квадратичной формы.

Теорема. Дана квадратичная форма 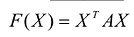. Тогда справедливы следующие утверждения:

1. Квадратичная форма F(X) положительно определена тогда и только тогда, когда все собственные значения матрицы А положительны.
2. Квадратичная форма F(X) отрицательно определена тогда и только тогда, когда все собственные значения матрицы А отрицательны.

• Заказать решение задач по высшей математике

Доказательство:

Докажем первое утверждение. Рассмотрим ортонормированный базис пространства R", состоящий из собственных векторов симметрической матрицы А, и пусть 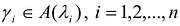. Тогда канонический базис квадратичной формы F(X), а выражение 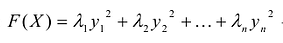- ее канонический вид в базисе . Теперь первое утверждение этой теоремы вытекает из первого предложения предыдущей теоремы.

Второе предложение доказывается аналогично.

Лемма. Если какой-нибудь угловой минор 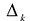матрицы А равен нулю у то найдется такой ненулевой вектор 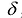, что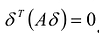

Теорема (Критерий Сильвестра). Справедливы следующие утверждения:

1. Квадратичная форма 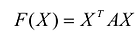положительно определена тогда и только тогда, когда главные миноры матрицы А положительны.
2. Квадратичная форма 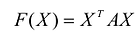отрицательно определена тогда и только тогда, когда главные миноры матрицы А четного порядка положительны, а главные миноры матрицы А нечетного порядка отрицательны.

Доказательство: Докажем первое утверждение.

Необходимость. Дано, что F(X) положительно определена. Покажем, что все угловые миноры матрицы А отличны от нуля. Допустим обратное, и пусть 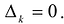. Тогда согласно Лемме найдется такой ненулевой вектор 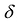, что 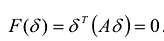. Однако это противоречит положительной определенности квадратичной формы.

Итак, матрица А удовлетворяет условию Якоби, поэтому можно построить систему векторов Якоби , которая является каноническим базисом F(X), причем выражение 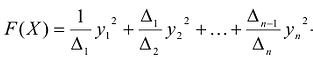- ее канонический вид в базисе . Теперь из положительной определенности квадратичной формы и первого утверждения доказанной ранее теоремы следует,

что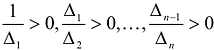, и значит, что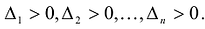

Достаточность. Если 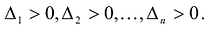, то угловые миноры матрицы А отличны от нуля, и можно построить канонический базис квадратичной формы F(X), в котором 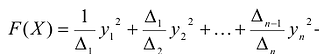- канонический вид квадратичной формы F(X). Поскольку 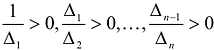, то F(X) положительно определена.

Аналогично доказывается второе утверждение теоремы.

Применение квадратичных форм к исследованию кривых второго прядка

В общем случае кривая второго порядка в базисе 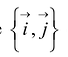описывается уравнением 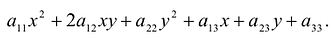. Ее первые три слагаемые образуют квадратичную форму 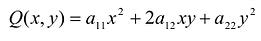с матрицей:

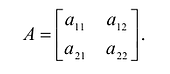
Задача о приведении кривой 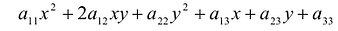, к каноническому виду сводится к задаче о приведении к каноническому виду квадратичной формы Q (х,у) этой кривой.

Пусть 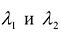- собственные значения матрицы 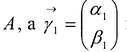и 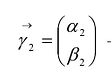ортонормированные собственные векторы матрицы А, соответствующие собственным значениям .

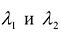Ортонормированные векторы 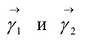называются главными направлениями этой кривой.

Пусть 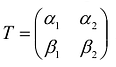является матрицей перехода от ортонормированного базиса к ортонормированному базису 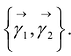Тогда ортогональное преобразование: 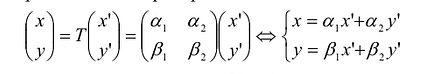приводит квадратичную форму Q (х,у) к каноническому виду 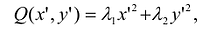, а уравнение кривой - к виду 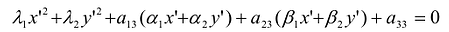в прямоугольной декартовой системе координат 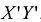, оси которой направлены вдоль 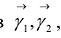векторов, а начало совпадает с точкой О системы координат XY.

Выделив в этом уравнении полные квадраты, получим 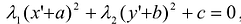, где а,Ь,с - некоторые числа. Осуществив параллельный перенос системы координат 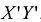в новое начало 0 = (-а—Ь), получим канонический вид уравнения

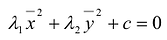в системе координат 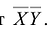. В зависимости от чисел 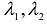,с эта кривая будет эллипсом, гиперболой, параболой, парой прямых, точкой или мнимой кривой.