
Многогранники - виды, свойства и определения с примерами решения
Содержание:
Граничные точки фигуры:
В курсе планиметрии и в начале изучения стереометрии было дано описание некоторых пространственных геометрических фигур, которые называются многогранниками. Теперь уточним понятие многогранника, познакомимся с новыми свойствами многогранников и систематизируем известные сведения о них.
Как уже отмечалось, в стереометрии изучаются не только плоские, но и пространственные геометрические фигуры, т. е. фигуры, не все точки которых лежат в одной плоскости. Примерами пространственных фигур служат геометрические тела, в частности многогранники.
Наглядно геометрическое тело можно представить себе как часть пространства, занятую физическим телом (рис. 1, а, б, в). Для того чтобы дать определение геометрического тела, прежде определим некоторые вспомогательные понятия.
Точка М называется граничной точкой фигуры F, расположенной в пространстве, если на сколь угодно малом расстоянии от точки М найдутся точки как принадлежащие фигуре F, так и не принадлежащие этой фигуре.
Иначе говоря, точка называется граничной точкой фигуры в пространстве, если в любом шаре с центром в этой точке есть точки, принадлежащие этой фигуре, и точки, не принадлежащие ей.
Заметим, что граничные точки фигуры F могут не принадлежать этой фигуре.
Например, пусть F — фигура, состоящая из точек куба, за исключением точек некоторой его грани Тогда каждая точка грани F, является граничной точкой фигуры F, но не принадлежит F.
Множество всех граничных точек фигуры называется ее границей.
Заметим, что граница фигуры не всегда совпадает с самой фигурой.
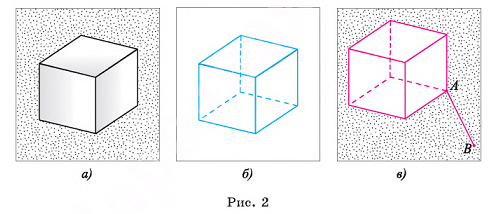
Например, границей куба является фигура, образованная его гранями, т. е. поверхность куба (рис. 2, а, б). Границей шара с центром в точке О и радиусом R служит сфера с центром в точке О, имеющая тот же радиус R.
Границей фигуры, представляющей собой объединение куба и отрезка АВ, служит фигура, которая является объединением поверхности этого куба и отрезка АВ (рис. 2, в).
Внутренние точки фигуры:
Определим понятие внутренней точки фигуры, расположенной в пространстве.
Точка М называется внутренней точкой фигуры F, расположенной в пространстве, если найдется такое положительное число е, что любая точка, находящаяся от точки М на расстоянии, меньшем е, принадлежит фигуре F.
Иначе говоря, точка называется внутренней точкой фигуры, если существует шар с центром в этой точке, каждая точка которого принадлежит фигуре.
Заметим, что внутренняя точка фигуры F всегда принадлежит этой фигуре.
Любая точка куба, не принадлежащая его граням, является внутренней точкой куба.
Фигура может не иметь внутренних точек, например плоскость в пространстве. Действительно, для любой точки плоскости не существует шара с центром в этой точке, все точки которого лежат в этой плоскости.
Множество всех внутренних точек фигуры называется ее внутренностью.
Например, внутренность куба есть фигура, образованная точками куба, которые не принадлежат его граням.
Фигура пространства называется ограниченной, если существует такое положительное число d, что расстояние между любыми двумя точками этой фигуры меньше этого числа d.
Другими словами, фигура называется ограниченной, если все ее точки принадлежат некоторому шару.
Геометрические тела и многогранники
Теперь можем охарактеризовать геометрическое тело.
Геометрическим телом называется ограниченная фигура в пространстве, обладающая следующими свойствами:
- у нее есть внутренние точки, и любые две из них можно соединить ломаной, каждая точка которой является внутренней точкой фигуры;
- фигура содержит свою границу, и ее граница совпадает с границей ее внутренности.
Например, множество точек пространства, находящихся от точки О на расстоянии, меньшем или равном данному числу R, т. е. шар с центром в точке О и радиусом R, является телом. В то же время множество точек, находящихся от точки О на расстоянии, меньшем R, не является телом, так как не выполняется второе свойство.
Плоскость в пространстве не является телом, так как ни одна из ее точек не является внутренней.
Граница тела называется его поверхностью.
Многогранником называется геометрическое тело, поверхность которого состоит из конечного числа многоугольников, любые два из которых, имеющие общую сторону, не лежат в одной плоскости.
Многоугольники, образующие границу многогранника, называются гранями, их стороны — ребрами, а вершины — вершинами многогранника.
Представление о многогранниках дают кристаллы природных минералов (рис. 3, а).
Плоским, углом при вершине О многогранника называется угол грани многогранника с вершиной в точке О.
Например, на рисунке 3, б изображен многогранник — октаэдр, у которого восемь граней. Углы ОАВ, OAD, BAF и DAF — плоские углы при вершине А октаэдра.
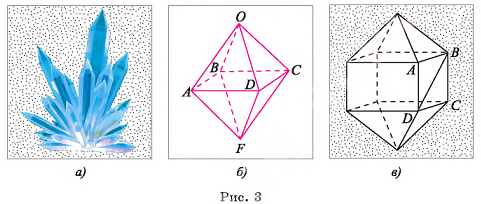
Многогранник, изображенный на рисунке 3, в, имеет двенадцать граней и десять вершин.
Заметим, что треугольники ABD и BCD, имеющие общую сторону BD, не являются гранями многогранника, изображенного на рисунке 3, в, так как не лежат в разных плоскостях. Отрезок DB не является ребром этого многогранника, так как не является стороной грани.
Фигура, являющаяся объединением двух кубов, имеющих одну общую вершину О (рис. 4, а), не является многогранником, поскольку она не является геометрическим телом, так как, например, внутренние точки А и В этой фигуры нельзя соединить ломаной, каждая точка которой является внутренней точкой фигуры. Действительно, любая ломаная, состоящая из точек фигуры и соединяющая точки А и В, содержит точку О, которая не является внутренней точкой указанной фигуры.
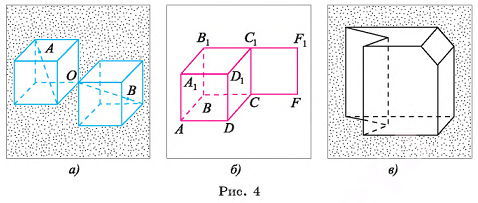
Фигура, состоящая из куба 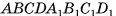 и квадрата
и квадрата 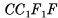 (рис. 4, б), не является геометрическим телом, а следовательно, не является многогранником. Действительно, границей внутренности этой фигуры служит поверхность куба
(рис. 4, б), не является геометрическим телом, а следовательно, не является многогранником. Действительно, границей внутренности этой фигуры служит поверхность куба 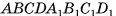 , а граница всей фигуры состоит из поверхности куба и точек квадрата
, а граница всей фигуры состоит из поверхности куба и точек квадрата 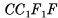 , т. е. граница указанной фигуры не совпадает с границей ее внутренности.
, т. е. граница указанной фигуры не совпадает с границей ее внутренности.
Среди множества многогранников выделяются выпуклые и невыпуклые многогранники.
Многогранник называется выпуклым, если он расположен по одну сторону от каждой из плоскостей, содержащих его грани.
Многогранник называется невыпуклым, если существует такая его грань, что он лежит по разные стороны от плоскости, содержащей эту грань.
Например, октаэдр (см. рис. 3, б) — выпуклый многогранник, а многогранник, изображенный на рисунке 4, в, — невыпуклый.
В дальнейшем, если не оговорено иное, будем рассматривать выпуклые многогранники.
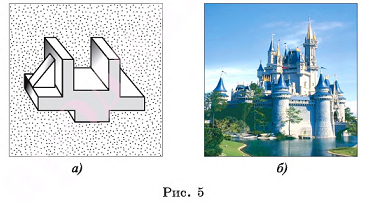
Многие детали, применяемые в машиностроении и других производствах, архитектурные сооружения имеют форму многогранников. Например, на рисунке 5, а изображена деталь, имеющая форму невыпуклого многогранника. Различные архитектурные сооружения имеют форму некоторых геометрических тел (рис. 5, б).
Призма
В данном параграфе систематизируем сведения о призме и параллелепипеде.
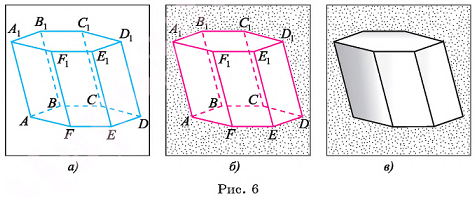
Определение. Призмой (n-угольной) называется многогранник, у которого две грани — равные n-угольники  (называемые основаниями) с соответственно параллельными сторонами
(называемые основаниями) с соответственно параллельными сторонами 
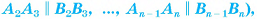 а остальные n граней — параллелограммы, у каждого из которых две стороны являются соответственными сторонами оснований.
а остальные n граней — параллелограммы, у каждого из которых две стороны являются соответственными сторонами оснований.
Эти параллелограммы называются боковыми гранями призмы, а их стороны, не являющиеся сторонами основания призмы, называются боковыми ребрами призмы.
В дальнейшем будем рассматривать только выпуклые призмы.
Призма с основаниями 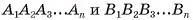 обозначается
обозначается 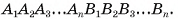 Например, на рисунке 6, а, б, в изображена шестиугольная призма с основаниями ABCDEF и
Например, на рисунке 6, а, б, в изображена шестиугольная призма с основаниями ABCDEF и 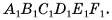
Фигура, образованная всеми гранями призмы, называется полной поверхностью призмы, а фигура, образованная боковыми гранями, — боковой поверхностью призмы.
Теорема 1 (о свойстве оснований призмы).
Основания призмы лежат в параллельных плоскостях.
Доказательство:
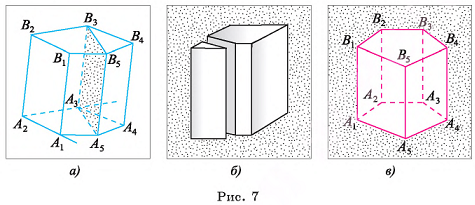
Пусть дана призма, основаниями которой являются « угольники 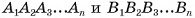 (на рисунке 7, а изображена пятиугольная призма). По определению призмы
(на рисунке 7, а изображена пятиугольная призма). По определению призмы 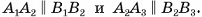 Таким образом, пересекающиеся прямые
Таким образом, пересекающиеся прямые 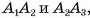 , лежащие в плоскости одного основания, соответственно параллельны прямым
, лежащие в плоскости одного основания, соответственно параллельны прямым 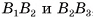 , лежащим в плоскости другого основания. Следовательно, по признаку параллельности плоскостей плоскости, содержащие основания
, лежащим в плоскости другого основания. Следовательно, по признаку параллельности плоскостей плоскости, содержащие основания 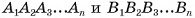 , параллельны.
, параллельны.
Теорема доказана.
Высотой призмы называется перпендикуляр (или длина этого перпендикуляра), проведенный из какой-нибудь точки плоскости одного основания к плоскости другого основания.
Прямая призма. Правильная призма
Среди множества призм выделяют такие, которые называются прямыми призмами.
Призма называется прямой, если все ее боковые грани являются прямоугольниками.
Представление о прямой призме дают, например, модели, которые получаются в результате распиливания деревянного бруска, имеющего форму прямоугольного параллелепипеда, вдоль ребра, как изображено на рисунке 7, б.
Призма, у которой не все боковые грани являются прямоугольниками, называется наклонной.
Теорема 2 (о свойстве боковых ребер прямой призмы).
Боковые ребра прямой призмы, перпендикулярны плоскостям, в которых лежат ее основания.
Доказательство.
Пусть дана прямая призма 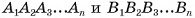 (на рисунке 7, в изображена прямая пятиугольная призма).
(на рисунке 7, в изображена прямая пятиугольная призма).
Докажем, например, что боковое ребро 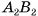 перпендикулярно плоскости, в которой лежит основание
перпендикулярно плоскости, в которой лежит основание 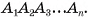 Так как по определению прямой призмы все ее боковые грани — прямоугольники, то четырехугольник
Так как по определению прямой призмы все ее боковые грани — прямоугольники, то четырехугольник 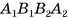 — прямоугольник, а, значит,
— прямоугольник, а, значит, 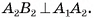 Аналогично четырехугольник
Аналогично четырехугольник 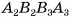 является прямоугольником, следовательно,
является прямоугольником, следовательно, 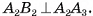 Таким образом, прямая
Таким образом, прямая 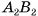 перпендикулярна двум пересекающимся прямым плоскости, содержащей основание
перпендикулярна двум пересекающимся прямым плоскости, содержащей основание 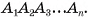 Следовательно, по признаку перпендикулярности прямой и плоскости прямая
Следовательно, по признаку перпендикулярности прямой и плоскости прямая 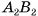 перпендикулярна этой плоскости. Основания
перпендикулярна этой плоскости. Основания 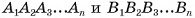 лежат в параллельных плоскостях, следовательно, ребро
лежат в параллельных плоскостях, следовательно, ребро 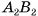 перпендикулярно также плоскости, в которой лежит основание
перпендикулярно также плоскости, в которой лежит основание 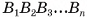 . Для остальных ребер доказательство аналогично.
. Для остальных ребер доказательство аналогично.
Теорема доказана.
Из теоремы следует, что высота прямой призмы равна ее боковому ребру.
У наклонной призмы боковые ребра не перпендикулярны к плоскостям, в которых лежат основания.
Определение. Призма называется правильной, если она прямая, а ее основаниями служат правильные многоугольники.
Диагональю призмы называется отрезок, концами которого служат вершины призмы, не лежащие в одной грани.
Диагональным, сечением призмы называется ее сечение плоскостью, проходящей через два боковых ребра, которые не лежат в одной грани.
Диагональное сечение любой наклонной призмы в общем случае — параллелограмм, а сечение прямой призмы — прямоугольник. Например, диагональное сечение 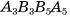 призмы
призмы 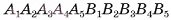 есть параллелограмм (см. рис. 7, а), так как
есть параллелограмм (см. рис. 7, а), так как 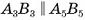 (боковые ребра призмы попарно параллельны), a
(боковые ребра призмы попарно параллельны), a 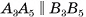 (основания призмы лежат в параллельных плоскостях, следовательно, секущая плоскость пересекает их по параллельным прямым).
(основания призмы лежат в параллельных плоскостях, следовательно, секущая плоскость пересекает их по параллельным прямым).
Если секущая плоскость пересекает все боковые ребра призмы и перпендикулярна им, то получающееся при этом сечение называется ортогональным, сечением призмы.
Площадью боковой поверхности призмы называется сумма площадей ее боковых граней (обозначается 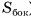 ).
).
Площадью полной поверхности призмы называется сумма площадей всех ее граней (обозначается 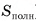 ).
).
Площадь полной поверхности призмы равна сумме площади ее боковой поверхности и удвоенной площади основания:
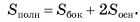
Теорема 3 (о площади боковой поверхности прямой призмы).
Площадь боковой поверхности прямой призмы, равна произведению периметра ее основания на высоту призмы 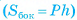 .
.
Доказательство.
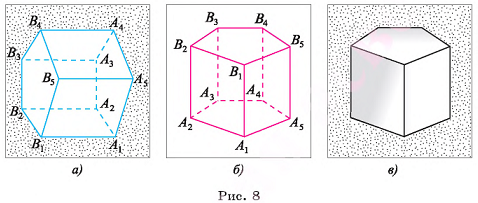
Пусть дана прямая призма 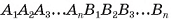 (на рисунке 8, а, б, в изображена пятиугольная призма), Р — периметр ее основания, h — высота этой призмы. Докажем, что площадь боковой поверхности
(на рисунке 8, а, б, в изображена пятиугольная призма), Р — периметр ее основания, h — высота этой призмы. Докажем, что площадь боковой поверхности 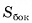 прямой призмы находится по формуле
прямой призмы находится по формуле 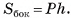
Боковые грани прямой призмы являются прямоугольниками, одна из сторон которых равна стороне основания призмы, а другая — высоте h призмы. Площадь боковой поверхности прямой призмы равна сумме площадей указанных прямоугольников, таким образом, 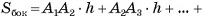
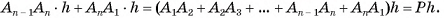
Теорема доказана.
Параллелепипед
Теперь рассмотрим понятие параллелепипеда.
Параллелепипед — это призма, основаниями которой являются параллелограммы.
Все шесть граней параллелепипеда — параллелограммы.
Две грани параллелепипеда, не имеющие общего ребра, называются противолежащими, а имеющие общее ребро — смежными.
Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими. Отрезок, соединяющий противолежащие вершины, называется диагональю параллелепипеда.
Параллелепипед называется прямым, если все его боковые грани — прямоугольники.
Параллелепипед называется наклонным, если не все его боковые грани являются прямоугольниками.
Параллелепипед называется прямоугольным., если все его грани — прямоугольники.
Длины трех ребер, выходящих из одной вершины, называются измерениями прямоугольного параллелепипеда.
Напомним свойства параллелепипеда.
- Противолежащие грани параллелепипеда равны и лежат в параллельных плоскостях.
- Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Свойство прямого параллелепипеда: боковые ребра прямого параллелепипеда перпендикулярны, плоскостям его оснований.
Свойство прямоугольного параллелепипеда: квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Пример №1
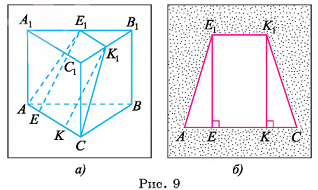
В правильной треугольной призме длина каждого ребра равна а. Найдите площадь сечения призмы плоскостью а, проходящей через сторону одного из оснований и среднюю линию другого основания.
Дано:
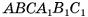 — правильная призма,
— правильная призма,
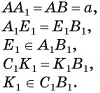
Найти: 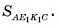
Многогранники
Решение:
1)Пусть точки 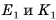 — середины ребер
— середины ребер 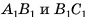 соответственно. Тогда секущая плоскость пересекает грани
соответственно. Тогда секущая плоскость пересекает грани 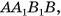
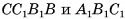 по отрезкам
по отрезкам 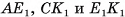 соответственно. Четырехугольник
соответственно. Четырехугольник 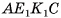 — сечение призмы плоскостью а.
— сечение призмы плоскостью а.
2)Четырехугольник 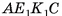 — равнобедренная трапеция (
— равнобедренная трапеция (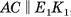 , так как
, так как 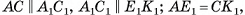 поскольку прямоугольные треугольники
поскольку прямоугольные треугольники 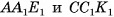 равны по двум катетам) (рис. 9, а, б).
равны по двум катетам) (рис. 9, а, б).
3)Для нахождения площади трапеции 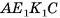 достаточно найти ее высоту (длины оснований трапеции:
достаточно найти ее высоту (длины оснований трапеции: 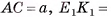
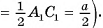
4) Пусть 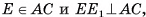 тогда
тогда 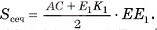
5) В треугольнике  длина гипотенузы
длина гипотенузы 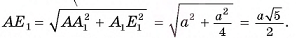
б) Пусть 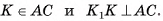 Из треугольника
Из треугольника 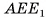
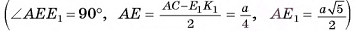 найдем
найдем 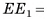
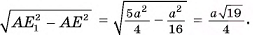 Следовательно,
Следовательно, 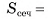
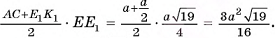
Ответ: 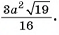
Пример №2
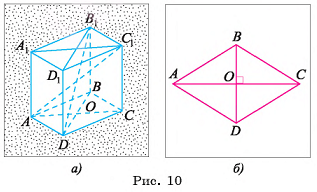
Основание прямого параллелепипеда — ромб, длина стороны которого а. Диагонали параллелепипеда образуют с основанием углы 30° и 45°. Найдите площади диагональных сечений параллелепипеда.
Дано:
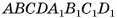 прямой параллелепипед, ABCD — ромб,
прямой параллелепипед, ABCD — ромб,
АВ = а,
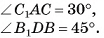
Найти: 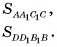
Решение:
1)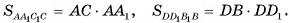 Следовательно, для нахождения площадей диагональных сечений необходимо найти длины диагоналей основания и высоту параллелепипеда (рис. 10, а).
Следовательно, для нахождения площадей диагональных сечений необходимо найти длины диагоналей основания и высоту параллелепипеда (рис. 10, а).
2)Пусть 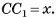 В треугольнике
В треугольнике 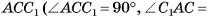
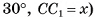 длина катета
длина катета 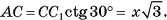
3)В треугольнике 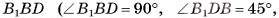
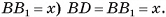
4)В треугольнике 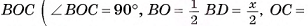
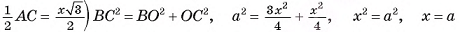
(рис. 10, а, б).
5)Таким образом, 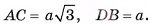 Теперь найдем
Теперь найдем 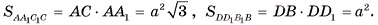
Ответ: 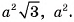
Пример №3
Докажите, что площадь боковой поверхности наклонной призмы равна произведению периметра ортогонального сечения на д.тину ее бокового ребра.
Доказательство.
Каждая грань призмы является параллелограммом. Площадь каждого параллелограмма равна произведению длины любой его стороны на высоту, проведенную к этой стороне. Следовательно, площадь ее боковой поверхности будет равна произведению длины бокового ребра на периметр ортогонального сечения призмы.
Пирамида
В предыдущих классах в процессе решения задач мы познакомились с некоторыми свойствами пирамид. Теперь систематизируем известные вам знания о пирамидах и рассмотрим некоторые другие их свойства.
Определение. Пирамидой (n-угольной) называется многогранник, у которого одна грань — некоторый n-угольник  , а остальные грани — треугольники
, а остальные грани — треугольники  с общей вершиной О. Указанный n-угольник
с общей вершиной О. Указанный n-угольник  называется основанием пирамиды, а треугольники
называется основанием пирамиды, а треугольники 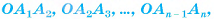
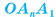 — боковыми гранями (рис. 15, а, б).
— боковыми гранями (рис. 15, а, б).
В дальнейшем будем рассматривать только выпуклые пирамиды.
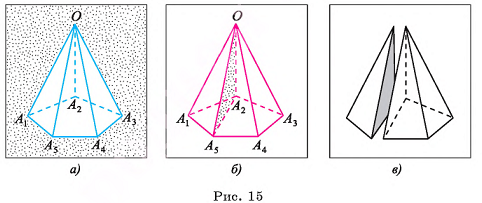
Точка О называется вершиной пирамиды, точки 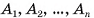 называются вершинами основания пирамиды.
называются вершинами основания пирамиды.
Отрезки 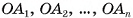 называются боковыми ребрами пирамиды.
называются боковыми ребрами пирамиды.
Пирамида с основанием 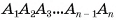 и вершиной О обозначается
и вершиной О обозначается 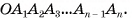
Фигура, образованная всеми гранями пирамиды, называется полной поверхностью пирамиды, а фигура, образованная боковыми гранями, — боковой поверхностью пирамиды.
Диагональным сечением пирамиды называется сечение ее плоскостью, проходящей через два боковых ребра пирамиды, не лежащих в одной грани. Например, 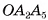 — диагональное сечение пирамиды
— диагональное сечение пирамиды 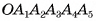 (см. рис. 15, б).
(см. рис. 15, б).
Любое диагональное сечение разбивает выпуклую пирамиду на две пирамиды. Например, диагональное сечение 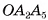 , разбивает пирамиду
, разбивает пирамиду 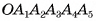 , на треугольную и четырехугольную пирамиды
, на треугольную и четырехугольную пирамиды 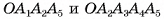 (рис. 15, б, в).
(рис. 15, б, в).
Высотой пирамиды называется перпендикуляр (или длина этого перпендикуляра), проведенный из вершины пирамиды к плоскости основания.
Площадью боковой поверхности пирамиды называется сумма площадей ее боковых граней (обозначается 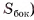 ).
).
Площадью полной поверхности пирамиды называется сумма площадей всех ее граней (обозначается 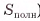 ).
).
Площадь полной поверхности пирамиды равна сумме площадей ее боковой поверхности и площади основания:
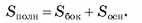
Правильная пирамида
Пирамида называется правильной, если ее основание — правильный n-угольник, а все боковые ребра равны.
Высота боковой грани правильной пирамиды, проведенная к стороне основания, называется апофемой правильной пирамиды.
Теорема 1 (о высоте правильной пирамиды). В правильной пирамиде отрезок, соединяющий вершину пирамиды, с центром ее основания, является высотой пирамиды.
Доказательство.
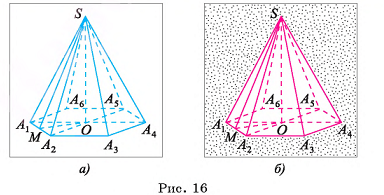
1) Пусть S — вершина правильной пирамиды 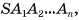 , а точка О — центр ее основания (на рисунке 16, а, б изображена правильная шестиугольная пирамида). Треугольник
, а точка О — центр ее основания (на рисунке 16, а, б изображена правильная шестиугольная пирамида). Треугольник 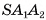 является равнобедренным, так как пирамида правильная, а, значит,
является равнобедренным, так как пирамида правильная, а, значит, 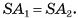 Треугольник
Треугольник 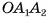 является равнобедренным, так как точка О — центр правильного многоугольника
является равнобедренным, так как точка О — центр правильного многоугольника 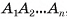 , а, значит,
, а, значит, 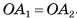 .
.
2)Пусть точка М — середина отрезка 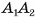 . Тогда
. Тогда 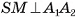 , так как медиана SM равнобедренного треугольника
, так как медиана SM равнобедренного треугольника 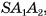 , проведенная к его основанию
, проведенная к его основанию 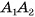 , является высотой. Аналогично
, является высотой. Аналогично 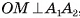 , так как ОМ — медиана равнобедренного треугольника
, так как ОМ — медиана равнобедренного треугольника 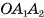 , проведенная к его основанию
, проведенная к его основанию 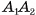 .
.
3)Так как 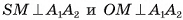 , то по признаку перпендикулярности прямой и плоскости прямая
, то по признаку перпендикулярности прямой и плоскости прямая 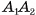 перпендикулярна плоскости SOM, а, значит,
перпендикулярна плоскости SOM, а, значит, 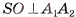 . Аналогично доказывается, что
. Аналогично доказывается, что 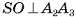 .
.
4)Таким образом, 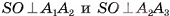 , следовательно, по признаку перпендикулярности прямой и плоскости прямая SO перпендикулярна плоскости основания пирамиды.
, следовательно, по признаку перпендикулярности прямой и плоскости прямая SO перпендикулярна плоскости основания пирамиды.
Теорема доказана.
Теорема 2 (о площади боковой поверхности правильной пирамиды). Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему 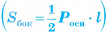 .
.
Доказательство.
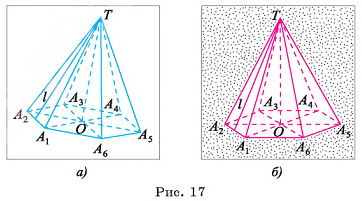
Пусть 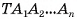 — правильная n-угольная пирамида (на рисунке 17, а, б изображена правильная шестиугольная пирамида),
— правильная n-угольная пирамида (на рисунке 17, а, б изображена правильная шестиугольная пирамида), 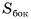 — площадь ее боковой поверхности,
— площадь ее боковой поверхности, 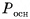 — периметр основания и l — ее апофема. Боковые грани правильной пирамиды являются равными равнобедренными треугольниками, основания которых — стороны основания пирамиды, а высоты равны апофеме I.
— периметр основания и l — ее апофема. Боковые грани правильной пирамиды являются равными равнобедренными треугольниками, основания которых — стороны основания пирамиды, а высоты равны апофеме I.
Площадь боковой поверхности пирамиды равна сумме площадей указанных равнобедренных треугольников, т. е.
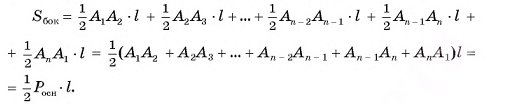
Теорема доказана.
Пример №4
Если в пирамиде все боковые ребра равны, то основание высоты пирамиды совпадает с центром окружности, описанной около многоугольника, служащего основанием пирамиды. Докажите.
Доказательство.
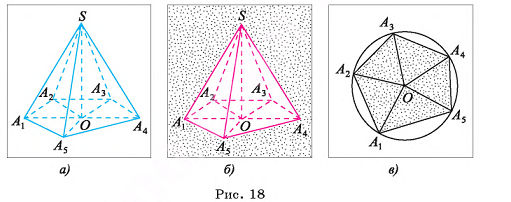
Пусть 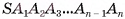 — правильная пирамида, у которой
— правильная пирамида, у которой 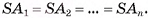 Точка О — основание высоты пирамиды (на рисунке 18, а, б изображена пятиугольная пирамида). Докажем, что точка О есть центр окружности, описанной около многоугольника
Точка О — основание высоты пирамиды (на рисунке 18, а, б изображена пятиугольная пирамида). Докажем, что точка О есть центр окружности, описанной около многоугольника 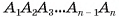 (рис. 18, в). Для этого достаточно доказать, что точка О равноудалена от вершин
(рис. 18, в). Для этого достаточно доказать, что точка О равноудалена от вершин 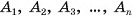 основания пирамиды. Отрезки
основания пирамиды. Отрезки 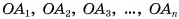 равны, так как являются проекциями равных наклонных
равны, так как являются проекциями равных наклонных 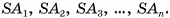 Следовательно, точка О является центром окружности, описанной около основания
Следовательно, точка О является центром окружности, описанной около основания 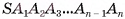 пирамиды.
пирамиды.
Пример №5
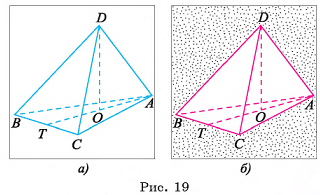
Основание пирамиды — равнобедренный треугольник, длина основания которого равна 6 см и высота 9 см. Вычислите высоту пирамиды, если длина каждого бокового ребра равна 13 см.
Дано:
DABC — пирамида,
DA = DB = DC = 13 см,
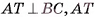 = 9 см,
= 9 см,
ВС = 6 см, АВ=АС
(рис. 19, а, б).
Найти: DO.
Решение:
1)Так как боковые ребра пирамиды равны, то основание высоты пирамиды совпадает с центром окружности, описанной около треугольника ABC. Высоту DO можно найти из прямоугольного треугольника AOD. Для этого достаточно найти АО.
2)В треугольнике ABC имеем: 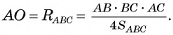
Значит, необходимо найти длину стороны АВ и площадь 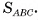
3)В треугольнике A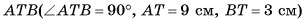 длина гипотенузы
длина гипотенузы 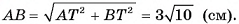
4)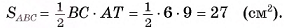 Таким образом,
Таким образом, 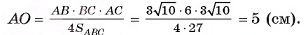
5) Из треугольника 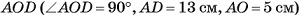 найдем длину катета
найдем длину катета 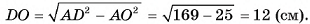
Ответ: 12 см.
Усеченная пирамида
Рассмотрим понятие усеченной пирамиды.
Определение. Пусть плоскость р параллельна плоскости а основания пирамиды 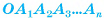 и пересекает ее боковые ребра
и пересекает ее боковые ребра 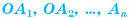 соответственно в точках
соответственно в точках 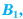
 (рис. 20, а). Многогранник, гранями которого являются два n-угольника
(рис. 20, а). Многогранник, гранями которого являются два n-угольника 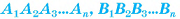 и n четырехугольников
и n четырехугольников 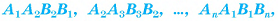 называется усеченной пирамидой (рис. 20, б, в).
называется усеченной пирамидой (рис. 20, б, в).
Отрезки 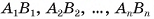 называются боковыми ребрами усеченной пирамиды.
называются боковыми ребрами усеченной пирамиды.
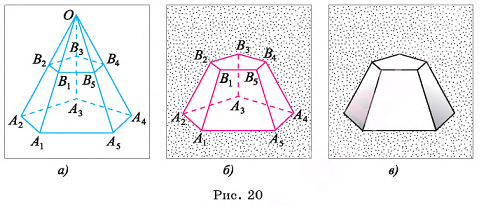
Два n-угольника 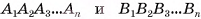 называются основаниями усеченной пирамиды, а четырехугольники
называются основаниями усеченной пирамиды, а четырехугольники 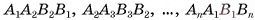 — ее боковыми гранями.
— ее боковыми гранями.
Усеченная пирамида с основаниями 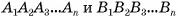 обозначается
обозначается 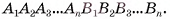
Высотой усеченной пирамиды, называется перпендикуляр (или длина этого перпендикуляра), проведенный из какой-нибудь точки плоскости одного основания к плоскости другого основания.
Боковые грани усеченной пирамиды являются трапециями.
Докажем, например, что четырехугольник 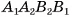 — трапеция. Стороны
— трапеция. Стороны 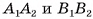 параллельны, так как лежат на прямых, по которым плоскость
параллельны, так как лежат на прямых, по которым плоскость 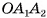 пересекает параллельные плоскости
пересекает параллельные плоскости 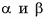 (см. рис 20, а). Прямые, на которых лежат стороны
(см. рис 20, а). Прямые, на которых лежат стороны 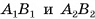 , пересекаются в точке О. Следовательно, четырехугольник
, пересекаются в точке О. Следовательно, четырехугольник 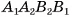 — трапеция. Аналогично можно доказать, что остальные боковые грани усеченной пирамиды — трапеции.
— трапеция. Аналогично можно доказать, что остальные боковые грани усеченной пирамиды — трапеции.
Усеченная пирамида называется правильной, если она является многогранником, который отсекается плоскостью, параллельной основанию правильной пирамиды.
Основания правильной усеченной пирамиды — правильные многоугольники.
Боковые грани правильной усеченной пирамиды — равнобедренные трапеции.
Апофемой правильной усеченной пирамиды называется высота ее боковой грани.
Площадью боковой поверхности усеченной пирамиды называется сумма площадей всех ее боковых граней.
Пример №6
Длины сторон оснований правильной усеченной четырехугольной пирамиды равны а и 2а, боковое ребро составляет с плоскостью основания угол ф. Найдите высоту пирамиды.
Дано:
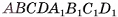 — правильная усеченная пирамида,
— правильная усеченная пирамида,
точки 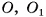 — центры ее оснований,
— центры ее оснований,
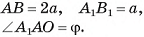
Найти: 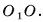
Решение:
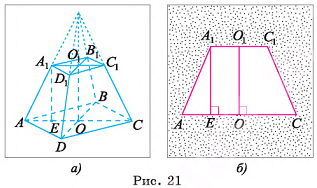
1)Отрезок 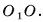 , лежит на высоте соответствующей неусеченной пирамиды (рис. 21, а), следовательно,
, лежит на высоте соответствующей неусеченной пирамиды (рис. 21, а), следовательно, 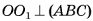 . Проведем
. Проведем 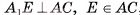 , тогда
, тогда 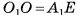 . Длину отрезка
. Длину отрезка 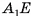 можно найти из треугольника
можно найти из треугольника 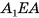 . Для этого достаточно найти
. Для этого достаточно найти 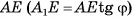 /
/
2)В треугольнике 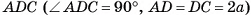 длина гипотенузы
длина гипотенузы 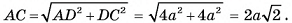
3)Из треугольника 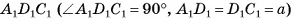
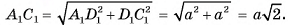
4)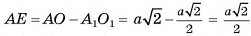 (рис. 21, 6).
(рис. 21, 6).
5)В треугольнике 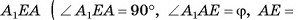
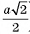 ), длина катета
), длина катета 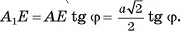
Ответ: 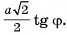
Многогранники
Пример №7
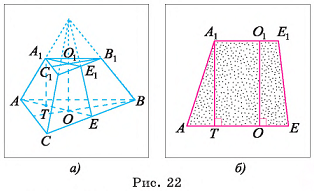
В правильной треугольной усеченной пирамиде длина стороны большего основания равна а, а длина стороны меньшего основания — b, боковое ребро образует с основанием острый угол ф. Найдите площадь сечения пирамиды плоскостью, проходящей через боковое ребро и центр нижнего основания.
Дано:
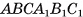 — правильная усеченная треугольная пирамида,
— правильная усеченная треугольная пирамида,
АС = а,
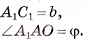
Найти: 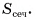
Решение:
1)Секущая плоскость, проходящая через ребро 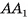 и центр О основания ABC, пересекает нижнее и верхнее основания по отрезкам
и центр О основания ABC, пересекает нижнее и верхнее основания по отрезкам 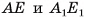 соответственно (точки
соответственно (точки 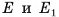 — середины отрезков
— середины отрезков 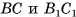 , соответственно). Четырехугольник
, соответственно). Четырехугольник 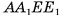 — искомое сечение (рис. 22, а, б).
— искомое сечение (рис. 22, а, б).
2)Сечение 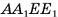 — трапеция (
— трапеция (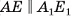 , отрезки
, отрезки 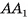 и
и 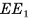 лежат на прямых, которые пересекаются). Проведем
лежат на прямых, которые пересекаются). Проведем
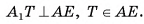 Тогда
Тогда 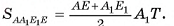
3)В треугольнике 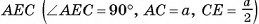 длина катета
длина катета 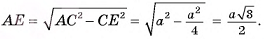
4)Из треугольника 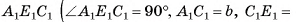
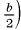 длина катета
длина катета 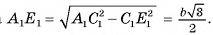
5) 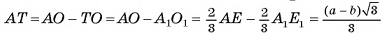 (точки
(точки 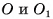 - центры оснований пирамиды)(см. рис. 22, а, б).
- центры оснований пирамиды)(см. рис. 22, а, б).
6) В треугольнике 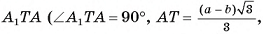
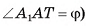 длина катета
длина катета 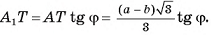
7) Теперь найдем площадь сечения 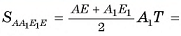
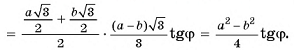
Ответ: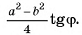
Решите самостоятельно следующую задачу.
Пример №8
Докажите, что площадь боковой поверхности 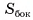 ; правильной усеченной пирамиды равна произведению полусуммы периметров ее оснований
; правильной усеченной пирамиды равна произведению полусуммы периметров ее оснований 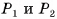 на апофему I, т. е.
на апофему I, т. е.
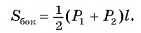
Правильные многогранники
Среди окружающих нас форм живой и неживой природы часто встречаются совершенные, удивляющие своей красотой благодаря присущей им симметрии. К их числу относятся и различные кристаллы, имеющие форму многогранников, в частности правильных многогранников. Прежде чем перейти к изучению вопросов о правильных многогранниках, напомним некоторые понятия.
Определение. Точки М и М, называются симметричными относительно точки О, если О является серединой отрезка ММ1.
Например, вершины А и 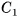 параллелепипеда
параллелепипеда 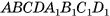 симметричны относительно точки О пересечения его диагоналей (рис. 28, а). Действительно,
симметричны относительно точки О пересечения его диагоналей (рис. 28, а). Действительно, 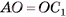 и так как диагонали параллелепипеда точкой пересечения делятся пополам.
и так как диагонали параллелепипеда точкой пересечения делятся пополам.
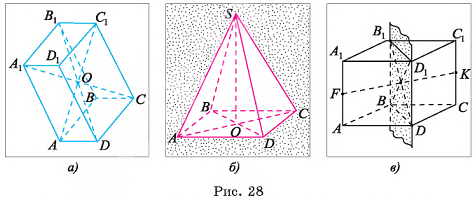
Определение. Точки М и M1 называются симметричными относительно прямой I, если прямая I проходит через середину отрезка МM1 и перпендикулярна ему.
Например, вершины В и D правильной четырехугольной пирамиды SABCD симметричны относительно прямой SO, где О — точка пересечения диагоналей основания пирамиды (рис. 28, б).
В самом деле, прямая SO перпендикулярна плоскости основания, а следовательно, и отрезку BD. Кроме того, точка О есть точка пересечения диагоналей квадрата ABCD, а значит, точка О — середина отрезка BD.
Определение. Точки М и М1 называются симметричными относительно плоскости а, если плоскость а проходит через середину отрезка МM1 и перпендикулярна этому отрезку.
Например, середины F и К соответственно ребер 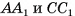 куба
куба 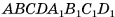 симметричны относительно плоскости, в которой лежит диагональное сечение
симметричны относительно плоскости, в которой лежит диагональное сечение 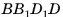 (рис. 28, в).
(рис. 28, в).
Определение. Точка О (прямая I, плоскость а) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно точки О (прямой I, плоскости а) некоторой точке этой же фигуры.
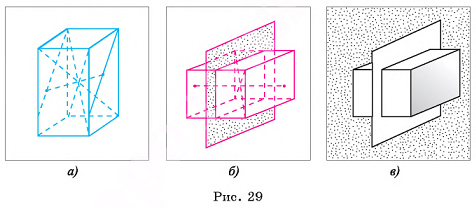
Например, точка пересечения диагоналей прямоугольного параллелепипеда является его центром симметрии (рис. 29, а).
Плоскость, проходящая через точку пересечения диагоналей прямоугольного параллелепипеда и параллельная какой-нибудь грани, есть одна из его плоскостей симметрии (рис. 29, б, в).
Определение. Выпуклый многогранник называется правильным, если все его грани — равные между собой правильные многоугольники и в каждой вершине сходится одно и то же число ребер.
Например, куб — правильный многогранник. Все грани куба — равные квадраты (правильные четырехугольники), а в каждой его вершине сходится три ребра.
Многогранник ABCD, вершинами которого являются концы двух скрещивающихся диагоналей противолежащих граней куба, является правильным (тетраэдр) (рис. 30, а, б, в).
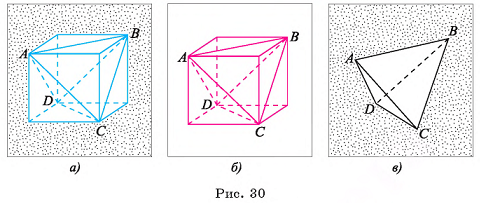
Каждая его грань — равносторонний треугольник, а в каждой вершине сходится три ребра.
Существует всего пять видов правильных многогранников. Для того чтобы установить это, заметим, что можно доказать следующее свойство: в выпуклом многограннике сумма градусных мер всех плоских углов при каждой вершине меньше 360°.
Можно доказать, что не существует правильного многогранника, гранями которого являются правильные n-угольники при 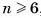 . Действительно, угол
. Действительно, угол 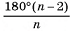 правильного n-угольника при
правильного n-угольника при 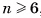 не меньше 120°. Если бы существо-ват правильный многогранник, гранями которого являются правильные n-угольники при
не меньше 120°. Если бы существо-ват правильный многогранник, гранями которого являются правильные n-угольники при 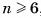 , то сумма градусных мер всех плоских углов при каждой вершине была бы не меньше 360° (при каждой вершине многогранника не меньше трех плоских углов), а это противоречит сформулированному свойству плоских углов при вершине выпуклого многогранника.
, то сумма градусных мер всех плоских углов при каждой вершине была бы не меньше 360° (при каждой вершине многогранника не меньше трех плоских углов), а это противоречит сформулированному свойству плоских углов при вершине выпуклого многогранника.
Каждая вершина правильного многогранника может быть вершиной: а) трех, четырех или пяти равносторонних треугольников; б) трех квадратов; в) трех правильных пятиугольников .
Таким образом, существуют следующие виды правильных многогранников: тетраэдр, куб, октаэдр, икосаэдр, додекаэдр.
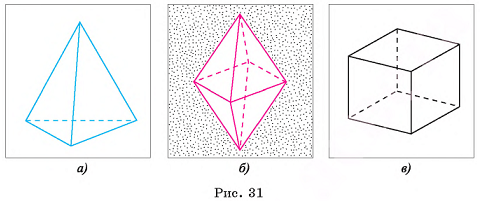
Поверхность тетраэдра (рис. 31, а) образована четырьмя равносторонними треугольниками, а каждая его вершина является вершиной трех треугольников.
Поверхность октаэдра (рис. 31, б) состоит из восьми равносторонних треугольников, а каждая его вершина является вершиной четырех треугольников.
Поверхность куба (рис. 31, в) образована шестью равными квадратами. Каждая вершина куба является вершиной трех квадратов.
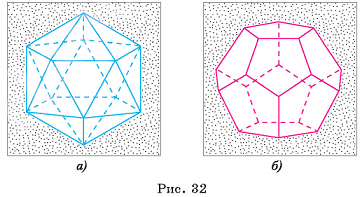
Поверхность икосаэдра (рис. 32, а) составлена из двадцати равных равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти равносторонних треугольников.
Поверхность додекаэдра (рис. 32, б) составлена из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников.
В переводе с греческого названия тетраэдр, октаэдр, додекаэдр, икосаэдр означают соответственно четырехгранник, восьмигранник, двенадцатигранник, двадцатигранник.
Факт существования пяти правильных многогранников был установлен еще во времена древних греков. Впервые исследованные пифагорейцами, эти пять правильных многогранников были впоследствии описаны Платоном и стали называться Платоновыми телами.
Каждый правильный многогранник обладает определенными элементами симметрии. Например, прямая, проходящая через середины противолежащих ребер тетраэдра, является его осью симметрии.
Можно доказать, что тетраэдр имеет три оси симметрии.
Плоскостью симметрии для тетраэдра является плоскость, проходящая через некоторое ребро и перпендикулярная противолежащему ребру. Тетраэдр имеет шесть плоскостей симметрии.
Например, если DABC — тетраэдр, а точка F — середина ребра ВС, тогда плоскость ADF есть плоскость симметрии тетраэдра DABC. Действительно, при симметрии относительно плоскости ADF образами вершин А и D являются соответственно вершины А и D, так как они лежат в плоскости ADF, а значит, каждая из них отображается сама в себя. Вершины С и В при симметрии относительно плоскости ADF отображаются одна в другую, так как 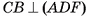 и CF = FB. Следовательно, при симметрии относительно плоскости ADF образом тетраэдра DABC является сам этот тетраэдр, т. е. он симметричен относительно плоскости ADF (рис. 33, а).
и CF = FB. Следовательно, при симметрии относительно плоскости ADF образом тетраэдра DABC является сам этот тетраэдр, т. е. он симметричен относительно плоскости ADF (рис. 33, а).
Можно доказать, что куб имеет центр симметрии, которым является точка пересечения его диагоналей. Осями симметрии куба являются прямые, проходящие через центры противолежащих граней, а также прямые, проходящие через середины противолежащих ребер куба. Таким образом, куб имеет всего девять осей симметрии. Плоскостей симметрии у куба также всего девять.
Форму куба имеют кристаллы поваренной соли, а кристаллы пирита имеют форму правильных додекаэдров. Благодаря элементам симметрии правильные многогранники обладают особенной красотой, а их свойства находят применение в архитектуре и строительстве, используются приизучении структур различных веществ, так как симметрия правильных многогранников проявляется в атомных структурах молекул и кристаллов.
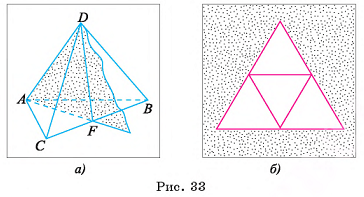
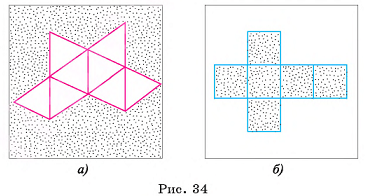
Модели поверхностей правильных многогранников можно склеить из плотной бумаги или картона, воспользовавшись для этого развертками этих многогранников. На рисунке 33, б изображена развертка тетраэдра, а на рисунках 34, а и 34, б изображены соответственно развертки октаэдра и куба. Перечертив эти развертки на лист плотной бумаги в большем масштабе и сделав необходимые припуски для склеивания, вы можете склеить модели поверхностей соответствующих правильных многогранников.
Объемы многогранников
Из курса планиметрии известно понятие площади многоугольника.
Площадь — это положительная величина, определенная для каждого многоугольника, числовое значение которой обладает свойствами:
- равные многоугольники имеют равные площади;
- если многоугольник есть объединение конечного числа многоугольников, каждые два из которых не имеют общих внутренних точек, то его площадь равна сумме площадей этих многоугольников;
- площадь квадрата, сторона которого равна единице измерения длины, равна единице.
Каждый многоугольник имеет площадь, которая измеряется с помощью выбранной единицы площади, т. е. площади квадрата, стороной которого служит единица измерения длины. Площадь может измеряться в квадратных сантиметрах (см2), в квадратных метрах (м2), в квадратных километрах (км2) и т. д.
Аналогично для многогранников в пространстве вводится понятие объема.
Объем — это положительная величина, определенная для каждого из многогранников, числовое значение которой имеет следующие свойства:
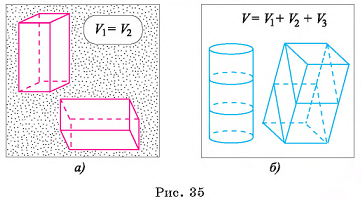
- а) равные многогранники имеют равные объемы (рис. 35, а);
- б) если многогранник есть объединение конечного числа многогранников, каждые два из которых не имеют общих внутренних точек, то его объем равен сумме объемов этих многогранников (рис. 35, б);
- в) объем куба, ребро которого равно единице измерения длины, равен единице.
Объем многогранников измеряется с помощью выбранной единицы объема, т. е. объема куба, ребром которого служит единица измерения длины.
На практике объем измеряется в различных единицах измерения: в кубических сантиметрах (см3), в кубических метрах (м3), в кубических километрах (км3) и т. д.
Заметим, что из определения объема многогранников еще не следует существование объема для каждого многогранника и его единственность. Необходимо доказать, во-первых, что на множестве многогранников существует положительная величина, обладающая указанными свойствами, и, во-вторых, что такая величина единственная. Доказательство существования и единственности функции объема на множестве многогранников здесь не рассматривается по причине его громоздкости в рамках школьного курса. Далее мы изучим вопрос о нахождении объемов некоторых многогранников.
В практической деятельности человек часто встречается с необходимостью вычисления объемов, например при изготовлении каких-либо деталей или при строительстве различных сооружений. Многие строительные объекты и детали конструкций имеют форму геометрических тел: параллелепипедов, призм, пирамид и т. д., поэтому представляет интерес вопрос о том, как вычислять объемы многогранников, выражая их через другие величины, характеризующие эти многогранники.
В дальнейшем мы познакомимся с правилами вычисления объемов призмы и пирамиды, а сейчас рассмотрим вопрос вычисления объема прямоугольного параллелепипеда.
Теорема (об объеме прямоугольного параллелепипеда).
Объем прямоугольного параллелепипеда равен произведению трех его измерений, т. е. если V — объем прямоугольного параллелепипеда, а а, b, с — его измерения, то V = аbс.
Доказательство.
Возможны три случая длин ребер прямоугольного параллелепипеда.
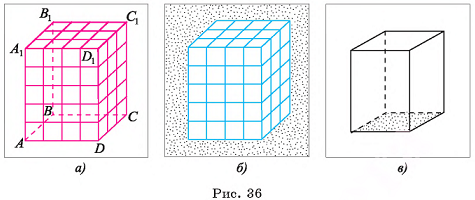
1)Пусть длины ребер прямоугольного параллелепипеда 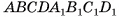 (рис. 36, а, б) — натуральные числа а, b, с
(рис. 36, а, б) — натуральные числа а, b, с 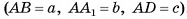 . Разделим ребра
. Разделим ребра 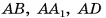 соответственно на а, b, с равных частей. Через точки деления проведем плоскости, параллельные граням
соответственно на а, b, с равных частей. Через точки деления проведем плоскости, параллельные граням 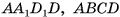
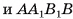 соответственно. Тогда данный параллелепипед разбивается на
соответственно. Тогда данный параллелепипед разбивается на 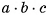 кубиков, у каждого из которых длина ребра равна 1. Значит, данный параллелепипед разбит на
кубиков, у каждого из которых длина ребра равна 1. Значит, данный параллелепипед разбит на 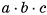 кубов единичного объема.
кубов единичного объема.
По второму свойству объемов объем параллелепипеда равен 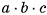 .
.
2)Пусть длины ребер прямоугольного параллелепипеда есть рациональные числа. Не нарушая общности, можем считать, что 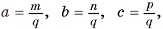 где
где 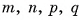 есть натуральные числа. Разобьем данный параллелепипед на единичные кубы, длина ребра каждого из которых равна
есть натуральные числа. Разобьем данный параллелепипед на единичные кубы, длина ребра каждого из которых равна 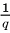 . Параллелепипед содержит
. Параллелепипед содержит 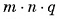 таких кубов, объем каждого из которых равен
таких кубов, объем каждого из которых равен 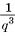 . Следовательно, объем параллелепипеда равен
. Следовательно, объем параллелепипеда равен 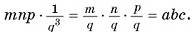
3)Можно доказать, что эта теорема верна и для случая, когда длина хотя бы одного из ребер есть число иррациональное.
Следствие. Объем прямоугольного параллелепипеда равен произведению площади его основания на высоту (рис. 36, в).
Объем наклонного параллелепипеда
Рассмотрим вопрос о вычислении объема наклонного параллелепипеда, но прежде докажем следующую теорему.
Теорема 1 (об объеме прямого параллелепипеда).
Объем прямого параллелепипеда равен произведению площади его основания на высоту 
Доказательство.
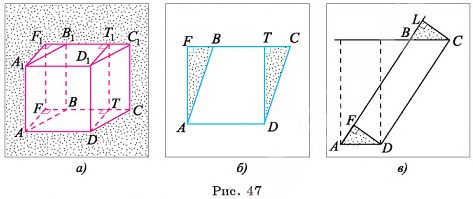
1)Пусть 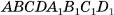 — прямой параллелепипед, основание которого — параллелограмм ABCD площадью
— прямой параллелепипед, основание которого — параллелограмм ABCD площадью  , а высота параллелепипеда AAl = h. Докажем, что объем параллелепипеда
, а высота параллелепипеда AAl = h. Докажем, что объем параллелепипеда  . Проведем высоты DT и AF параллелограмма ABCD и
. Проведем высоты DT и AF параллелограмма ABCD и 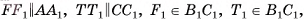
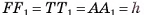 (рис. 47, а, б).
(рис. 47, а, б).
2)Прямой параллелепипед 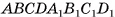 составлен из прямой четырехугольной призмы
составлен из прямой четырехугольной призмы 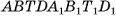 и треугольной призмы
и треугольной призмы 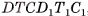 , а прямоугольный параллелепипед
, а прямоугольный параллелепипед 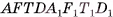 составлен из той же призмы
составлен из той же призмы 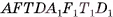 и треугольной призмы
и треугольной призмы 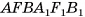 .
.
Призмы 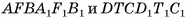 равны, так как их можно совместить, а значит, равны объемы этих призм. Таким образом, объем V прямого параллелепипеда
равны, так как их можно совместить, а значит, равны объемы этих призм. Таким образом, объем V прямого параллелепипеда 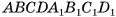 , равен объему V1 прямоугольного параллелепипеда
, равен объему V1 прямоугольного параллелепипеда 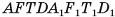 (см. рис. 47, a).
(см. рис. 47, a).
3)По теореме предыдущего параграфа объем 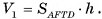 Следовательно,
Следовательно, 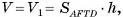 а так как
а так как 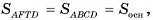 то
то 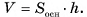
Замечание. В случае, когда основание параллелепипеда — параллелограмм ABCD, показанный на рисунке 47, в, проведем высоты DF, CL и 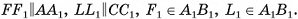 Рассмотрим равные треугольные призмы
Рассмотрим равные треугольные призмы 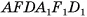 и
и 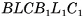 . В остальном доказательство аналогично.
. В остальном доказательство аналогично.
Теорема доказана.
Теорема 2 (об объеме наклонного параллелепипеда).
Объем наклонного параллелепипеда равен произведению площади основания на высоту параллелепипеда 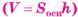 .
.
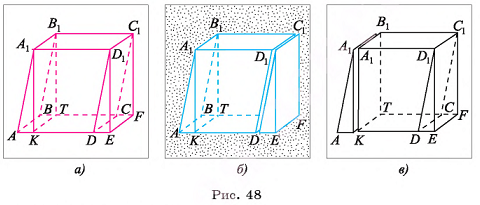
Доказательство:
1. Сначала докажем теорему для параллелепипеда, у которого две противолежащие боковые грани перпендикулярны плоскости основания, а затем — для произвольного параллелепипеда.
1)Пусть 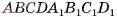 — параллелепипед, у которого боковые грани
— параллелепипед, у которого боковые грани 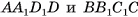 перпендикулярны плоскости основания, объем равен V, площадь основания —
перпендикулярны плоскости основания, объем равен V, площадь основания — 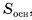 , а его высота — h. Проведем отрезки
, а его высота — h. Проведем отрезки 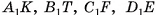 перпендикулярно плоскости основания (рис. 48, а). Тогда
перпендикулярно плоскости основания (рис. 48, а). Тогда 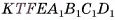 — прямой параллелепипед.
— прямой параллелепипед.
2)Геометрическое тело 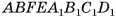 составлено из данного параллелепипеда
составлено из данного параллелепипеда 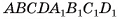 и призмы
и призмы 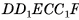 (основание призмы — треугольник
(основание призмы — треугольник 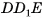 ), кроме того, оно составлено из прямого параллелепипеда
), кроме того, оно составлено из прямого параллелепипеда 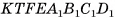 и призмы
и призмы 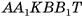 (основание призмы — треугольник
(основание призмы — треугольник 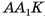 ) (рис. 48, б, в).
) (рис. 48, б, в).
3)Призмы 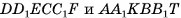 равны (их можно совместить, если совместить равные основания
равны (их можно совместить, если совместить равные основания 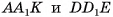 и равные ребра КТ и EF), а значит, равны объемы этих призм.
и равные ребра КТ и EF), а значит, равны объемы этих призм.
Таким образом, объем V данного параллелепипеда 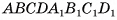 равен объему V1 прямого параллелепипеда
равен объему V1 прямого параллелепипеда 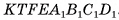 . По предыдущей теореме объем
. По предыдущей теореме объем 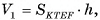 а так как
а так как 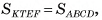 то
то 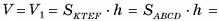
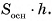
2. Докажем теорему для произвольного параллелепипеда.
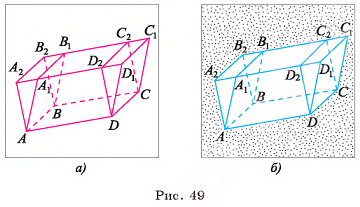
Через ребра АВ и DC основания ABCD наклонного параллелепипеда 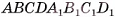 проведем плоскости, перпендикулярные плоскости основания. Пусть они пересекают параллельные прямые
проведем плоскости, перпендикулярные плоскости основания. Пусть они пересекают параллельные прямые 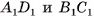 в точках
в точках 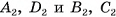 соответственно (рис. 49, а, б). Тогда противолежащие боковые грани
соответственно (рис. 49, а, б). Тогда противолежащие боковые грани 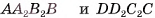 полученного параллелепипеда
полученного параллелепипеда 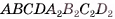 перпендикулярны плоскости его основания. Объем V данного параллелепипеда
перпендикулярны плоскости его основания. Объем V данного параллелепипеда 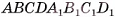 равен объему V1 параллелепипеда
равен объему V1 параллелепипеда 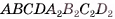 . По доказанному
. По доказанному 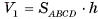 , следовательно,
, следовательно, 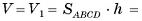
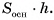
Теорема доказана.
Пример №9
Основание прямого параллелепипеда 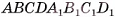 — ромб ABCD, площадь которого равна 12 см2, а длина диагонали BD основания равна 4 см. Вычислите объем параллелепипеда, если диагональ АС1 наклонена к основанию под углом 45°.
— ромб ABCD, площадь которого равна 12 см2, а длина диагонали BD основания равна 4 см. Вычислите объем параллелепипеда, если диагональ АС1 наклонена к основанию под углом 45°.
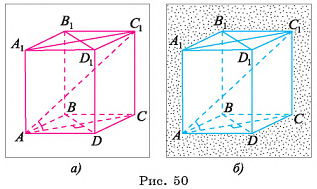
Дано:
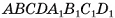 — прямой параллелепипед,
— прямой параллелепипед,
ABCD — ромб,
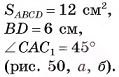
Найти: V.
Решение:
1)Объем прямого параллелепипеда равен произведению площади основания на высоту 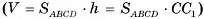 . Следовательно, для нахождения объема параллелепипеда достаточно найти длину бокового ребра СС1.
. Следовательно, для нахождения объема параллелепипеда достаточно найти длину бокового ребра СС1.
2)Основание параллелепипеда — ромб, значит, его площадь 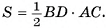 Из равенства
Из равенства 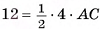 найдем АС = 6 см.
найдем АС = 6 см.
3)Так как данный параллелепипед прямой, a 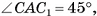 то АС = СС1 = 6 см.
то АС = СС1 = 6 см.
4)Теперь найдем объем параллелепипеда: 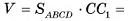 12 -б =72 см3.
12 -б =72 см3.
Ответ: 72 см3.
Объем призмы
В предыдущем параграфе рассматривалась формула, позволяющая находить объем параллелепипеда — многогранника, являющегося частным примером призмы (параллелепипед есть призма, основание которой — параллелограмм). Теперь найдем формулу для вычисления произвольной призмы.
Теорема (об объеме призмы).
Объем призмы равен произведению площади основания на высоту 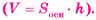
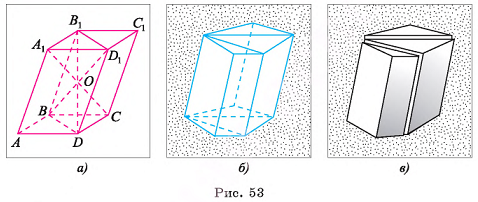
Доказательство:
1. Сначала докажем, эту теорему для произвольной треугольной призмы 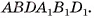
Рассмотрим в пространстве точки С и С1 такие, что ABCD — параллелограмм, а 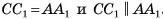 . Тогда параллелепипед
. Тогда параллелепипед 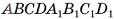 диагональным сечением BB{D{D делится на две призмы
диагональным сечением BB{D{D делится на две призмы 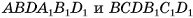 (рис. 53, а). Эти призмы имеют равные объемы, так как они симметричны относительно точки О пересечения диагоналей параллелепипеда
(рис. 53, а). Эти призмы имеют равные объемы, так как они симметричны относительно точки О пересечения диагоналей параллелепипеда 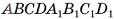 . Таким образом, объем построенного параллелепипеда равен удвоенному объему данной призмы.
. Таким образом, объем построенного параллелепипеда равен удвоенному объему данной призмы.
Объем V0 параллелепипеда равен произведению площади основания на высоту. Площадь основания параллелепипеда равна удвоенной площади треугольника ABD, а его высота равна высоте h данной призмы. Следовательно, объем V данной призмы равен произведению площади ее основания на высоту:
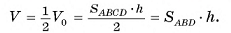
2. Докажем теорему для произвольной призмы.
Пусть дана произвольная призма, высота которой h, а площадь основания 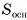 . Такую призму можно разбить на треугольные призмы с высотой h (на рисунке 53, б, в для определенности показано разбиение пятиугольной призмы на три треугольные). В общем случае n-угольную призму можно разбить на (n - 2) треугольные призмы. Объем данной призмы равен сумме объемов треугольных призм, составляющих ее. По доказанному объем треугольной призмы равен произведению площади ее основания на высоту. Следовательно, объем данной призмы
. Такую призму можно разбить на треугольные призмы с высотой h (на рисунке 53, б, в для определенности показано разбиение пятиугольной призмы на три треугольные). В общем случае n-угольную призму можно разбить на (n - 2) треугольные призмы. Объем данной призмы равен сумме объемов треугольных призм, составляющих ее. По доказанному объем треугольной призмы равен произведению площади ее основания на высоту. Следовательно, объем данной призмы
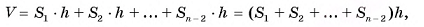
где 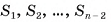 — площади треугольников, на которые разбито основание призмы. Сумма площадей треугольников равна площади
— площади треугольников, на которые разбито основание призмы. Сумма площадей треугольников равна площади 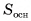 основания данной призмы, значит,
основания данной призмы, значит, 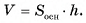
Теорема доказана.
Следствие. Объем прямой призмы равен произведению площади основания на длину бокового ребра.
Пример №10
Основание прямой призмы — равносторонний треугольник, длина стороны которого равна а. Сечение, проведенное через сторону одного основания и противолежащую вершину другого основания, составляет с основанием призмы угол 30°. Найдите объем призмы.
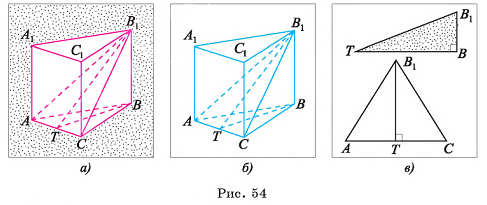
Решение:
1) Объем V призмы равен произведению площади основания на высоту призмы: 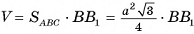 (рис. 54, а, б).
(рис. 54, а, б).
2)Пусть точка Т — середина отрезка АС, тогда 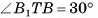
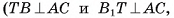 следовательно,
следовательно, 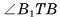 — линейный угол двугранного угла
— линейный угол двугранного угла 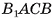 ). В прямоугольном треугольнике ВТС
). В прямоугольном треугольнике ВТС 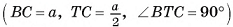
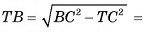
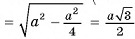 (Рис. 54, а, б, в).
(Рис. 54, а, б, в).
3)Из прямоугольного треугольника 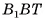
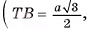
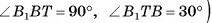 длина катета
длина катета 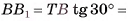
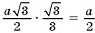 (рис. 54 а б в)
(рис. 54 а б в)
4)Таким образом, объем призмы 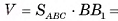
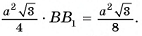
Ответ: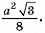
Объем пирамиды
Рассмотрим вопрос о нахождении объема треугольной и произвольной пирамиды. Предварительно докажем следующую теорему.
Теорема 1 (об объеме пирамид, имеющих равные высоты и равные площади основании).
Две треугольные пирамиды, имеющие равные высоты и равные площади оснований, имеют равные объемы.
Доказательство:
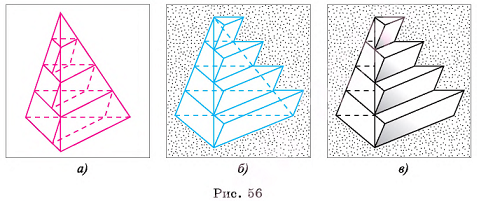
1)Пусть даны две пирамиды, имеющие равные высоты и равные площади оснований. Разделим высоту каждой из пирамид на п равных частей и проведем через точки деления плоскости, параллельные их основаниям. Указанные плоскости разбивают каждую пирамиду на п частей. Для каждой части первой пирамиды построим призму, которая расположена в этой части, как показано на рисунке 56, а (основание призмы совпадает с треугольником сечения, а боковое ребро параллельно боковому ребру пирамиды). Для каждой части другой пирамиды построим призму, которая содержит эту часть, как показано на рисунке 56, б, в.
2) Призма, содержащаяся во 2-й части первой пирамиды (считая от вершины), и призма, которая содержит 1-ю часть второй пирамиды, имеют равные площади оснований так как их основания подобны основаниям пирамид с коэффициентом подобия 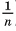 ). Кроме того, эти призмы имеют
). Кроме того, эти призмы имеют
равные высоты, следовательно, их объемы равны. Призма, содержащаяся в 3-й части первой пирамиды, и призма, которая содержит 2-ю часть другой пирамиды, имеют равные площади оснований (их основания подобны основаниям пирамиды с коэффициентом подобия 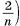 . Эти призмы также имеют равные высоты, значит, их объемы равны.
. Эти призмы также имеют равные высоты, значит, их объемы равны.
Аналогично призма, содержащаяся в к-й части первой пирамиды (считая от вершины), и призма, которая содержит (к - 1)-ю часть второй пирамиды, имеют равные площади оснований (так как эти основания подобны основаниям пирамид и коэффициент подобия один и тот же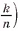 . Так как эти призмы имеют, кроме того, и равные высоты, то их объемы равны.
. Так как эти призмы имеют, кроме того, и равные высоты, то их объемы равны.
3) Пусть 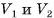 — объемы первой и второй пирамид, a
— объемы первой и второй пирамид, a 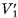 и
и 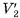 — суммы объемов построенных для них призм. Так как объем призмы в k-й части первой пирамиды равен объему призмы (к-1)-й части второй пирамиды, то сумма объемов всех призм первой пирамиды равна сумме объемов призм всех частей второй пирамиды, кроме объема
— суммы объемов построенных для них призм. Так как объем призмы в k-й части первой пирамиды равен объему призмы (к-1)-й части второй пирамиды, то сумма объемов всех призм первой пирамиды равна сумме объемов призм всех частей второй пирамиды, кроме объема 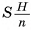 (S — площадь основания пирамиды, Н — ее высота) последней призмы (считая от вершины пирамиды). Следовательно,
(S — площадь основания пирамиды, Н — ее высота) последней призмы (считая от вершины пирамиды). Следовательно, 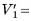
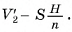 Так как
Так как 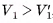 , то
, то 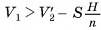 ; так как
; так как 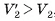 , то
, то 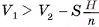 , т. е. данное неравенство выполняется при сколь угодно большом n, что возможно только при условии
, т. е. данное неравенство выполняется при сколь угодно большом n, что возможно только при условии 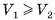 . Аналогично рассуждая, поменяв ролями пирамиды, приходим к неравенству
. Аналогично рассуждая, поменяв ролями пирамиды, приходим к неравенству 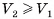 . Следовательно,
. Следовательно, 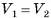 .
.
Теорема доказана.
Теорема 2 (об объеме треугольной пирамиды).
Объем любой треугольной пирамиды, равен одной третьей произведения площади ее основания на высоту 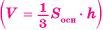 .
.
Доказательство:
1) Пусть дана треугольная пирамида ОABC, вершина которой — точка О, а основание — треугольник ABC, 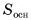 — площадь основания, h — высота пирамиды. Дополним данную пирамиду до призмы с тем же основанием и высотой. Эта
— площадь основания, h — высота пирамиды. Дополним данную пирамиду до призмы с тем же основанием и высотой. Эта
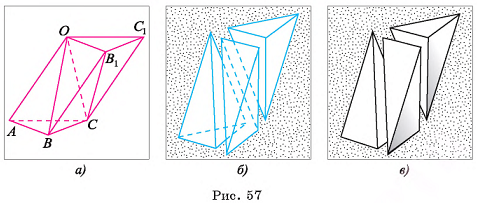
призма состоит из трех пирамид 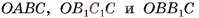 (рис. 57, а, б, в).
(рис. 57, а, б, в).
2)Пирамиды 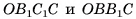 имеют равные основания
имеют равные основания 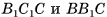 и общую высоту, проведенную из вершины О, следовательно, по теореме 1 они имеют равные объемы.
и общую высоту, проведенную из вершины О, следовательно, по теореме 1 они имеют равные объемы.
3)Пирамиды СОАВ и СОВВ1 также имеют равные основания ОАВ и ОВВ1 и равные высоты, проведенные из вершины С. Значит, по теореме 1 эти пирамиды также имеют равные объемы. Таким образом, все три пирамиды имеют равные объемы. Так как сумма этих объемов равна объему призмы, то объем V пирамиды равен одной третьей объема призмы, т. е. 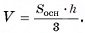
Теорема доказана.
Теорема 3 (об объеме n-угольной пирамиды).
Объем n-угольной пирамиды равен одной третьей произведения площади ее основания на высоту 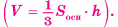
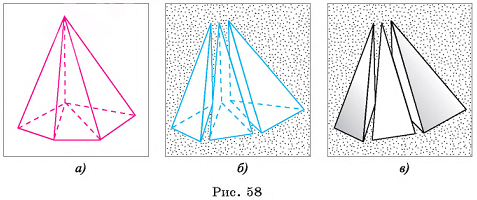
Доказательство:
Пусть дана n-угольная пирамида, площадь основания которой  , а высота равна h. Разобьем основание пирамиды на (n - 2) треугольника, проведя диагонали, выходящие из одной вершины. Пирамиды, основаниями которых являются эти треугольники, а вершиной является вершина данной пирамиды, составляют эту пирамиду (на рисунке 58, а, б, в показано разбиение для пятиугольной пирамиды). Так как эти пирамиды имеют одну и ту же высоту, то объем исходной пирамиды равен сумме объемов пирамид, на которые она разбита, т. е. ее объем равен:
, а высота равна h. Разобьем основание пирамиды на (n - 2) треугольника, проведя диагонали, выходящие из одной вершины. Пирамиды, основаниями которых являются эти треугольники, а вершиной является вершина данной пирамиды, составляют эту пирамиду (на рисунке 58, а, б, в показано разбиение для пятиугольной пирамиды). Так как эти пирамиды имеют одну и ту же высоту, то объем исходной пирамиды равен сумме объемов пирамид, на которые она разбита, т. е. ее объем равен:
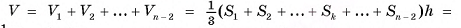
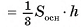 (Sk — площадь основания k-й пирамиды, на которые разбита данная пирамида).
(Sk — площадь основания k-й пирамиды, на которые разбита данная пирамида).
Теорема доказана.
Пример №11
Докажите, что объем V усеченной пирамиды вычисляется по формуле 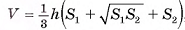 где S1, S2 — площади оснований, h — высота усеченной пирамиды.
где S1, S2 — площади оснований, h — высота усеченной пирамиды.
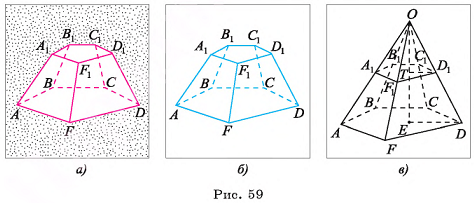
Доказательство:
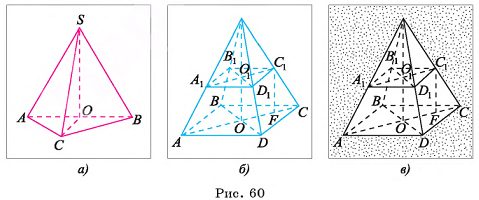
Пусть дана усеченная пирамида, например, для определенности, пятиугольная пирамида 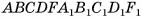 (рис. 59, а, б). Рассмотрим пирамиду
(рис. 59, а, б). Рассмотрим пирамиду 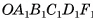 , которая дополняет данную усеченную пирамиду до пирамиды OABCDF (рис. 59, в). Тогда объем V усеченной пирамиды есть разность объемов пирамиды OABCDF и пирамиды
, которая дополняет данную усеченную пирамиду до пирамиды OABCDF (рис. 59, в). Тогда объем V усеченной пирамиды есть разность объемов пирамиды OABCDF и пирамиды 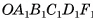 .
.
Пусть ТЕ = h — высота усеченной пирамиды, ТО = х — высота пирамиды 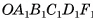 .
.
Тогда
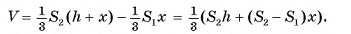
Многоугольники оснований усеченной пирамиды подобны (объясните почему), следовательно, их площади относятся как квадраты длин соответствующих сторон, т. е.
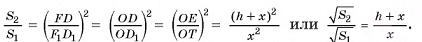
Из этого уравнения найдем 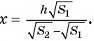 Таким образом, объем усеченной пирамиды равен:
Таким образом, объем усеченной пирамиды равен:
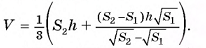
Так как 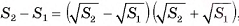 , то
, то
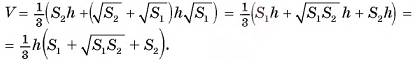
Теорема доказана.
Пример №12
Основание пирамиды — прямоугольный треугольник, длины катетов которого 6 см и 8 см. Длина каждого из боковых ребер пирамиды равна 13 см. Вычислите объем пирамиды.
Решение:
1) Пусть SABC — данная пирамида, АС = 6 см, ВС = 8 см, 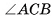 = 90°, AS = BS = CS = 13 см (рис. 60, а).
= 90°, AS = BS = CS = 13 см (рис. 60, а).
2)Пусть точка О — основание высоты пирамиды. Так как по условию AS = BS = CS, то АО = ВО = СО (проекции равных наклонных, которые проведены из одной точки, равны). Таким образом, точка О есть центр окружности, описанной около треугольника АСВ, т. е. точка О — середина гипотенузы AJB.
3)Объем пирамиды можем найти по формуле
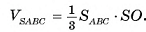
4)Площадь основания пирамиды равна:
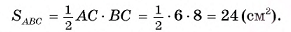
5)В треугольнике SOB 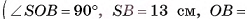
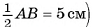 длина катета SO=
длина катета SO= 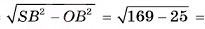 12 (см).
12 (см).
6)Таким образом, 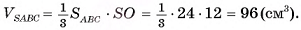
Ответ: 96 см3.
Пример №13
Вычислите объем правильной усеченной четырехугольной пирамиды, длины оснований которой равны 2 см и 4 см, а боковые ребра наклонены к основанию под углом 45°.
Решение:
1)Объем усеченной пирамиды можем найти по формуле
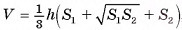 , где S1 и S2 — площади оснований пирамиды, h — ее высота.
, где S1 и S2 — площади оснований пирамиды, h — ее высота.
2)Основания данной пирамиды — квадраты, следовательно, их площади S1 = 16 см2 и S2 = 4 см2.
3)Пусть 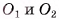 — центры оснований пирамиды. Отрезок
— центры оснований пирамиды. Отрезок 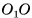 лежит на высоте соответствующей неусеченной пирамиды, а, значит,
лежит на высоте соответствующей неусеченной пирамиды, а, значит, 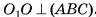 . Пусть
. Пусть 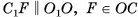 , тогда
, тогда 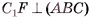 , а, следовательно,
, а, следовательно, 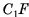 (рис. 60, б, в).
(рис. 60, б, в).
4)Найдем высоту пирамиды. Прямоугольный треугольник 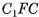 — равнобедренный, так как
— равнобедренный, так как 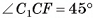 , следовательно,
, следовательно, 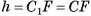 . Заметим, что
. Заметим, что 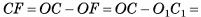
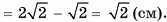
5)Теперь найдем объем пирамиды: 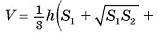
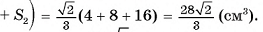
Ответ: 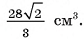
Многогранники и тела вращения
Сфера и шар
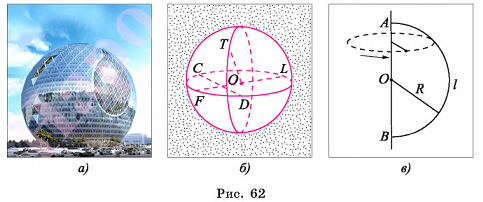
Рассмотрим понятия сферы и шара в пространстве, которые аналогичны понятиям окружности и круга на плоскости. Теннисный шарик и футбольный мяч дают представление о сфере, а шарик в шарикоподшипнике — о шаре. Форму шара и сферы имеют многие украшения и элементы архитектурных сооружений (рис. 62, а).
Определение. Сферой называется геометрическая фигура, состоящая из всех точек пространства, находящихся на заданном расстоянии от данной точки пространства.
Данная точка называется центром сферы.
Радиусом сферы называется отрезок, соединяющий центр сферы с какой-либо точкой сферы.
Иногда радиусом сферы называют длину отрезка, соединяющего центр сферы с какой-либо точкой сферы.
Из определения следует, что все радиусы сферы равны.
На рисунке 62, б изображены сфера с центром в точке О и радиусы OF и ОТ этой сферы.
Сфера с центром в точке О и радиусом R обозначается S(0, R) (читают: «Сфера с центром в точке О и радиусом R»).
Хордой сферы называется отрезок, соединяющий две точки сферы.
Диаметром сферы называется хорда, проходящая через ее центр.
Центр сферы делит любой его диаметр на два равных отрезка. Любой диаметр сферы радиусом R равен 2R.
Например, на рисунке 62, б изображены хорда CD и диаметр FL сферы с центром в точке О.
Заметим, что сферу радиусом R можно представить как поверхность, которую опишет полуокружность радиусом R при ее повороте на 360° около прямой, содержащей диаметр АВ этой полуокружности (рис. 62, в).
Определение. Шаром называется геометрическое тело, состоящее из сферы и части пространства, ограниченного этой сферой.
Другими словами, шар с центром в точке О и радиусом R представляет собой геометрическое тело, границей которого является сфера S(0, R).
Радиусом, хордой и диаметром шара называются радиус, хорда и диаметр сферы, которая является границей шара.
Заметим, что шар радиусом R можно представить как тело, которое опишет полукруг радиусом R при повороте этого полукруга на 360° около прямой, содержащей диаметр полукруга.
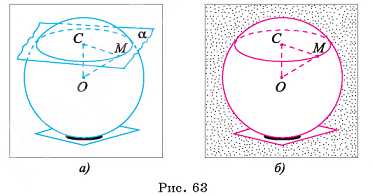
Теорема 1 (о сечении сферы плоскостью).
Сечение сферы, плоскостью есть окружность.
Доказательство:
Пусть плоскость а пересекает сферу S(0, R) и не проходит через ее центр. Из центра О опустим перпендикуляр ОС на плоскость а (рис. 63, а, б). Пусть ОС = d. Докажем, что пересечение сферы S(0, R) и плоскости а есть окружность с центром в точке С и радиусом 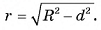
Пусть М — произвольная точка линии пересечения сферы S(0, R) и плоскости а. Докажем, что точка М принадлежит окружности с центром в точке С и радиусом 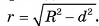 . Так как
. Так как 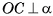 , то прямая ОС перпендикулярна каждой прямой плоскости а, а, значит,
, то прямая ОС перпендикулярна каждой прямой плоскости а, а, значит, 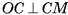 . В прямоугольном треугольнике
. В прямоугольном треугольнике 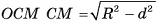 , т. е. точка М находится на расстоянии
, т. е. точка М находится на расстоянии 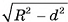 от точки С. Значит, она принадлежит окружности с центром в точке С и радиусом
от точки С. Значит, она принадлежит окружности с центром в точке С и радиусом 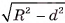 .
.
Пусть теперь точка М принадлежит окружности с центром в точке С и радиусом 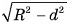 , расположенной в плоскости а. Докажем, что точка М — общая точка плоскости а и сферы S(0, R). Для этого достаточно доказать, что ОМ = R. В прямоугольном треугольнике
, расположенной в плоскости а. Докажем, что точка М — общая точка плоскости а и сферы S(0, R). Для этого достаточно доказать, что ОМ = R. В прямоугольном треугольнике 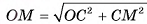
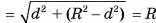 . Таким образом, мы доказали, что пересечение плоскости а и сферы S(0, R) есть окружность с центром в точке С и радиусом
. Таким образом, мы доказали, что пересечение плоскости а и сферы S(0, R) есть окружность с центром в точке С и радиусом 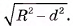
Теорема доказана.
Заметим, что утверждение теоремы остается верным и в случае, если плоскость а проходит через центр сферы. Убедитесь в этом самостоятельно.
Из доказанной теоремы следует, что сечение шара плоскостью есть круг, а основание перпендикуляра, проведенного из центра шара к плоскости сечения, есть центр круга, полученного в сечении.
Плоскость, проходящая через центр сферы (шара), называется диаметральной плоскостью.
Сечение сферы (шара) диаметральной плоскостью называется большой окружностью (большим кругом).
Нетрудно понять, что плоскость а и сфера (шар) радиусом R имеют общие точки, если выполняется неравенство 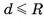 (d — расстояние от центра шара до плоскости а).
(d — расстояние от центра шара до плоскости а).
Определение. Касательной плоскостью к сфере называется плоскость, имеющая со сферой только одну общую точку, а их общая точка называется точкой касания плоскости и сферы.
Касательной плоскостью к шару называется касательная плоскость к сфере, которая является границей этого шара.
Прямая, лежащая в касательной плоскости сферы (шара) и проходящая через точку касания, называется касательной к сфере (шару). По определению касательная плоскость имеет со сферой только одну общую точку, следовательно, касательная прямая также имеет со сферой только одну общую точку — точку касания.
Следующая теорема показывает, что касательная плоскость к сфере существует.
Теорема 2 (признак касательной плоскости к сфере).
Плоскость, перпендикулярная радиусу сферы и проходящая через его конец, лежащий на сфере, касается сферы.
Дано:
OF — радиус сферы, S(0, R),
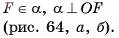
Доказать: а касается сферы в точке F.
Доказательство:
Пусть М — произвольная точка плоскости а, отличная от точки F. По условию 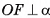 , следовательно, ОМ — наклонная к плоскости а, и поэтому ОМ > OF, т. е. ОМ > R. Отсюда следует, что точка М не лежит на сфере, значит, плоскость а имеет только одну общую точку F со сферой, т. е. касается сферы в точке F.
, следовательно, ОМ — наклонная к плоскости а, и поэтому ОМ > OF, т. е. ОМ > R. Отсюда следует, что точка М не лежит на сфере, значит, плоскость а имеет только одну общую точку F со сферой, т. е. касается сферы в точке F.
Теорема доказана.
Теорема 3 (о свойстве касательной плоскости к сфере).
Касательная плоскость к сфере перпендикулярна радиусу, проведенному в точку касания.
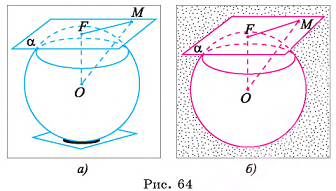
Доказательство:
Пусть плоскость а касается сферы S(0, R) в точке F (рис. 64, о, б). Докажем, что 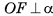 . По определению касательной плоскости к сфере точка F является единственной общей точкой плоскости а и сферы S(0, R). Следовательно, любая другая точка М плоскости а лежит вне сферы, и поэтому
. По определению касательной плоскости к сфере точка F является единственной общей точкой плоскости а и сферы S(0, R). Следовательно, любая другая точка М плоскости а лежит вне сферы, и поэтому 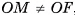 , т. е. либо ОМ < OF, либо ОМ > OF. Заметим, что неравенство ОМ < OF не может выполняться. Действительно, если ОМ < OF, то на прямой FM найдется точка X, отличная от точки F, для которой СХ = OF. Так как
, т. е. либо ОМ < OF, либо ОМ > OF. Заметим, что неравенство ОМ < OF не может выполняться. Действительно, если ОМ < OF, то на прямой FM найдется точка X, отличная от точки F, для которой СХ = OF. Так как 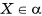 , то сфера и плоскость а имеют две общие точки, а это противоречит определению касательной плоскости к сфере. Таким образом, ОМ > OF. Следовательно, длина отрезка OF — расстояние от центра О сферы до плоскости, т. е.
, то сфера и плоскость а имеют две общие точки, а это противоречит определению касательной плоскости к сфере. Таким образом, ОМ > OF. Следовательно, длина отрезка OF — расстояние от центра О сферы до плоскости, т. е. 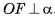 . Значит, длина отрезка OF — кратчайшее расстояние среди расстояний от центра О до точек плоскости а, т. е.
. Значит, длина отрезка OF — кратчайшее расстояние среди расстояний от центра О до точек плоскости а, т. е. 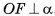 .
.
Теорема доказана.
Многогранники и сфера
Рассмотрим понятия многогранника, вписанного в сферу, и многогранника, описанного около сферы.
Многогранник (например, пирамида или призма) называется вписанным в сферу, если все его вершины лежат на сфере. При этом сфера называется описанной около многогранника (пирамиды, призмы).
Многогранник называется вписанным в шар, если все его вершины лежат на границе этого шара. При этом шар называется описанным, около многогранника.
Центр О сферы S(0, R), описанной около многогранника, находится на расстоянии, равном радиусу R сферы, от каждой вершины многогранника.
На рисунке 65 а, б изображена треугольная пирамида FABC, вписанная в сферу S(0, R). Вершины основания ABC пирамиды лежат на окружности, по которой плоскость основания пересекает сферу (OF = OA - OB = ОС - R).
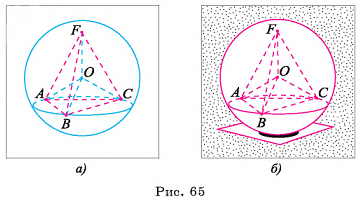
Многогранник называется описанным около сферы (шара), если сфера (шар) касается всех граней многогранника. При этом сфера и шар называются вписанными в многогранник.
Центр О сферы S(0, г), вписанной в многогранник, находится на расстоянии, равном радиусу г сферы, от каждой из плоскостей, содержащих грани многогранника.
Пример №14
Докажите, что около любой правильной пирамиды можно описать сферу.
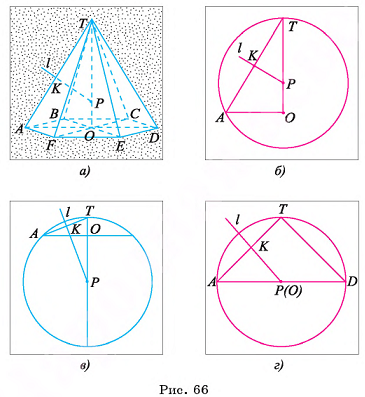
Доказательство:
1) Рассмотрим для определенности правильную шестиугольную пирамиду TABCDEF (рис. 66, а). Пусть ТО — высота этой пирамиды. В плоскости AT О проведем серединный перпендикуляр I к отрезку AT 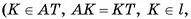
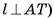 . Обозначим буквой Р точку пересечения прямых I и ТО. Тогда РТ = РА (любая точка серединного перпендикуляра к отрезку AT равноудалена от концов этого отрезка).
. Обозначим буквой Р точку пересечения прямых I и ТО. Тогда РТ = РА (любая точка серединного перпендикуляра к отрезку AT равноудалена от концов этого отрезка).
2)Точка Р равноудалена от вершин основания правильной пирамиды, т. е. PA = PB = PC = PD = PE = PF (так как 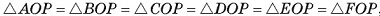 , эти треугольники прямоугольные, ОР — их общий катет, OA = OB = ОС = OD = ОЕ = OF).
, эти треугольники прямоугольные, ОР — их общий катет, OA = OB = ОС = OD = ОЕ = OF).
3)Таким образом, РТ = РА = РВ = PC = PD = РЕ = PF, т. е. точка Р равноудалена от всех вершин пирамиды. Сфера с центром в точке Р и радиусом РТ есть сфера, описанная около рассматриваемой правильной пирамиды. Таким образом, центр Р сферы, описанной около правильной пирамиды, есть точка пересечения прямой, на которой лежит высота пирамиды, и серединного перпендикуляра к боковому ребру, проведенного в плоскости, содержащей высоту и боковое ребро пирамиды.
Центр сферы может лежать на высоте пирамиды (рис. 66, б), лежать на продолжении высоты (рис. 66, в) или совпадать с основанием высоты пирамиды (рис. 66, г).
Пример №15
Докажите, что если в основание пирамиды можно вписать окружность, а основание высоты пирамиды является центром этой окружности, то в пирамиду можно вписать сферу.
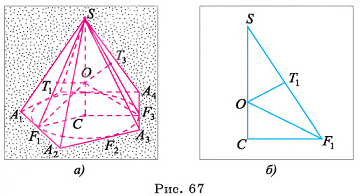
Доказательство:
Рассмотрим для определенности пятиугольную пирамиду 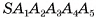 Пусть
Пусть 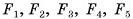 — точки касания вписанной в основание пирамиды окружности со сторонами основания, С — центр вписанной окружности (рис. 67, а, б). Прямоугольные треугольники
— точки касания вписанной в основание пирамиды окружности со сторонами основания, С — центр вписанной окружности (рис. 67, а, б). Прямоугольные треугольники 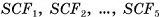 равны и SC — их общий катет. Значит, биссектрисы углов при вершинах
равны и SC — их общий катет. Значит, биссектрисы углов при вершинах 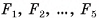 пересекают этот катет в одной и той же точке О. Пусть
пересекают этот катет в одной и той же точке О. Пусть 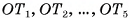 — перпендикуляры, опущенные на гипотенузы
— перпендикуляры, опущенные на гипотенузы 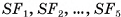 соответственно. Плоскость
соответственно. Плоскость 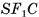 перпендикулярна плоскости
перпендикулярна плоскости 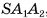 , следовательно,
, следовательно, 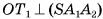 . Аналогично
. Аналогично 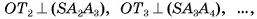
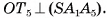 Так как
Так как 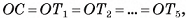 то точка О находится на одном и том же расстоянии от плоскостей всех граней пирамиды. Значит, сфера с центром О и радиусом г = ОС касается всех граней, т. е. вписана в данную пирамиду.
то точка О находится на одном и том же расстоянии от плоскостей всех граней пирамиды. Значит, сфера с центром О и радиусом г = ОС касается всех граней, т. е. вписана в данную пирамиду.
Пример №16
Сфера радиусом 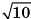 см касается всех сторон прямоугольного треугольника ABD
см касается всех сторон прямоугольного треугольника ABD 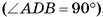 , длины сторон которого 3 см, 4 см, 5 см. Вычислите расстояние от центра сферы до плоскости треугольника.
, длины сторон которого 3 см, 4 см, 5 см. Вычислите расстояние от центра сферы до плоскости треугольника.
Решение:
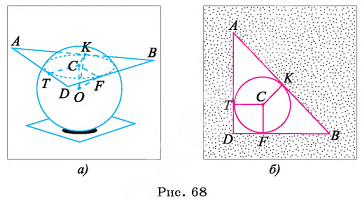
1)Пусть Т, К, F — точки касания сферы со сторонами треугольника, точка С — основание перпендикуляра, проведенного из центра О сферы к плоскости треугольника (точка С совпадает с центром окружности, полученной в сечении) (рис. G8, а).
2)Отрезки ОТ, OK, OF перпендикулярны сторонам треугольника (радиус, проведенный в точку касания). Отрезок ОС перпендикулярен плоскости треугольника, значит, он тоже перпендикулярен сторонам треугольника. Отсюда следует, что отрезки СТ, СК, CF перпендикулярны сторонам треугольника.
3)Из равенства прямоугольных треугольников ОСТ, ОСК, OFC (ОТ = О К = OF, ОС — общая сторона) следует, что СТ = СК = CF, т. е. точка С — центр окружности, вписанной в треугольник ADB. Радиус этой окружности г=р-с 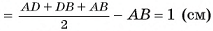 (рис. 68, б).
(рис. 68, б).
4)В прямоугольном треугольнике ОСК 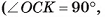
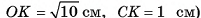 длина катета
длина катета 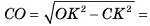
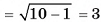 (см). Ответ: 3 см.
(см). Ответ: 3 см.
Цилиндр
В этом параграфе мы изучим свойства геометрического тела, называемого цилиндром. В окружающей нас природе существует множество объектов, являющихся физическими моделями указанной фигуры. Например, форму цилиндра имеют многие детали машин и элементы многих архитектурных сооружений (рис. 71, а).
В некоторой плоскости а рассмотрим окружность 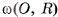 с центром О и радиусом R. Через каждую точку окружности
с центром О и радиусом R. Через каждую точку окружности 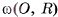 проведем прямую, перпендикулярную плоскости а.
проведем прямую, перпендикулярную плоскости а.
Цилиндрической поверхностью называется фигура, образованная этими прямыми, а сами прямые называются образующими цилиндрической поверхности.
Все образующие цилиндрической поверхности параллельны друг другу, так как они перпендикулярны плоскости а.
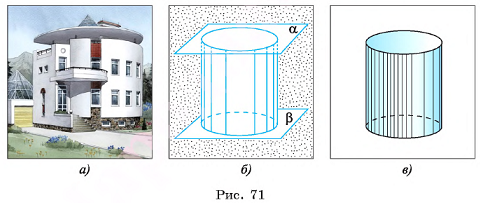
Прямым круговым цилиндром или просто цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями а и р, которые перпендикулярны образующим цилиндрической поверхности (рис. 71, б, в).
Боковой поверхностью цилиндра называется часть цилиндрической поверхности, расположенная между секущими плоскостями 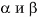 , которые перпендикулярны ее образующим (рис. 72, а), а части (круги), отсекаемые цилиндрической поверхностью на параллельных плоскостях аир, называются основаниями цилиндра (рис. 72, б).
, которые перпендикулярны ее образующим (рис. 72, а), а части (круги), отсекаемые цилиндрической поверхностью на параллельных плоскостях аир, называются основаниями цилиндра (рис. 72, б).
Образующей цилиндра называется отрезок (или длина этого отрезка) образующей цилиндрической поверхности, расположенный между параллельными плоскостями, в которых лежат основания цилиндра. Все образующие цилиндра параллельны и равны между собой.
Осью цилиндра называется отрезок 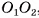 , соединяющий центры кругов, являющихся основаниями цилиндра (см. рис. 72, а, б).
, соединяющий центры кругов, являющихся основаниями цилиндра (см. рис. 72, а, б).
Высотой цилиндра называется перпендикуляр (или длина этого перпендикуляра), проведенный из какой-нибудь точки плоскости одного основания цилиндра к плоскости другого основания.
Радиусом цилиндра называется радиус его основания.
Цилиндр называется равносторонним, если его высота равна диаметру основания.
Если цилиндр с основанием радиусом R спроектировать на плоскость основания параллельно какой-либо его образующей, то проекцией цилиндра будет круг радиусом R (рис. 72, в).
Цилиндр можно получить поворотом, прямоугольника, вокруг одной из его сторон на 360°. На рисунке 73, а изображен цилиндр, полученный поворотом прямоугольника ABCD вокруг стороны АВ. В этом случае боковая поверхность цилиндра образуется поворотом стороны CD, а основания — поворотом сторон ВС и AD.
Если секущая плоскость параллельна оси ОхОг цилиндра, то сечением цилиндра служит прямоугольник, две стороны
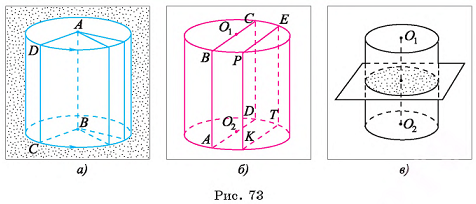
которого — образующие, а две другие — хорды оснований цилиндра. Примером такого сечения служит прямоугольник КТЕР, изображенный на рисунке 73, б.
Осевым, сечением, цилиндра называется сечение цилиндра плоскостью, проходящей через его ось.
Осевое сечение цилиндра — прямоугольник, две стороны которого есть образующие цилиндра, а две другие — диаметры его оснований. На рисунке 73, б изображено осевое сечение AJBCD.
Секущая плоскость, перпендикулярная оси цилиндра, пересекает его по кругу (рис. 73, в).
Призма называется вписанной в цилиндр, если ее основания вписаны в основания цилиндра, и призма, описана около цилиндра, если ее основания описаны около оснований цилиндра.
Например, на рисунке 74, а изображена треугольная призма 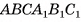 , вписанная в цилиндр, а на рисунке 74, б, в — треугольная призма
, вписанная в цилиндр, а на рисунке 74, б, в — треугольная призма 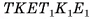 , описанная около цилиндра.
, описанная около цилиндра.
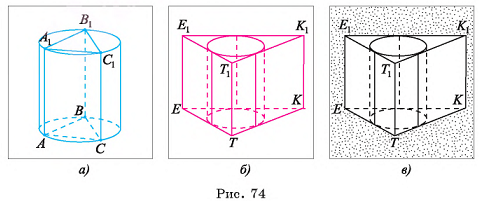
Высота призмы, вписанной в цилиндр или описанной около него, равна высоте цилиндра.
Цилиндр и сфера
Сфера называется вписанной в цилиндр, если она касается оснований цилиндра и каждой его образующей. При этом цилиндр называется описанным, около сферы (рис. 75, а).
Шар называется вписанным в цилиндр, если он касается оснований цилиндра и каждой его образующей. При этом цилиндр называется описанным около шара.
Цилиндр называется вписанным в сферу, если окружности оснований цилиндра являются сечениями сферы. При этом сфера называется описанной около цилиндра (рис. 75, б).
Цилиндр называется вписанным, в шар, если основания цилиндра являются сечениями шара. При этом шар называется описанным около цилиндра.
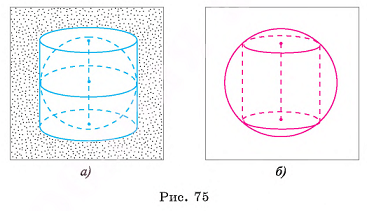
Площадь боковой и полной поверхностей цилиндра
Теперь рассмотрим вопрос о вычислении площади боковой и полной поверхностей цилиндра.
Пусть в цилиндр вписана правильная n-угольная призма. Если число п сторон основания правильной n-угольной призмы, вписанной в цилиндр, неограниченно возрастает, тогда призма все меньше и меньше отличается от цилиндра. Можно доказать, что существует число, к которому стремится площадь боковой поверхности такой призмы при неограниченном возрастании числа сторон ее оснований. За площадь боковой поверхности цилиндра принимается число, к которому стремится площадь боковой поверхности правилmной призмы, вписанной в цилиндр, когда число сторон оснований этой призмы неограниченно возрастает.
Теорема 1 (о площади боковой поверхности цилиндра).
Площадь боковой поверхности цилиндра равна произведению длины окружности его основания на высоту (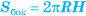 , где R — радиус основания цилиндра, Н — его высота).
, где R — радиус основания цилиндра, Н — его высота).
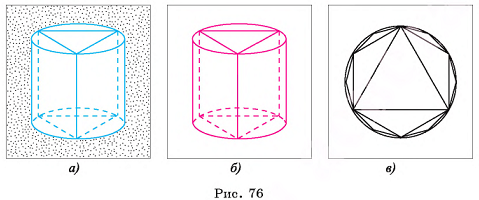
Доказательство:
Пусть Р„ и Н соответственно периметр основания и высота правильной «-угольной призмы, вписанной в цилиндр (рис. 76, а, б). Тогда площадь боковой поверхности этой призмы  . Предположим, что число сторон правильного многоугольника, вписанного в основание цилиндра, неограниченно растет (рис. 76, в). Тогда периметр Рn стремится к длине окружности
. Предположим, что число сторон правильного многоугольника, вписанного в основание цилиндра, неограниченно растет (рис. 76, в). Тогда периметр Рn стремится к длине окружности 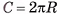 , где R — радиус основания цилиндра, а высота Н не изменяется. Таким образом, площадь боковой поверхности призмы стремится к числу
, где R — радиус основания цилиндра, а высота Н не изменяется. Таким образом, площадь боковой поверхности призмы стремится к числу 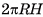 , т. е. площадь боковой поверхности цилиндра равна
, т. е. площадь боковой поверхности цилиндра равна 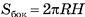 .
.
Теорема доказана.
Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. Площадь каждого основания цилиндра равна 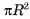 , следовательно, площадь полной поверхности цилиндра
, следовательно, площадь полной поверхности цилиндра 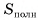 вычисляется по формуле
вычисляется по формуле 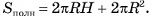
Если боковую поверхность цилиндра «разрезать» по образующей FT (рис. 77, а) и развернуть так, чтобы все образующие оказались в одной плоскости, то в результате мы получим прямоугольник 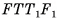 который называется разверткой
который называется разверткой
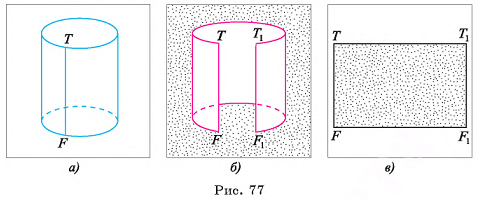
боковой поверхности цилиндра. Сторона 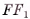 прямоугольника есть развертка окружности основания цилиндра, следовательно,
прямоугольника есть развертка окружности основания цилиндра, следовательно, 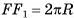 , а его сторона FT равна образующей цилиндра, т. е. FT = H (рис. 77, б, в). Таким образом, площадь
, а его сторона FT равна образующей цилиндра, т. е. FT = H (рис. 77, б, в). Таким образом, площадь 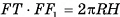 развертки боковой поверхности цилиндра равна площади его боковой поверхности.
развертки боковой поверхности цилиндра равна площади его боковой поверхности.
Объем цилиндра
Теперь рассмотрим вопрос о вычислении объема цилиндра.
За объем цилиндра принимается число, к которому стремится объем правильной призмы, вписанной в цилиндр, когда число сторон ее оснований неограниченно возрастает.
Теорема 2 (об объеме цилиндра).
Объем цилиндра равен произведению площади основания на высоту ( , где R, Н — радиус и высота цилиндра соответственно).
, где R, Н — радиус и высота цилиндра соответственно).
Доказательство:
Пусть S„ — площадь основания, Н — высота правильной п-угольной призмы, вписанной в цилиндр. Тогда объем этой призмы Vn = S„H. Предположим, что число сторон основания вписанной в цилиндр призмы неограниченно возрастает. Тогда S„ будет стремиться к площади 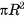 основания цилиндра, а высота Н остается неизменной. Таким образом, объем SnH призмы будет стремиться к числу
основания цилиндра, а высота Н остается неизменной. Таким образом, объем SnH призмы будет стремиться к числу 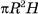 , т. е. объем цилиндра равен V=
, т. е. объем цилиндра равен V=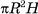 .
.
Теорема доказана.
Пример №17
В равносторонний цилиндр радиусом 2 см вписана правильная треугольная призма 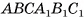 . Вычислите объем пирамиды OACF, где точка О — центр грани
. Вычислите объем пирамиды OACF, где точка О — центр грани  , а точка F — середина ребра АВ.
, а точка F — середина ребра АВ.

Решение:
1)Объем пирамиды вычислим по формуле 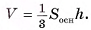 Так как
Так как 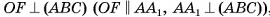 , то
, то 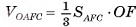 (рис. 78, а, б).
(рис. 78, а, б).
2)Пусть х — длина стороны основания, тогда площадь основания 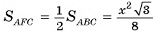 (рис. 78, в)
(рис. 78, в)
3)В треугольнике 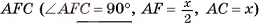 длина катета
длина катета 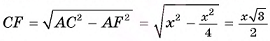 . Так как треугольник АСВ равносторонний, то
. Так как треугольник АСВ равносторонний, то 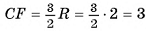 (см). Из уравнения
(см). Из уравнения 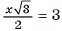 найдем, что
найдем, что 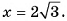
4)Таким образом, 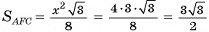 (см2), а
(см2), а 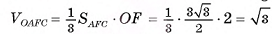 (см3).
(см3).
Ответ: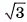 см3.
см3.
Пример №18
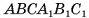 — прямая призма, основание которой есть прямоугольный треугольник
— прямая призма, основание которой есть прямоугольный треугольник 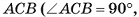
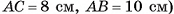 . Вычислите объем цилиндра, вписанного в призму, если объем пирамиды
. Вычислите объем цилиндра, вписанного в призму, если объем пирамиды  равен 16 см3.
равен 16 см3.
Решение:
1) Объем цилиндра вычислим по формуле 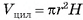 . Заметим, что высота цилиндра равна длине ребра
. Заметим, что высота цилиндра равна длине ребра 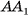 призмы, а радиус г равен радиусу окружности, вписанной в прямоугольный треугольник ABC (рис. 79, а, б, в).
призмы, а радиус г равен радиусу окружности, вписанной в прямоугольный треугольник ABC (рис. 79, а, б, в).
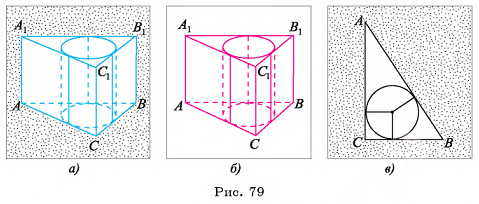
2)В треугольнике 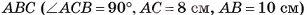 длина катета
длина катета 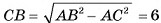 см.
см.
3)Объем пирамиды 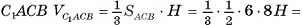 8Н. По условию 8Н = 16, следовательно, Н = 2 см.
8Н. По условию 8Н = 16, следовательно, Н = 2 см.
4)Радиус вычислим по формуле 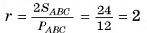 (см).
(см).
Таким образом, 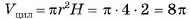 (см3).
(см3).
Ответ: 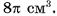
Конус
Пусть окружность 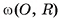 лежит в некоторой плоскости
лежит в некоторой плоскости 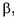 , а прямая
, а прямая 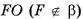 перпендикулярна этой плоскости. Через точку F и каждую точку окружности
перпендикулярна этой плоскости. Через точку F и каждую точку окружности 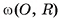 проведем прямую. Конической поверхностью называется фигура, образованная этими прямыми, а сами прямые называются образующими, конической поверхности, точка F называется ее вершиной, а прямая FO — осью конической поверхности (рис. 83, а).
проведем прямую. Конической поверхностью называется фигура, образованная этими прямыми, а сами прямые называются образующими, конической поверхности, точка F называется ее вершиной, а прямая FO — осью конической поверхности (рис. 83, а).
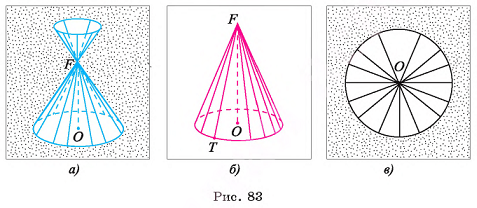
Конусом называется геометрическое тело, ограниченное конической поверхностью и кругом с границей 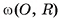 (рис. 83, б).
(рис. 83, б).
Основанием конуса называется круг, границей которого служит окружность 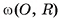 . Вершиной конуса называется вершина S конической поверхности.
. Вершиной конуса называется вершина S конической поверхности.
Образующей конуса называется отрезок (или длина этого отрезка) образующей конической поверхности, расположенный между его вершиной и основанием. Например, отрезок 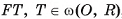 , — образующая конуса (см. рис. 83, б). Все образующие конуса равны между собой.
, — образующая конуса (см. рис. 83, б). Все образующие конуса равны между собой.
Боковой поверхностью конуса называется фигура, образованная всеми образующими конуса.
Высотой конуса называется отрезок FO (или его длина), где точка F — вершина конуса, а точка О — центр его основания, прямая FO называется осью конуса.
Если конус с вершиной F спроектировать на плоскость основания параллельно его оси FO, то проекцией конуса будет круг с центром О и радиусом R, а радиусы этого круга являются проекциями образующих конуса (рис. 83, в).
Конус может быть получен поворотом прямоугольного треугольника вокруг одного из катетов на 360°. На рисунке 84, а изображен конус, полученный поворотом прямоугольного треугольника SOC вокруг катета SO. В этом случае боковая поверхность конуса образуется поворотом гипотенузы SC, а круг, являющийся основанием конуса, — поворотом катета ОС.
Если плоскость проходит через высоту SO конуса, то сечение конуса этой плоскостью называется осевым и представляет собой равнобедренный треугольник, основанием которого является диаметр основания конуса, а боковыми сторонами — образующие конуса. Например, на рисунке 84, б изображено осевое сечение SAB.
Если плоскость проходит через внутреннюю точку высоты SO конуса и перпендикулярна ей, то сечением конуса является круг, центр которого есть точка пересечения высоты и этой плоскости (рис. 84, в).
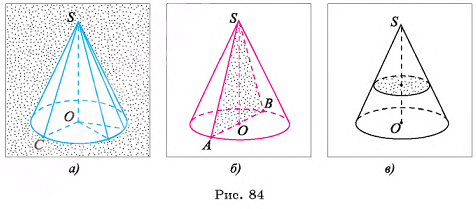
Усеченный конус
Пусть плоскость а проходит через внутреннюю точку О1 высоты SO конуса и перпендикулярна ей. Усеченным конусом называется геометрическое тело, ограниченное боковой поверхностью конуса, его основанием и секущей плоскостью а, перпендикулярной оси конуса (рис. 85, а).
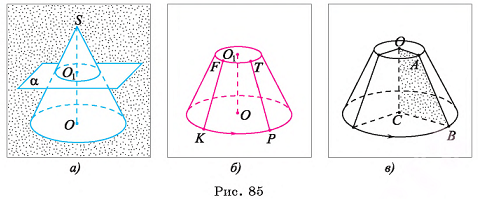
Основаниями усеченного конуса называются основание данного конуса и круг, полученный в сечении этого конуса плоскостью а.
Высотой усеченного конуса называется отрезок 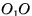 (или его длина), соединяющий центры его оснований, прямая
(или его длина), соединяющий центры его оснований, прямая 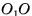 называется его осью (рис. 85, б).
называется его осью (рис. 85, б).
Часть боковой поверхности конуса, ограничивающая усеченный конус, называется его боковой поверхностью, а отрезки образующих конуса, расположенные между основаниями усеченного конуса, называются его образующими.
Все образующие усеченного конуса равны между собой.
На рисунке 85, б изображены образующие FK и TP усеченного конуса.
Усеченный конус может быть получен при повороте на 360° прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к основаниям.
На рисунке 85, в изображен усеченный конус, полученный поворотом прямоугольной трапеции АВСО вокруг стороны СО. При этом боковая поверхность образуется поворотом боковой стороны АВ, а основания усеченного конуса — поворотом оснований OA и СВ трапеции.
3. Конус и сфера. Конус называется вписанным в сферу, если его вершина принадлежит сфере, а окружность основания является сечением сферы. При этом сфера называется описанной около конуса (рис. 86, а, б).
Конус называется вписанным в шар, если вершина конуса принадлежит границе этого шара, а его основание является сечением шара. При этом шар называется описанным около конуса.
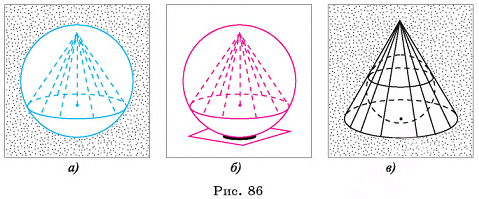
Сфера называется вписанной в конус, если сфера касается основания конуса и каждой его образующей. При этом конус называется описанным около сферы (рис. 86, в).
Шар называется вписанным в конус, если он касается основания конуса и каждой его образующей. При этом конус называется описанным около шара.
Конус и пирамида
Конус называется вписанным в пирамиду (пирамида — описанной около конуса), если основание конуса вписано в основание пирамиды, а вершины конуса и пирамиды совпадают. На рисунке 87, а, б изображен конус, вписанный в треугольную пирамиду SABC.
Пирамида называется вписанной в конус (конус — описанным около пирамиды), если ее основание вписано в основание конуса, а боковые ребра являются образующими конуса. Например, на рисунке 87, в изображена четырехугольная пирамида SABCD, вписанная в конус.
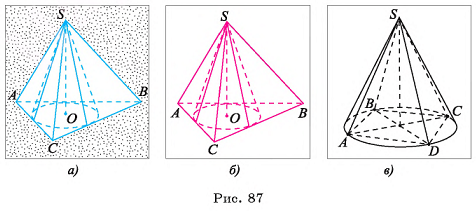
Площади боковой и полной поверхностей конуса
Рассмотрим вопрос о вычислении площади боковой и полной поверхности конуса и усеченного конуса.
Пусть в конус вписана правильная и-угольная пирамида. Если число n сторон основания правильной n-угольной пирамиды, вписанной в конус, неограниченно возрастает, то пирамида все меньше и меньше отличается от конуса. Можно доказать, что существует число, к которому при этом стремится площадь боковой поверхности пирамиды.
За площадь боковой поверхности конуса принимается число, к которому стремится площадь боковой поверхности, вписанной в этот конус правильной n-угольной пирамиды, когда число п сторон основания неограниченно возрастает.
Теорема 1 (о площади боковой поверхности конуса).
Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую (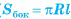 где R — радиус основания конуса, I — образующая).
где R — радиус основания конуса, I — образующая).
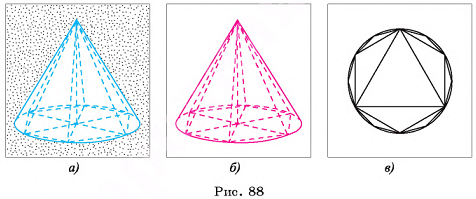
Доказательство:
Пусть 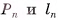 — соответственно периметр основания и длина апофемы правильной n-угольной пирамиды, вписанной в конус (рис. 88, а, б). Площадь боковой поверхности этой пирамиды вычисляется по формуле
— соответственно периметр основания и длина апофемы правильной n-угольной пирамиды, вписанной в конус (рис. 88, а, б). Площадь боковой поверхности этой пирамиды вычисляется по формуле 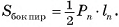
Предположим, что число сторон правильного многоугольника, вписанного в основание конуса, неограниченно возрастает (рис. 88, в). Тогда периметр 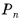 стремится к длине
стремится к длине 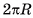 окружности основания, а длина
окружности основания, а длина 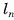 апофемы — к образующей I конуса.
апофемы — к образующей I конуса.
Таким образом, площадь боковой поверхности вписанной в конус пирамиды стремится к числу 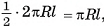 , т. е. площадь
, т. е. площадь 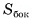 боковой поверхности конуса равна
боковой поверхности конуса равна 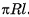 .
.
Теорема доказана.
Если боковую поверхность конуса развернуть на плоскость, «разрезав» ее по одной из образующих SB, то в результате мы получим круговой сектор 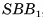 , который называется разверткой боковой поверхности конуса. Радиус полученного кругового сектора равен образующей конуса, а длина дуги сектора равна длине окружности основания конуса (рис. 89, а, б, в).
, который называется разверткой боковой поверхности конуса. Радиус полученного кругового сектора равен образующей конуса, а длина дуги сектора равна длине окружности основания конуса (рис. 89, а, б, в).
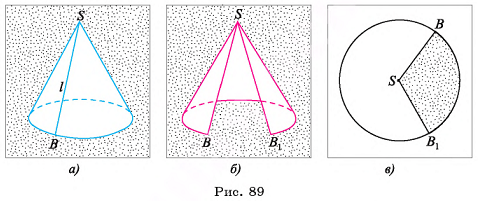
Площадь кругового сектора 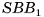 равна
равна 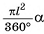 , где а — градусная мера дуги
, где а — градусная мера дуги 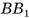 . Так как длина дуги
. Так как длина дуги 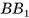 равна
равна 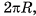 , то
, то 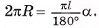 Отсюда
Отсюда 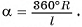 Следовательно, площадь сектора
Следовательно, площадь сектора 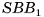 равна
равна 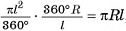 , т. е. площадь боковой поверхности конуса равна площади развертки его боковой поверхности.
, т. е. площадь боковой поверхности конуса равна площади развертки его боковой поверхности.
Площадью полной поверхности конуса называется сумма площади боковой поверхности и площади основания. Таким образом, площадь полной поверхности конуса вычисляется по формуле 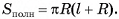
Пример №19
Докажите, что площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на длину образующей (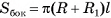 , где
, где 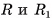 — радиусы оснований, I — образующая).
— радиусы оснований, I — образующая).
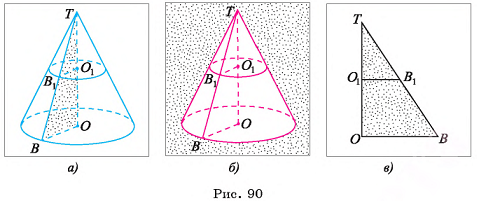
Доказательство:
1)Пусть точка Т — вершина конуса, из которого получен усеченный конус, 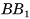 — одна из образующих усеченного конуса, а точки
— одна из образующих усеченного конуса, а точки 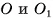 — центры его оснований, OB = R,
— центры его оснований, OB = R, 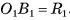 . Тогда площадь боковой поверхности усеченного конуса равна разности боковых поверхностей двух конусов, т. е.
. Тогда площадь боковой поверхности усеченного конуса равна разности боковых поверхностей двух конусов, т. е. 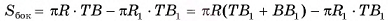 (рис. 90, а, б).
(рис. 90, а, б).
2)Так как 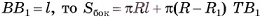 . Из подобия прямоугольных треугольников
. Из подобия прямоугольных треугольников  (рис. 90, а, б, в) следует, что
(рис. 90, а, б, в) следует, что 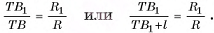 Отсюда найдем
Отсюда найдем 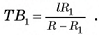
Таким образом,
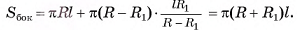
Площадью полной поверхности усеченного конуса называется сумма площадей его боковой поверхности и оснований. Следовательно, площадь полной поверхности усеченного конуса вычисляется по формуле 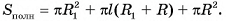
Объем конуса
Рассмотрим вопрос о вычислении объема конуса.
За объем, конуса принимается число, к которому стремится объем правильной пирамиды, вписанной в конус, когда число сторон основания пирамиды неограниченно возрастает.
Теорема 2 (об объеме конуса).
Объем конуса равен одной трети произведения площади основания на высоту
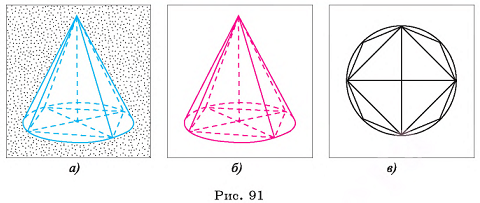
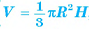 , где R — радиус основания конуса, Н — его высота).
, где R — радиус основания конуса, Н — его высота).
Доказательство:
Пусть S„ — площадь основания, Н — высота правильной /1-угольной пирамиды, вписанной в конус (рис. 91, а, б).
Тогда объем этой пирамиды 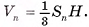 Предположим, что число сторон основания вписанной в конус пирамиды неограниченно возрастает (рис. 91, в). Тогда площадь Sn основания пирамиды будет стремиться к площади
Предположим, что число сторон основания вписанной в конус пирамиды неограниченно возрастает (рис. 91, в). Тогда площадь Sn основания пирамиды будет стремиться к площади 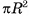 основания конуса, а высота Н остается неизменной. Таким образом, объем
основания конуса, а высота Н остается неизменной. Таким образом, объем 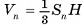 пирамиды будет стремиться к числу
пирамиды будет стремиться к числу 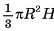 , т. е. объем конуса
, т. е. объем конуса 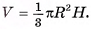
Теорема доказана.
Площадь сферы
Рассмотрим вопрос о нахождении площади сферы и ее частей. Для нахождения площади сферы можно воспользоваться следующей теоремой.
Теорема 1 (о площади сферы).
Площадь сферы равна 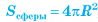 , где R — радиус сферы.
, где R — радиус сферы.
Прежде чем доказать эту теорему, рассмотрим вопрос о нахождении площадей частей сферы, на которые разбивает сферу секущая плоскость.
За площадь части сферы, образованной при повороте какой-нибудь дуги (АЕ) полуокружности вокруг диаметра АВ на 360°, принимается число, к которому стремится площадь поверхности, образуемой при повороте на 360° вокруг того же диаметра правильной вписанной ломаной ACDE, когда ее звенья неограниченно уменьшаются (рис. 96, а).
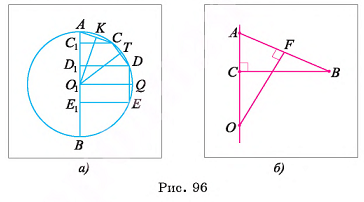
Докажем следующую вспомогательную теорему.
Теорема 2. Площадь боковой поверхности конуса, усеченного конуса и цилиндра равна произведению высоты соответствующего тела на длину окружности, радиус которой есть перпендикуляр, проведенный из середины образующей до пересечения с осью тела.
Доказательство:
1) Проведем доказательство для конуса. Пусть конус образован при повороте треугольника АСВ вокруг катета АС, точка F — середина гипотенузы, 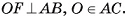 . Докажем, что площадь боковой поверхности конуса
. Докажем, что площадь боковой поверхности конуса 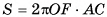 (рис. 96, б).
(рис. 96, б).
2)Площадь боковой поверхности конуса равна: 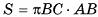 . Так как треугольник AFO подобен треугольнику АСВ (прямоугольные и имеют общий угол), то
. Так как треугольник AFO подобен треугольнику АСВ (прямоугольные и имеют общий угол), то 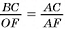 отсюда
отсюда 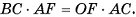
3)Теперь получим, что боковая поверхность конуса 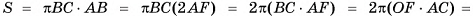
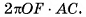
Что и требовалось доказать.
Доказательство для усеченного конуса и цилиндра проведите самостоятельно.
Теорема доказана.
Теорема 3. Пусть секущая плоскость перпендикулярна диаметру сферы радиусом R. Тогда площадь каждой из частей, на которые сфера разбивается секущей плоскостью, равна произведению длины большой окружности данной сферы на длину Н соответствующего отрезка диаметра: 
Доказательство:
1)Пусть часть сферы образована поворотом дуги АЕ вокруг диаметра АВ полуокружности, центр которой — точка  , а радиус — R. Впишем в эту дугу правильную ломаную линию ACDE (см. рис. 96, а). Поверхность, полученная при повороте этой ломаной, состоит из частей, образуемых при повороте ее звеньев AC, CD, DE, ... и т. д. Эти части представляют собой боковые поверхности конуса (образующая АС), усеченного конуса (образующая CD), цилиндра (образующая DE, если DE || АВ).
, а радиус — R. Впишем в эту дугу правильную ломаную линию ACDE (см. рис. 96, а). Поверхность, полученная при повороте этой ломаной, состоит из частей, образуемых при повороте ее звеньев AC, CD, DE, ... и т. д. Эти части представляют собой боковые поверхности конуса (образующая АС), усеченного конуса (образующая CD), цилиндра (образующая DE, если DE || АВ).
2)Заметим, что площадь каждой из указанных боковых поверхностей в силу теоремы 2 равна произведению высоты соответствующего тела (конуса, усеченного конуса, цилиндра) на длину окружности, радиус которой есть отрезок, соединяющий центр  полуокружности и середину соответствующего звена ломаной. Например, площадь боковой поверхности конуса, образованной поворотом звена АС, равна
полуокружности и середину соответствующего звена ломаной. Например, площадь боковой поверхности конуса, образованной поворотом звена АС, равна 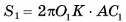 , где точка К — середина отрезка АС,
, где точка К — середина отрезка АС, 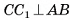 .
.
3)Для усеченного конуса, образующая которого CD, площадь боковой поверхности 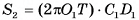 , где точка Т — середина отрезка
, где точка Т — середина отрезка 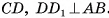 .
.
4)Для цилиндра, образующая которого DE, площадь боковой поверхности 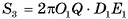 , где точка Q — середина отрезка
, где точка Q — середина отрезка 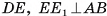 . Заметим, что отрезки, соединяющие центр
. Заметим, что отрезки, соединяющие центр 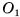 полуокружности и середины звеньев вписанной ломаной, равны между собой. Обозначим длину этих отрезков через а. Тогда площадь S поверхности, образованной при повороте ломаной
полуокружности и середины звеньев вписанной ломаной, равны между собой. Обозначим длину этих отрезков через а. Тогда площадь S поверхности, образованной при повороте ломаной 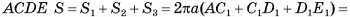
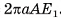 . При неограниченном увеличении числа звеньев вписанной ломаной длина а стремится к радиусу R сферы, а отрезок
. При неограниченном увеличении числа звеньев вписанной ломаной длина а стремится к радиусу R сферы, а отрезок 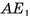 остается без изменения.
остается без изменения.
5)Следовательно, площадь S поверхности, образованной ломаной ACDE, стремится к 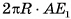 . Это число принимается за площадь соответствующей части сферы. Так как отрезок АЕ1 равен Н, то площадь этой части сферы
. Это число принимается за площадь соответствующей части сферы. Так как отрезок АЕ1 равен Н, то площадь этой части сферы 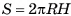 .
.
Теорема доказана.
Теперь воспользуемся результатом этой теоремы для доказательства теоремы 1 о площади сферы.
Разделим сферу на две части некоторой секущей плоскостью, перпендикулярной диаметру АБ. Пусть и 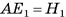 (рис. 97, а). Площадь сферы равна сумме площадей этих частей:
(рис. 97, а). Площадь сферы равна сумме площадей этих частей: 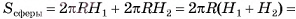
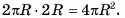
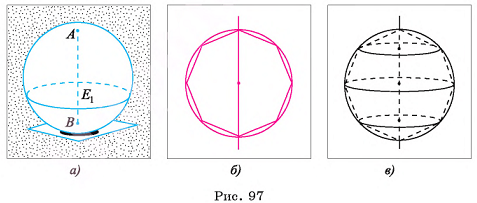
Объем шара
Рассмотрим вопрос о вычислении объема шара.
За объем шара принимается число, к которому стремится объем тела, полученного при повороте на 360° правильного многоугольника, вписанного в круг, при повороте которого на 360° получен данный шар, когда число сторон многоугольника неограниченно возрастает (рис. 97, б, в).
Для нахождения объема шара можно воспользоваться следующей теоремой, которую примем без доказательства.
Теорема 5 (об объеме шара).
Объем шара радиусом R вычисляется по формуле 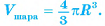
Объемы геометрических тел
В данной главе мы рассмотрели вопрос о вычислении объемов тел вращения, которые представляют собой частный случай геометрических тел. При этом объем для каждого из тел вращения рассматривался как число, к которому стремится объем вписанного в это тело правильного многогранника. Этим мы воспользовались для нахождения формул объемов цилиндра, конуса и шара.
Заметим, что понятие объема в общем случае для геометрических тел, в том числе и для тел вращения, можно определять аналогично понятию объема для многогранников.
Объем — это положительная величина, определенная для каждого из геометрических тел, числовое значение которой имеет следующие свойства:
- равные геометрические тела имеют равные объемы,',
- если геометрическое тело есть объединение конечного числа геометрических тел, каждые два из которых не имеют общих внутренних точек, то его объем равен сумме объемов этих тел',
- объем куба, ребро которого равно единице измерения длины, равен единице.
Вопрос о существовании и единственности объема для геометрических тел требует доказательства, но в рамках школьного курса геометрии он не рассматривается. Заметим, что в силу существования и единственности функции объема для тел вращения ее значения для цилиндра, конуса и шара находятся по полученным ранее формулам.
Пример №20
Длина стороны основания правильной треугольной пирамиды равна 4 см, а бокового ребра — 6 см. Вычислите площадь сферы, описанной около данной пирамиды.
Решение:
1) Площадь сферы вычисляется по формуле
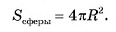
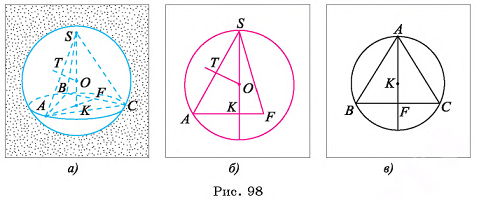
2)Центр О данной сферы есть точка пересечения прямой, содержащей высоту SK пирамиды и серединного перпендикуляра, проведенного в плоскости SAK к ребру (рис. 98, а, б).
3)Пусть точка Т — середина ребра SA. Треугольник STO подобен треугольнику SKA, следовательно, 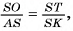
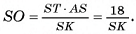
4)В треугольнике 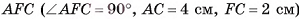
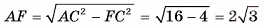 (см) (рис. 98, в).
(см) (рис. 98, в).
5)Из треугольника 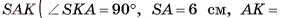
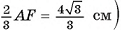 найдем длину катета
найдем длину катета 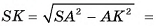
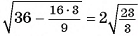 (см) (рис. 98, б).
(см) (рис. 98, б).
6) Таким образом, 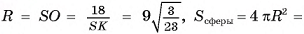
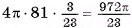 (см2).
(см2).
Пример №21
Длина образующей конуса равна 3 см. Вычислите объем шара, вписанного в конус, если образующая конуса наклонена к плоскости основания под углом ф.
Решение:
1)Объем шара вычисляется по формуле 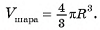
2)Центр вписанного в конус шара есть точка пересечения высоты SF конуса и биссектрисы угла SBA осевого сечения (рис. 99, а, б, в).
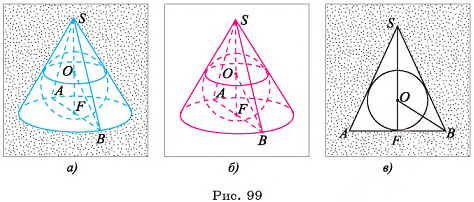
3)Из треугольника OFВ 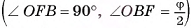 найдем
найдем 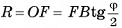 (см. рис. 99, а, б).
(см. рис. 99, а, б).
4)В треугольнике SFB 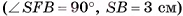 длина катета
длина катета 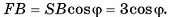
5)Таким образом,
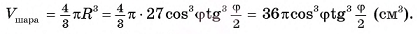
Ответ: 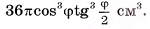
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |