
Сфера в геометрии - элементы, формулы, свойства с примерами
Сферой называется поверхность, полученная вращением окружности вокруг какого-либо ее диаметра (рис. 180). Центр этой окружности называется центром сферы.
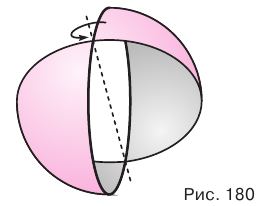
Отрезок, соединяющий центр сферы с любой ее точкой, называется радиусом сферы, отрезок, соединяющий две точки сферы, — хордой сферы, а хорда, которой принадлежит центр сферы, — диаметром сферы (рис. 181).
Из определения сферы следует, что все ее точки равноудалены от центра сферы. Поэтому все радиусы сферы равны друг другу.
Теоремы
Теорема 1.
Сечение сферы плоскостью есть окружность, центр которой совпадает с основанием перпендикуляра, опущенного из центра сферы на секущую плоскость.
Доказательство:
Пусть сфера с центром 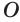
Пусть 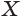 и
и 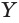 — произвольные точки линии пересечения сферы с плоскостью
— произвольные точки линии пересечения сферы с плоскостью 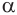 . Треугольники
. Треугольники 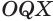 и
и 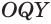 оба прямоугольные, так как отрезок
оба прямоугольные, так как отрезок 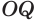 перпендикулярен плоскости
перпендикулярен плоскости 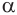 , а значит, и отрезкам
, а значит, и отрезкам 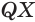 и
и 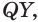 лежащим в этой плоскости.
лежащим в этой плоскости.
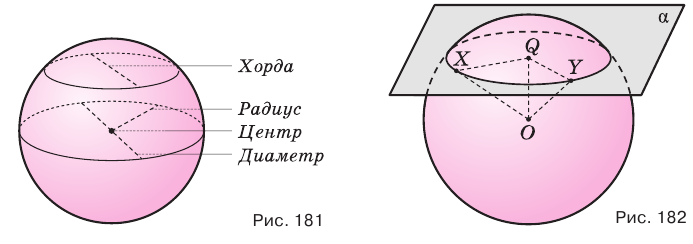
Отрезок 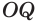 является общим катетом, а гипотенузы этих треугольников равны как радиусы сферы. Поэтому треугольники
является общим катетом, а гипотенузы этих треугольников равны как радиусы сферы. Поэтому треугольники 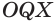 и
и 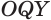 равны друг другу, а значит,
равны друг другу, а значит, 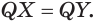 Получили, что любые две точки линии пересечения сферы плоскостью
Получили, что любые две точки линии пересечения сферы плоскостью 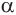 равноудалены от основания
равноудалены от основания  перпендикуляра, опущенного из центра сферы на эту плоскость. Значит, эта линия является окружностью с центром
перпендикуляра, опущенного из центра сферы на эту плоскость. Значит, эта линия является окружностью с центром  .
.
Следствие. Радиус 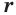 сечения сферы плоскостью удовлетворяет условию
сечения сферы плоскостью удовлетворяет условию 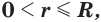 где
где 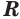 — радиус сферы.
— радиус сферы.
Сечение имеет наибольший радиус 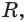 если секущая плоскость проходит через центр сферы, это сечение называют большой окружностью, а ограниченный ею круг — большим кругом.
если секущая плоскость проходит через центр сферы, это сечение называют большой окружностью, а ограниченный ею круг — большим кругом.
Плоскость, имеющая со сферой единственную общую точку, называется касательной плоскостью сферы. Общая точка сферы и касательной плоскости называется точкой касания.
Прямая касательной плоскости сферы, проходящая через точку касания, имеет со сферой единственную общую точку. Такая прямая называется касательной прямой сферы.
Теорема 2.
Касательная плоскость сферы перпендикулярна радиусу, проведенному в точку касания.
Доказательство:
Пусть плоскость 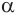 касается сферы с центром
касается сферы с центром 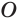 в точке
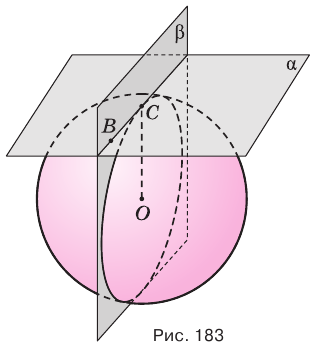
в точке  (рис. 183). Пусть
(рис. 183). Пусть 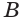 — произвольная точка плоскости
— произвольная точка плоскости 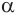 , отличная от точки
, отличная от точки  . Через точки
. Через точки 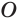 ,
,  ,
, 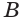 проведем плоскость
проведем плоскость 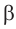 , она по теореме 1 пересекает сферу по окружности. По отношению к этой окружности прямая
, она по теореме 1 пересекает сферу по окружности. По отношению к этой окружности прямая 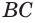 является касательной, так как точка
является касательной, так как точка  — их единственная общая точка. По свойству касательной к окружности радиус
— их единственная общая точка. По свойству касательной к окружности радиус 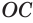 перпендикулярен прямой
перпендикулярен прямой 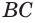 . Таким образом, радиус
. Таким образом, радиус 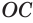 перпендикулярен любой прямой
перпендикулярен любой прямой 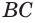 , проведенной в плоскости а через ее точку
, проведенной в плоскости а через ее точку  . Значит, радиус
. Значит, радиус 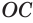 перпендикулярен плоскости
перпендикулярен плоскости 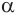 .
.
Теорема 3.
Если плоскость проходит через точку сферы и перпендикулярна радиусу, проведенному в эту точку, то она является касательной плоскостью сферы.
Доказательство:
Пусть плоскость  проходит через точку
проходит через точку  сферы и перпендикулярна радиусу
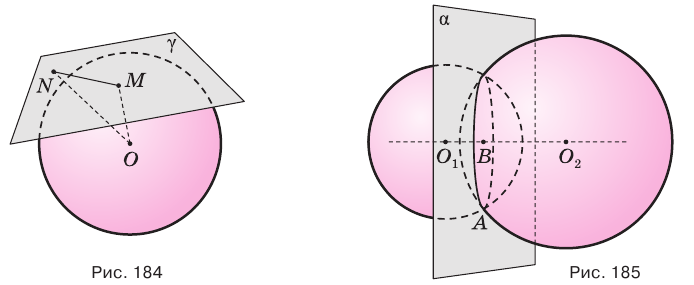
сферы и перпендикулярна радиусу 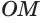 (рис. 184). Пусть
(рис. 184). Пусть 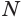 — произвольная точка плоскости
— произвольная точка плоскости  , отличная от точки
, отличная от точки  . Треугольник
. Треугольник 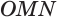 прямоугольный с гипотенузой
прямоугольный с гипотенузой 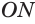 , и она длиннее катета. Поэтому точка
, и она длиннее катета. Поэтому точка 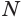 расположена вне сферы. Получается, что любая точка плоскости
расположена вне сферы. Получается, что любая точка плоскости  , кроме точки
, кроме точки  , не принадлежит сфере. Значит, точка
, не принадлежит сфере. Значит, точка  — единственная общая точка плоскости
— единственная общая точка плоскости  и сферы, а поэтому плоскость
и сферы, а поэтому плоскость  является касательной плоскостью сферы.
является касательной плоскостью сферы.
Теоремы 2 и 3 выражают соответственно свойство и признак касательной плоскости сферы.
Теорема 4.
Две сферы пересекаются по окружности, плоскость которой перпендикулярна прямой, проходящей через центры сфер.
Доказательство:
Пусть имеются две пересекающиеся сферы с центрами 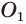 и
и 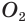 , и
, и 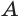 — какая-либо их общая точка (рис. 185). Через точку
— какая-либо их общая точка (рис. 185). Через точку 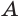 проведем плоскость
проведем плоскость 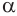 , перпендикулярную прямой
, перпендикулярную прямой 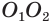 . Пусть эта плоскость пересекает прямую
. Пусть эта плоскость пересекает прямую 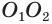 в точке
в точке  . В соответствии с теоремой 1 плоскость
. В соответствии с теоремой 1 плоскость 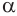 пересекает одну и другую сферы по окружности с центром
пересекает одну и другую сферы по окружности с центром  . Получили, что окружность с центром
. Получили, что окружность с центром  является общей окружностью данных сфер.
является общей окружностью данных сфер.
Других общих точек данные окружности не имеют. Допустим, что это не так. Пусть 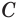 — какая-либо общая точка сфер, не принадлежащая окружности с центром
— какая-либо общая точка сфер, не принадлежащая окружности с центром  . Через точки
. Через точки 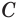 ,
, 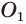 и
и 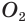 проведем плоскость, которая пересечет сферы по окружностям с центрами
проведем плоскость, которая пересечет сферы по окружностям с центрами 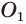 и
и 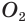 . Эти окружности пересекаются в двух точках, которые принадлежат окружности с центром
. Эти окружности пересекаются в двух точках, которые принадлежат окружности с центром  , и вместе с этим им обеим принадлежит точка
, и вместе с этим им обеим принадлежит точка 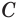 .
.
Но это противоречит утверждению о том, что две окружности имеют не более двух общих точек.
Прежде чем доказывать утверждение о поверхности сферы, обобщим утверждения о боковых поверхностях конуса, усеченного конуса и цилиндра.
Теорема 5.
Боковая поверхность конуса, усеченного конуса, цилиндра равна боковой поверхности цилиндра с той же высотой и радиусом основания, равным длине перпендикуляра, соединяющего середину образующей с точкой на оси этого тела.
Доказательство:
Пусть есть конус с вершиной 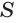 , основанием которого является круг с центром
, основанием которого является круг с центром 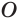 . Пусть
. Пусть 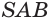 — осевое сечение конуса (рис. 186). В плоскости
— осевое сечение конуса (рис. 186). В плоскости 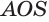 к образующей
к образующей 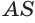 из ее середины
из ее середины 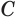 возведем перпендикуляр, который пересечет ось
возведем перпендикуляр, который пересечет ось 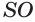 в некоторой точке
в некоторой точке 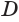 . Прямоугольные треугольники
. Прямоугольные треугольники 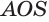 и
и 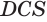 подобны, так как у них угол при вершине
подобны, так как у них угол при вершине 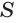 общий. Поэтому
общий. Поэтому 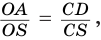 или
или 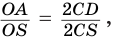 или
или 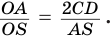
Отсюда 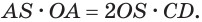
С учетом этого для боковой поверхности 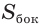 конуса будем иметь:
конуса будем иметь:
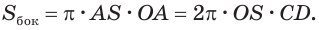
Пусть есть усеченный конус, полученный вращением прямоугольной трапеции 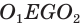 со средней линией
со средней линией 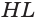 вокруг боковой стороны
вокруг боковой стороны 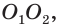 которая перпендикулярна основаниям
которая перпендикулярна основаниям 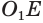 и
и 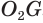 , отрезок
, отрезок 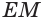 — проекция
— проекция 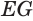 на основание
на основание 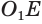 (рис. 187).
(рис. 187).
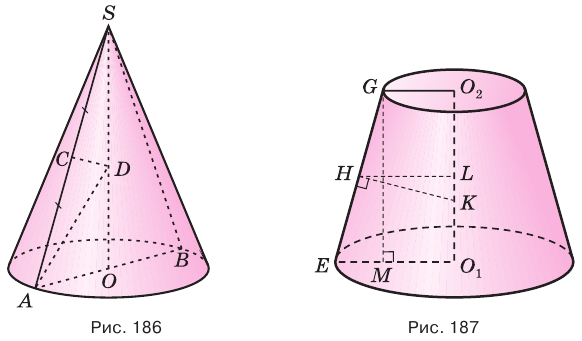
В плоскости 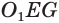 к образующей
к образующей 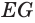 усеченного конуса из ее середины
усеченного конуса из ее середины 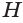 возведем перпендикуляр, который пересечет ось
возведем перпендикуляр, который пересечет ось 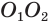 в некоторой точке
в некоторой точке 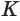 . Прямоугольные треугольники
. Прямоугольные треугольники 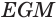 и
и 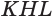 подобны, так как их стороны попарно перпендикулярны. Поэтому
подобны, так как их стороны попарно перпендикулярны. Поэтому 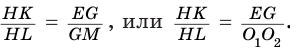
Отсюда 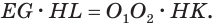
С учетом этого для боковой поверхности 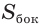 усеченного конуса будем иметь:
усеченного конуса будем иметь:
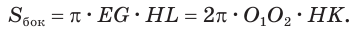
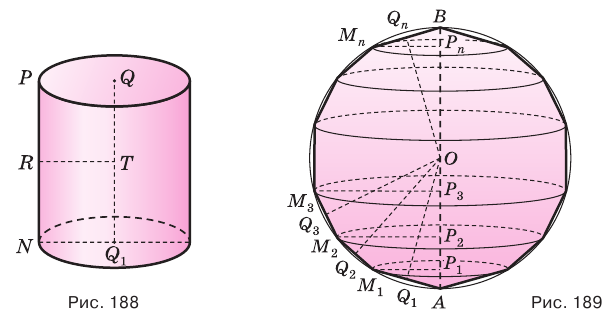
Для цилиндра утверждение очевидно (рис. 188).
Теорема 6.
Поверхность сферы равна учетверенной площади большого круга:
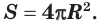
Доказательство:
Пусть есть сфера, образованная вращением полуокружности 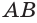 вокруг своего диаметра (рис. 189). Впишем в эту дугу ломаную
вокруг своего диаметра (рис. 189). Впишем в эту дугу ломаную 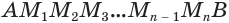 с равными звеньями и из точек
с равными звеньями и из точек 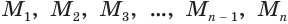 опустим перпендикуляры
опустим перпендикуляры 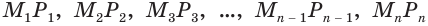 на диаметр
на диаметр 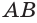 . Пусть
. Пусть  — середины звеньев ломаной. Тогда
— середины звеньев ломаной. Тогда  — серединные перпендикуляры к этим звеньям. При вращении вокруг
— серединные перпендикуляры к этим звеньям. При вращении вокруг 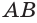 звенья ломаной будут описывать или конусы, или усеченные конусы, или цилиндр. Поэтому, в соответствии с теоремой 5, для образовавшейся поверхности
звенья ломаной будут описывать или конусы, или усеченные конусы, или цилиндр. Поэтому, в соответствии с теоремой 5, для образовавшейся поверхности 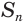 получим
получим
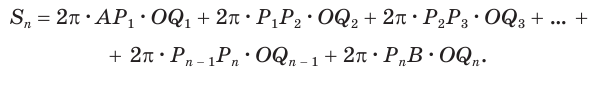
Учтем, что отрезки 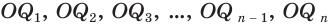 все равны друг другу:
все равны друг другу:
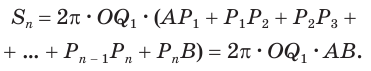
Пусть радиус сферы равен 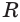 . Тогда
. Тогда 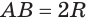 . Будем неограниченно увеличивать количество звеньев ломаной. Тогда отрезок
. Будем неограниченно увеличивать количество звеньев ломаной. Тогда отрезок 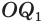 будет стремиться к радиусу сферы, а выражение
будет стремиться к радиусу сферы, а выражение 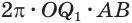 — к выражению
— к выражению 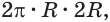 т. е. к выражению
т. е. к выражению 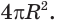 Этот предел и принимается в качестве площади поверхности сферы.
Этот предел и принимается в качестве площади поверхности сферы.
Учитывая, что 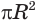 выражает площадь большого круга, получим, что поверхность сферы равна учетверенной площади большого круга.
выражает площадь большого круга, получим, что поверхность сферы равна учетверенной площади большого круга.
Уравнение сферы
Определение: Сферой радиуса R называется множество всех точек пространства, расстояние от каждой из которых до данной точки (центра) равно R.
Выведем уравнение сферы. Пусть 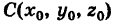 — центр сферы радиуса
— центр сферы радиуса 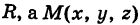 — произвольная точка, лежащая на этой сфере (рис. 204). Тогда СМ = R. По формуле расстояния между двумя точками имеем
— произвольная точка, лежащая на этой сфере (рис. 204). Тогда СМ = R. По формуле расстояния между двумя точками имеем
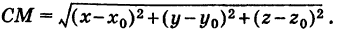
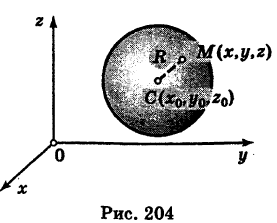
Приравнивая это выражение R, получим уравнение сферы
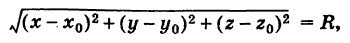
или окончательно
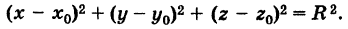
Если центр сферы совпадает с началом координат, то х0 = 0, у0 = 0, 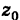 = 0 и уравнение сферы принимает вид
= 0 и уравнение сферы принимает вид
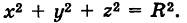
Пример:
Определить координаты центра и радиус сферы
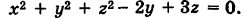
Решение:
Объединяя члены, содержащие одноименные текущие координаты, и дополняя их до полных квадратов, будем иметь
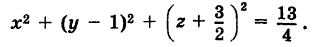
Следовательно, центр сферы находится в точке 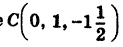 и радиус ее
и радиус ее
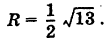
Заметим, что совокупность
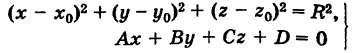
уравнений сферы и плоскости определяет окружность, по которой пересекаются плоскость и сфера (если это множество не пусто). В частности, если 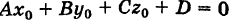 , то совокупность этих уравнений изображает окружность большого круга.
, то совокупность этих уравнений изображает окружность большого круга.
Уравнение окружности можно также писать в параметрическом виде.
Пример:
Написать параметрические уравнения меридиана сферы
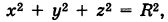
проходящего через полюсы 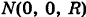 и
и 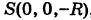 , если плоскость меридиана образует угол а с координатной плоскостью Охг (рис. 205).
, если плоскость меридиана образует угол а с координатной плоскостью Охг (рис. 205).
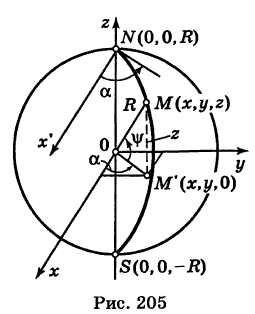
Решение:
За параметр текущей точки 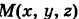 меридиана примем угол
меридиана примем угол 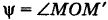 — широту этой точки, где
— широту этой точки, где 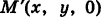 — проекция точки М на координатную плоскость Оху . Так как
— проекция точки М на координатную плоскость Оху . Так как 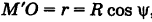 , то из рис. 205 имеем
, то из рис. 205 имеем
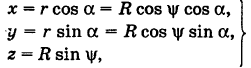
где 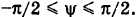
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |