Шар в геометрии - элементы, формулы, свойства с примерами

Шаром называется тело, полученное вращением круга вокруг какого-либо его диаметра (рис. 198).

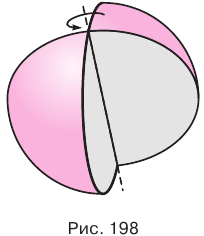
Границей шара является сфера. Центр, радиус, диаметр сферы называют также центром, радиусом, диаметром шара соответственно. Расстояние от центра шара до любой его точки не больше радиуса шара.

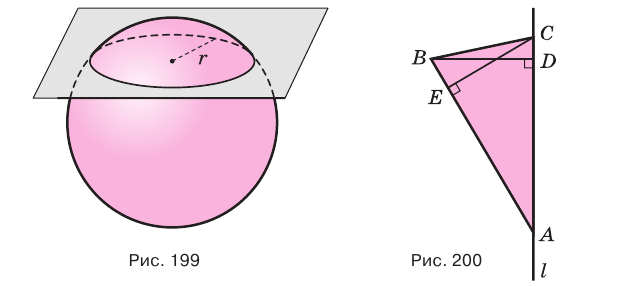
Сечением шара плоскостью является круг, радиус которого изменяется в пределах от нуля до радиуса шара (рис. 199).

Теорема 7.

Объем тела, полученного вращением треугольника вокруг прямой, лежащей в его плоскости, проходящей через его вершину и не имеющей с треугольником общих внутренних точек, равен третьей доле произведения поверхности, образованной стороной, лежащей против той вершины треугольника, которая принадлежит оси вращения, и высоты, проведенной к этой стороне.

Доказательство:

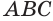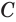Пусть есть тело, полученное вращением треугольника вокруг прямой , которая лежит в плоскости треугольника, проходит через его вершину и не имеет с треугольником общих внутренних точек. Пусть вершина принадлежит оси , а 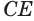— высота, проведенная к стороне 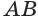против вершины 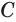. Докажем, что объем 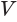тела вращения равен

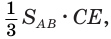
где обозначает поверхность, образованную вращением стороны .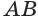

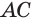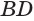Пусть сторона лежит на оси вращения и — перпендикуляр, опущенный из вершины 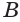на прямую (рис. 200). Тогда стороны 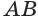и 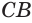опишут поверхности двух конусов с общим радиусом 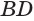и высотам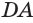и и 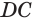соответственно. Для объема 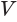тела вращения получим:

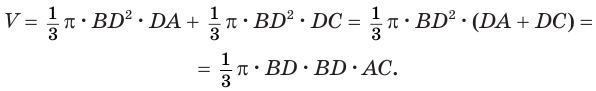
Теперь обратим внимание на то, что 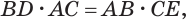так как одно и другое произведения выражают удвоенную площадь треугольника 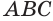. Поэтому

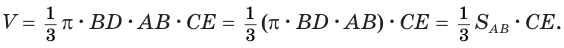
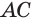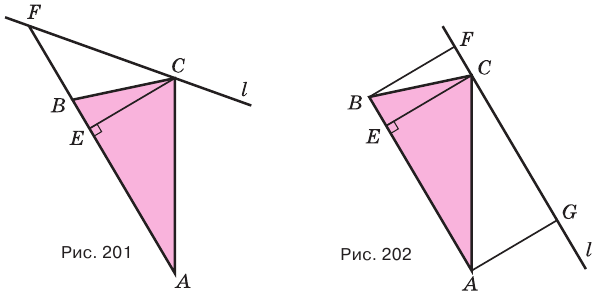
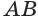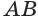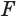Пусть сторона не лежит на оси вращения , а сторона не параллельна этой оси (рис. 201). Тогда прямая пересекает ось в некоторой точке , и объем 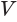тела вращения равен разности объемов тел, полученных вращением треугольников 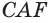и 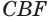. Учитывая это и то, что сторона 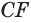этих треугольников принадлежит оси вращения, для объема получим:

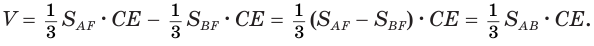
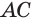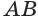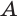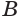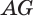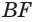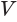Пусть сторона не лежит на оси вращения , а сторона параллельна этой оси (рис. 202). Из точек и опустим перпендикуляры и на ось вращения . Объем тела вращения можно получить, вычитая из объема цилиндра, полученного вращением прямоугольника 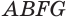, объемы двух конусов, полученных вращением треугольников 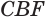и 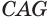. Поэтому:

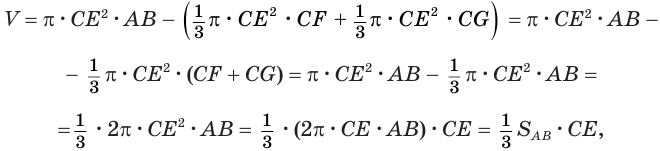
так как выражение 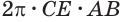задает поверхность, образованную вращением стороны .

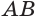Теорема 8.

Объем тела, полученного вращением кругового сектора вокруг прямой, проходящей через его центр, лежащей в его плоскости и не имеющей с ним общих внутренних точек, равен третьей доле произведения радиуса сектора и поверхности, образованной при вращении дуги сектора.

Доказательство:

Пусть имеется тело, полученное вращением кругового сектора 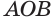с радиусом 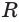вокруг прямой , проходящей через центр сектора 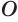и не имеющей с ним общих внутренних точек. Впишем в этот сектор ломаную 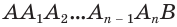с равными звеньями (рис. 203). Объем тела, полученного вращением этой ломаной вокруг прямой , равен сумме объемов тел, полученных вращением треугольников 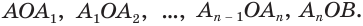Пусть 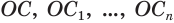- высоты этих треугольников. Применив теорему 7, получим:

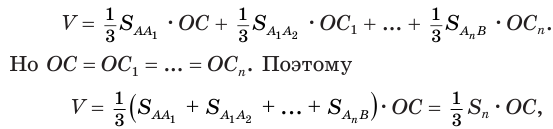
где 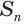— поверхность, образованная при вращении 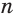-звенной ломаной.

Будем увеличивать количество сторон ломаной, вписанной в круговой сектор 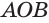. Тогда высота 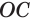будет стремиться к радиусу 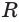, а поверхность 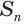— к поверхности 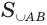. Поэтому объем 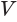стремится к выражению 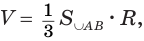которое и принимается в качестве объема тела, образованного вращением кругового сектора 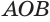вокруг прямой , проходящей через центр сектора 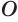и не имеющей с ним общих внутренних точек.

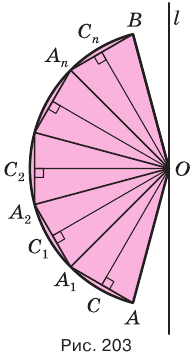
Следствие 1. Объем шара равен третьей доле произведения его поверхности и радиуса:

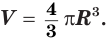
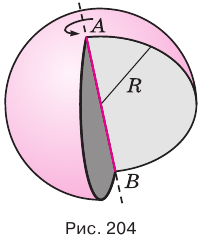
Действительно, шар с радиусом 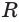можно рассматривать как тело, образованное вращением сектора-полукруга вокруг диаметра (рис. 204). Тогда соответствующая окружность образует сферу. В соответствии с теоремой 8 получим:

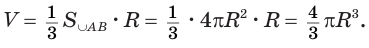
Рассмотрим комбинации шара с другими телами.

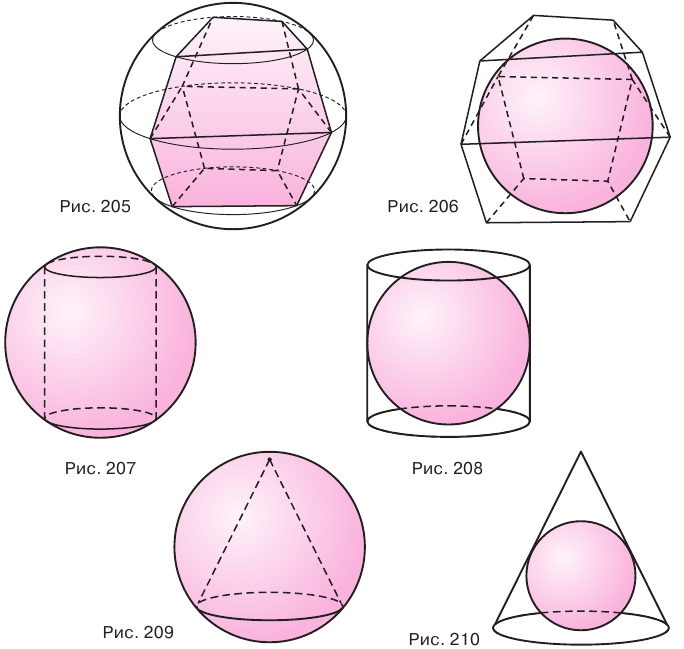
Вписанным в шар многогранником называется многогранник, все вершины которого лежат на соответствующей сфере (рис. 205). Описанным около шара многогранником называется многогранник, все грани которого касаются соответствующей сферы (рис. 206).

Вписанным в шар цилиндром называется цилиндр, окружности оснований которого принадлежат соответствующей сфере (рис. 207). Описанным около шара цилиндром называется цилиндр, основания и все образующие которого касаются соответствующей сферы (рис. 208).

Вписанным в шар конусом называется конус, вершина и окружность основания которого принадлежат соответствующей сфере (рис. 209). Описанным около шара конусом называется конус, основание и все образующие которого касаются соответствующей сферы (рис. 210).

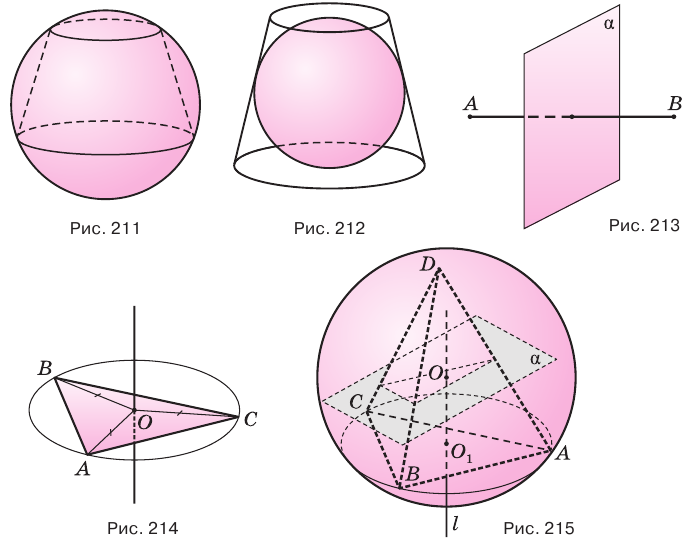
Вписанным в шар усеченным конусом называется усеченный конус, окружности оснований которого принадлежат соответствующей сфере (рис. 211). Описанным около шара усеченным конусом называется конус, основания и все образующие которого касаются соответствующей сферы (рис. 212).

Теорема 9.

Около каждой треугольной пирамиды можно описать единственный шар.

Доказательство:

Сначала обратим внимание на то, что геометрическое место точек, равноудаленных от кондов отрезка, есть плоскость, проходящая через середину отрезка и перпендикулярная ему (рис. 213). Она называется серединной плоскостью отрезка. Геометрическим местом точек, равноудаленных от вершин треугольника, является прямая, проходящая через центр описанной около треугольника окружности и перпендикулярная его плоскости (рис. 214).

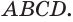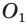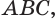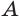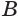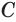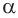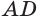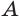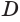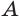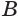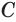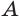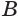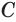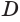Пусть есть треугольная пирамида Через центр окружности, описанной около грани проведем прямую , перпендикулярную плоскости этой грани (рис. 215). Все точки прямой равноудалены от вершин , , . Построим серединную плоскость отрезка , она пересечет прямую в некоторой точке . Вершины и равноудалены от точки . А поскольку вершины , , равноудалены от точки , то все четыре вершины , , , равноудалены от точки . Получили, что все вершины пирамиды 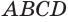принадлежат сфере с центром , а это означает, что шар с центром и радиусом 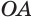и есть шар, описанный около пирамиды .

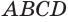Единственность найденного шара следует из того, что прямая и ее точка определяются однозначно.

Следствие 2. Четыре точки пространства, не лежащие в одной плоскости, определяют единственную сферу, единственный шар.

Теорема 10.

В каждую треугольную пирамиду можно вписать единственный шар.

Доказательство:

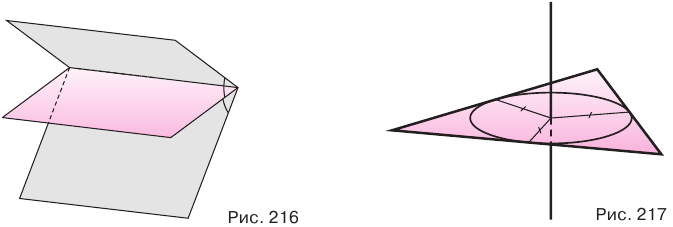
Сначала обратим внимание на то, что геометрическим местом точек, равноудаленных от граней двугранного угла, является полуплоскость, граница которой совпадает с ребром двугранного угла и которая делит этот угол пополам (рис. 216). Она называется биссекторной плоскостью угла. Геометрическим местом точек, равноудаленных от сторон треугольника, является прямая, проходящая через центр вписанной в треугольник окружности и перпендикулярная его плоскости (рис. 217).

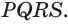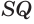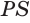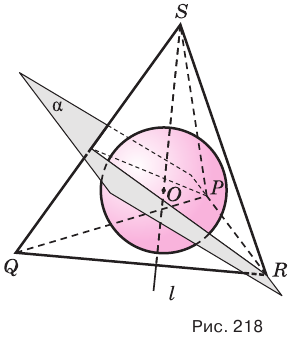
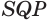Пусть есть треугольная пирамида Пусть биссекторные плоскости двугранных углов и пересекаются по прямой (рис. 218). Каждая точка прямой равноудалена от плоскостей и 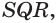а также от плоскосте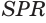й и 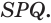Поэтому каждая точка прямой равноудалена от боковых граней пирамиды. Построим биссекторную плоскость 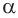двугранного угла 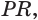она пересечет прямую в некоторой точке . 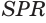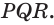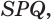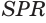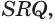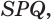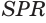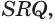Эта точка равноудалена от граней и А поскольку точка как точка прямой равноудалена от граней , то все четыре грани , 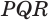равноудалены от точки . Получили, что все грани пирамиды 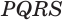касаются сферы с центром , а это означает, что шар с центром и радиусом 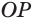и есть шар, вписанный в пирамиду .

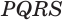Единственность найденного шара следует из того, что прямая и ее точка определяются однозначно.

Теорема 11.

Объем описанного около шара многогранника равен третьей доле произведения полной поверхности многогранника и радиуса шара.

Доказательство:

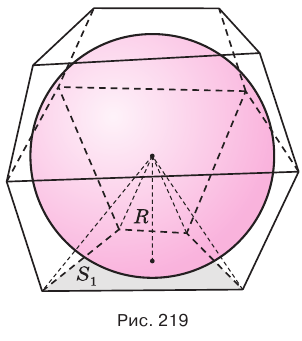
Пусть есть многогранник, который описан около шара (рис. 219). Центр шара соединим со всеми вершинами многогранника. Если многогранник имеет 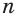граней, то образуется 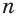пирамид, для которых центр шара является общей вершиной, основания составляют поверхность многогранника, а сами пирамиды вместе составят многогранник. Основания высот этих пирамид совпадают с точками касания, а поэтому сами высоты все равны радиусу 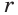шара.

Пусть площади граней многогранника равны 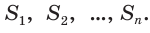Тогда для объема 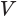многогранника, который равен сумме объемов пирамид, получим:

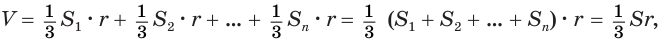
где 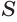— полная поверхность многогранника.