
Принцип и метод наложения
Метод наложения:
Используя метод контурных токов, можно получить обобщённое уравнение по расчёту любого 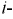
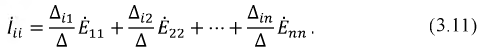
Сомножитель перед любой ЭДС имеет размерность 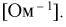
Это уравнение применимо для любого реального тока в ветви, так как всегда возможно выбрать систему независимых контуров так, чтобы ток в ветви был численно равен контурному току. Если в уравнении (3.8) учесть, что контурная ЭДС - сумма всех ЭДС контура, то, перегруппировав слагаемые таким образом, чтобы каждая ЭДС умножалась на соответствующую сумму слагаемых вида 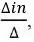 получим уравнение для тока ветви в виде:
получим уравнение для тока ветви в виде:
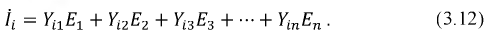
В правой части уравнения (3.12) имеем сумму слагаемых - токов, созданных каждой из ЭДС в отдельности.
Принцип наложения: ток любой  ой ветви равен алгебраической сумме токов, созданных каждой из ЭДС цепи в отдельности.
ой ветви равен алгебраической сумме токов, созданных каждой из ЭДС цепи в отдельности.
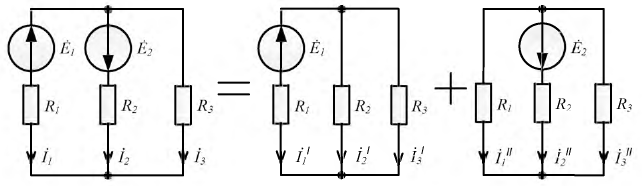
Рис. 3.3. Иллюстрация принципа наложения
На сформулированном принципе базируется метод наложения, суть которого состоит в следующем: в исходной электрической цепи поочерёдно закорачиваются все источники ЭДС, кроме одного, и производится расчет частичных токов в ветвях любым из известных методов. Для определения реальных токов в исходной цепи производится алгебраическое суммирование этих частичных токов:
Метод наложения
В линейной электрической цепи, содержащей источники э. д. с., контурные токи (и соответственно токи в ветвях) представляют собой линейные функции контурных э. д. с. Математически они выражаются формулой (7-4):
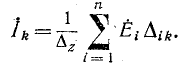
Физический смысл этой формулы заключается в том, что ток в любом контуре линейной электрической цепи может быть получен как алгебраическая сумма токов, вызываемых в этом контуре каждой из э. д. с. в отдельности.
Метод расчета токов, основанный на определении токов в одном и том же контуре (или ветви) при поочередном воздействии э. д. с. и последующем алгебраическом сложении этих токов, называется методом наложения.
При определении частичных слагающих токов по методу наложения необходимо считать включенными внутренние сопротивления тех источников э. д. с., которые принимаются отсутствующими при вычислении слагающих токов. Если в цепи заданы идеальные источники э. д. с., т. е. внутренние сопротивления источников равны нулю, то при определении токов, вызываемых какой-либо э. д. с., все остальные источники э. д. с. закорачиваются.
В свою очередь в линейной электрической цепи, содержащей источники тока, узловые напряжения (и соответственно напряжения на ветвях) представляют собой линейные функции задающих токов источников. Математически они выражаются- формулой (7-6):
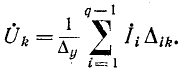
Физический смысл этой формулы заключается в том, что узловое напряжение для любого узла линейной электрической цепи может быть получено как алгебраическая сумма напряжений, вызываемых в этом узле каждым из задающих
токов в отдельности. Таким образом, формула (7-6), так же как и (7-4), представляет собой математическую запись метода наложения, справедливого для линейных электрических цепей.
При определении частичных слагающих узловых напряжений по методу наложения необходимо считать включенными внутренние проводимости тех источников тока, которые принимаются отсутствующими при вычислении слагающих напряжений. Если источники тока заданы без внутренних проводимостей, т. е. проводимости их равны нулю, то при пользовании методом наложения ветви с неучтенными источниками тока разрываются.
Если в линейной электрической цепи заданными являются одновременно источники э. д. с. и источники тока, то метод наложения применим и в этом случае. Например, ток в каком-либо контуре данной цепи может быть получен в результате алгебраического сложения токов, вызываемых в этом контуре поочередным действием источников э. д. с. и тока. При этом отсутствующие источники э.д.с. заменяются внутренними сопротивлениями, а отсутствующие источники тока — внутренними проводимостями.
Пример 7-4.
Пользуясь методом наложения, определить ток в ветви  схемы рис. 7-4,
схемы рис. 7-4,
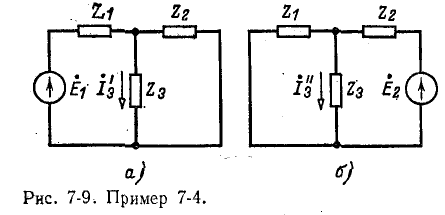
Искомый ток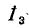 определяется как сумма токов
определяется как сумма токов 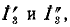 проходящих через, ветвь
проходящих через, ветвь 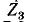 под воздействием источников э. д. с.
под воздействием источников э. д. с. 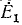 (рис. 7-9, а) и
(рис. 7-9, а) и 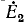 (рис. 7-9, б), взятых порознь. .
(рис. 7-9, б), взятых порознь. .
Токи 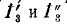 суммируются, а не вычитаются, так как положительные направления их выбраны совпадающими:
суммируются, а не вычитаются, так как положительные направления их выбраны совпадающими: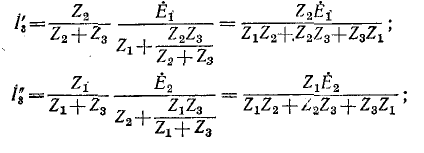
следовательно,
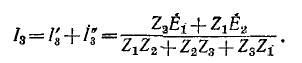
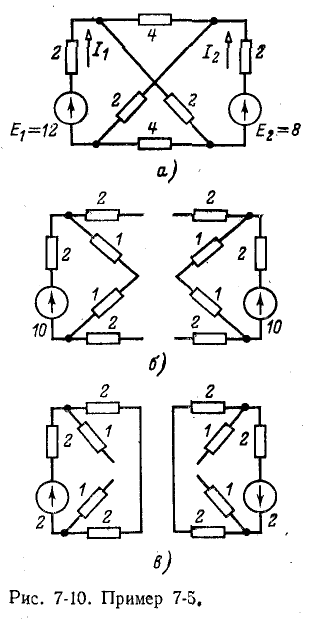
Пример 7-5.
Задана симметричная схема с неравными э. д. с.: 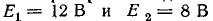 (рис. 7-10, а). Значения сопротивлений (в омах) указаны по схеме, тив, что
(рис. 7-10, а). Значения сопротивлений (в омах) указаны по схеме, тив, что 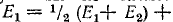
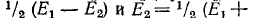
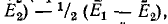 , можно вместо заданной схемы рассмотреть две симметричные схемы, в каждой из которых э. д. с. источников равны. В первой схеме источники имеют э. д. с.
, можно вместо заданной схемы рассмотреть две симметричные схемы, в каждой из которых э. д. с. источников равны. В первой схеме источники имеют э. д. с.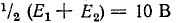 и полярность их одинакова; во второй схеме источники имеют э. д. с.
и полярность их одинакова; во второй схеме источники имеют э. д. с. 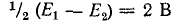 и полярность различна.
и полярность различна.
Пользуясь методикой, описанной, произведем соответствующие рассечения и замыкания накоротко по оси симметрии (рис. 7-10, 6 и в).
Искомые токи найдутся методом наложения:
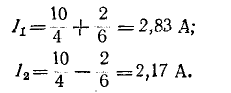
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |