
Входные и взаимные проводимости
Входные и взаимные проводимости:
Пусть дана некоторая электрическая цепь, содержащая единственный источник ЭДС в 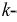
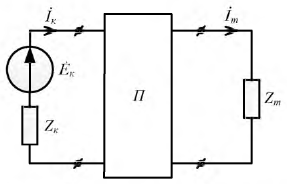
Рис. 3.4. Схема пассивного четырехполюсника
Определим 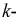 й и
й и 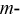 й токи. Используя уравнение (3.12), запишем выражение для
й токи. Используя уравнение (3.12), запишем выражение для 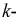 то и
то и 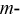 го токов:
го токов:
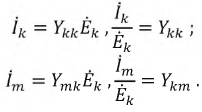
Если 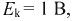 то
то 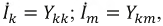 т.е., токи
т.е., токи 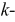 й и
й и 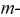 й ветвей численно равны своим проводимостям.
й ветвей численно равны своим проводимостям. 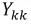 - входная проводимость
- входная проводимость 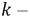 ой ветви.
ой ветви. 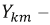 взаимная проводимость
взаимная проводимость 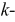 ой и
ой и 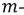 ой ветвей. Рассмотрим пример определения входных и взаимных проводимостей (рис. 3.5).
ой ветвей. Рассмотрим пример определения входных и взаимных проводимостей (рис. 3.5).
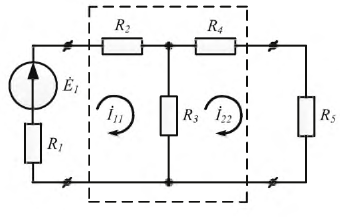
Рис. 3.5. Схема замещения пассивного четырехполюсника
Представим пассивный четырехполюсник в виде схемы рис. 3.5 и составим для нее уравнения по методу контурных токов.
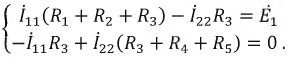
Тогда входная проводимость первой ветви будет:
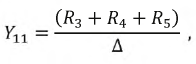
а взаимная проводимость первой и второй ветвей:
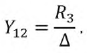
Свойство взаимности
Рассмотрим еще одно важное свойство, имеющее место в линейных электрических цепях. Оно базируется на понятиях входных и взаимных проводимостей.
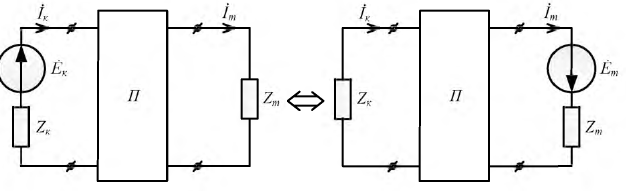
Используя понятие взаимных проводимостей, можно выразить токи в первой и второй схемах рис. 3.6 следующим образом:
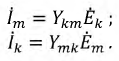
Докажем, что взаимные проводимости 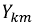 и
и 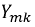 равны. Пусть для некоторой многоконтурной схемы составлена система уравнений по методу контурных токов, и её главный определитель имеет вид:
равны. Пусть для некоторой многоконтурной схемы составлена система уравнений по методу контурных токов, и её главный определитель имеет вид:
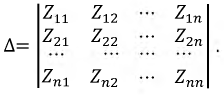
Этот определитель всегда симметричен относительно главной диагонали, проходящей через элементы 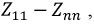 т.к. любой элемент
т.к. любой элемент 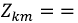
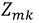 (сопротивления, расположенные на границе
(сопротивления, расположенные на границе 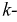 ого и
ого и 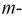 ого контуров). У такого определителя строка
ого контуров). У такого определителя строка 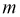 не отличается от столбца
не отличается от столбца 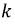 и поэтому алгебраические дополнения, полученные вычеркиванием
и поэтому алгебраические дополнения, полученные вычеркиванием 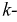 ой строки и
ой строки и 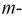 ого столбца и наоборот, равны. Следовательно,
ого столбца и наоборот, равны. Следовательно,
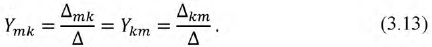
Пусть 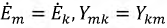 и
и 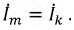
Свойство взаимности: если ЭДС 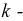 ой ветви вызывает в
ой ветви вызывает в 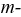 ой ветви ток
ой ветви ток 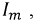 то, будучи перенесенным в
то, будучи перенесенным в 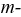 ю ветвь, этот же источник вызовет ток той же амплитуды и фазы в
ю ветвь, этот же источник вызовет ток той же амплитуды и фазы в 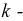 ой ветви.
ой ветви.
Цепи, обладающие такими свойствами, носят название обратимых цепей. Все линейные цепи обратимы.
Входные и передаточные проводимости и сопротивления
В электротехнике, радиотехнике и теории автоматического регулирования широко используются понятия о входных и передаточных функциях.
Условимся называть источник э. д. с. независимым или автономным (самостоятельным), если э. д. с. источника не зависит от напряжений и токов в цепи.
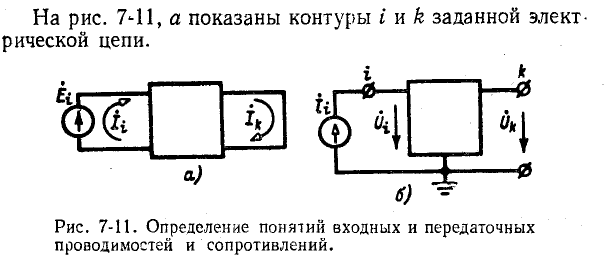
Пусть в какую-либо ветвь контура электрической цепи включен независимый источник э. д. с. 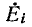 (рис. 7-11, а), причем данная ветвь не является общей, а принадлежит
(рис. 7-11, а), причем данная ветвь не является общей, а принадлежит
только контуру i. Если вся остальная часть электрической цепи не содержит независимых источников электрической энергии, то в соответствии с формулой (7-4) заданная э. д. с. 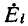 вызовет в данном контуре i и в каком-либо другом контуре k токи
вызовет в данном контуре i и в каком-либо другом контуре k токи

и

Отношение контурного тока к э. д. с., действующей в том же контуре, при отсутствии независимых источников во всех остальных контурах называется входной проводимостью электрической цепи:

В свою очередь отношение контурного тока к э. д. с., действующей в другом контуре, при отсутствии независимых источников во всех остальных контурах называется передаточной (или взаимной) проводимостью контуров:
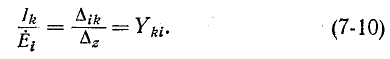
Элементами определителя системы и алгебраических дополнений в выражениях (7-9) и (7-10) служат собственные и общие сопротивления контуров заданной электрической цепи. Определитель 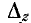 имеет размерность сопротивления в степени n, где n — порядок определителя (равный числу независимых контуров данной цепи); алгебраические дополнения
имеет размерность сопротивления в степени n, где n — порядок определителя (равный числу независимых контуров данной цепи); алгебраические дополнения 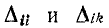 имеют размерность сопротивления в степени n — 1. В результате деления алгебраического дополнения на определитель системы получается величина, имеющая размерность проводимости.
имеют размерность сопротивления в степени n — 1. В результате деления алгебраического дополнения на определитель системы получается величина, имеющая размерность проводимости.
На основании (7-9) и (7-10) заключаем, что входная и передаточная проводимости численно равны токам в контурах i и k, когда в контуре i действует э. д. с., равная 1 В.
С учетом обозначений (7-9) и (7-10) выражения для токов (7-4) принимают вид:

Аналогичные рассуждения могут быть проведены и в отношении узлов i и к электрической цепи в предположении, что к узлу i подключен независимый источник тока
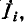 , а вся остальная часть цепи не содержит независимых источников (рис. 7-11, 6). В соответствии с (7-6) заданный ток
, а вся остальная часть цепи не содержит независимых источников (рис. 7-11, 6). В соответствии с (7-6) заданный ток 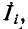 обусловит появление узловых напряжений для узлов i и к:
обусловит появление узловых напряжений для узлов i и к:

и

Отношение напряжения в узле к току, заданному в том же узле, при отсутствии в схеме других независимых источников называется входным сопротивлением электрической цепи:

соответственно отношение напряжения в узле к току, заданному в другом узле, при отсутствии в схеме других источников называется передаточным (или взаимным) сопротивлением узлов:

Элементами определителя системы и алгебраических дополнений в (7-14) и (7-15) служат собственные и общие проводимости узлов заданной электрической цепи.
 Источник тока называется независимым, или автономным, если ток источника не зависит от напряжений и токов в цепи.
Источник тока называется независимым, или автономным, если ток источника не зависит от напряжений и токов в цепи.
Определитель 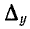 имеет размерность проводимости в степени m, где m— порядок определителя (на единицу меньший числа узлов в заданной схеме); алгебраические дополнения
имеет размерность проводимости в степени m, где m— порядок определителя (на единицу меньший числа узлов в заданной схеме); алгебраические дополнения 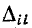 и
и 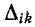 имеют размерность проводимости в степени m— i. В результате деления алгебраического дополнения на определитель системы получается величина, имеющая размерность сопротивления.
имеют размерность проводимости в степени m— i. В результате деления алгебраического дополнения на определитель системы получается величина, имеющая размерность сопротивления.
На основании (7-14) и (7-15) заключаем, что входное и передаточное сопротивления узлов численно равны напряжениям в узлах i и k (относительно базисного узла), когда в узле i задан ток, равный 1 А.
С учетом обозначений (7-14) и (7-15) выражения для напряжений (7-6) принимают вид:
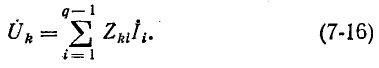
Следует иметь в виду, что входным сопротивлением может также называться величина, обратная выражению (7-9), а входной проводимостью — величина, обратная выражению (7-14).
Очевидно, что для одной и той же пары выводов электрической цепи, не содержащей источников, величины 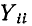 и
и 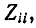 определяемые, из (7-9) и (7-14), взаимно обратны, т. е.
определяемые, из (7-9) и (7-14), взаимно обратны, т. е.
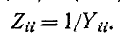
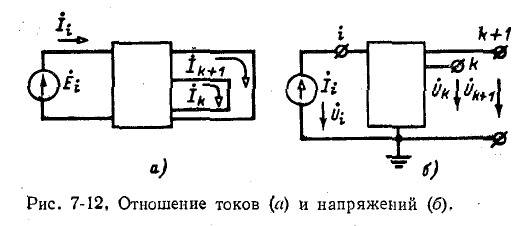
Отношение двух контурных токов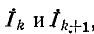 вызываемых в контурах k и k + 1 источником э. д. с.
вызываемых в контурах k и k + 1 источником э. д. с. 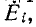 , включенным в контур i (рис. 7-12, а), определяется на основании (7-10), отношением соответствующих передаточных проводимостей, а именно:
, включенным в контур i (рис. 7-12, а), определяется на основании (7-10), отношением соответствующих передаточных проводимостей, а именно:
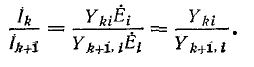
Аналогично отношение двух узловых напряжений и 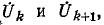 обусловливаемых в узлах k и k + 1 источником тока
обусловливаемых в узлах k и k + 1 источником тока 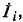 заданным в узле i (рис. 7-12, б), определяется на основании (7-15) отношением соответствующих передаточных сопротивлений:
заданным в узле i (рис. 7-12, б), определяется на основании (7-15) отношением соответствующих передаточных сопротивлений:
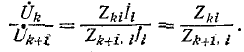
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |