Условия равновесия системы сходящихся сил в аналитической форме в теоретической механике

Содержание:

Условия равновесия системы сходящихся сил в аналитической форме:

Проекцией силы на ось называют скалярную величину, равную произведению модуля силы на косинус угла между положительным направлением оси и направлением силы

Проекция силы на ось

C только что рассмотренным понятием «составляющая силы по оси» тесно соприкасается другое важное понятие—«проекция силы на ось». 

Изобразим силу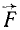

ab = AB' = AB cos а.

Для получения проекции мы умножали на cos а не вектор, а его модуль, его абсолютную величину. Проекция силы на ось не является вектором, поскольку она не имеет собственного направления, а вполне определяется направлением оси, величиной проекции (длиной ab) и знаком « + » или «—». Проекция ab силы AB положительна (+ab), если направление вектора силы составляет с положительным направлением оси острый угол (рис. 14, а), и отрицательна (—ab), если—тупой (рис. 14, б). Мы подчеркиваем, что проекция вектора на ось не имеет своего направления, тем не менее условимся, что положительная проекция «направлена» в сторону положительного направления оси, а отрицательная — в противоположную сторону, и иногда на чертежах будем изображать стрелками проекции вектора на ось.

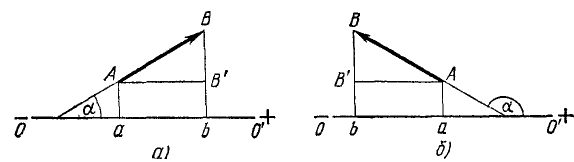
Рис. 14

Напомним, что всякую величину, определяемую числом и только числом, называют скаляром. Например, плотность, температура, масса являются скалярами. Скалярами первого рода называют величины, не зависящие от направления осей координат. Если же число, определяющее рассматриваемую величину, меняет знак при перемене направления осей координат на обратные, то скаляр является скаляром второго рода (см., например, Аппель. Теоретическая механика). Следовательно, проекция силы на ось есть скаляр второго рода.

Направляющим косинусом называют косинус угла между положительным направлением оси и направлением вектора; он выражается отношением проекции вектора на эту ось к модулю вектора и по знаку совпадает со знаком проекции

Направляющий косинус

Знак проекции определяется знаком косинуса угла между направлением вектора и положительным направлением оси, этот косинус называют направляющим косинусом. Если этот угол острый, то направляющий косинус положителен и проекция вектора на ось положительна, если же угол тупой, то направляющий косинус отрицателен и проекция вектора на ось тоже отрицательна.

Часто требуется по заданным проекциям вектора на координатные оси определять величины и знаки направляющих косинусов. Как видно из предыдущего равенства, выражения является существенно положительной величиной. В дальнейшем мы не всегда будем ставить эти вертикальные черточки, помня, что знаменатель в выражении направляющего косинуса является положительным.

По этой формуле можно определять не только направляющие косинусы вектора силы, но и направляющие косинусы всякого другого вектора (скорости, ускорения и πp.). Во всех отделах нашего курса направляющим косинусам отведена значительная роль.

Углы, составляемые каким-либо вектором с осями х, y и z, мы будем обозначать соответственно буквами α, β и γ с индексом вектора. Например, углы, составляемые вектором F с осями координат, будем обозначать α_F, β_F, γ_F∙. Если проекции силы 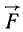на оси координат обозначать через X, Y и Z, то

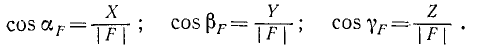 (3)

Практически при решении задач для определения проекции силы на ось обычно умножают модуль силы на косинус острого угла между осью (ее положительным или отрицательным направлением) и линией действия силы и приписывают проекции знак «+» или «—» в зависимости от того, «направлена» ли проекция в сторону положительного или в сторону отрицательного направления оси.

Проекция вектора на плоскость является вектором

Проекция силы на плоскость

В отличие от проекции силы на ось проекция силы на плоскость является вектором и имеет собственное направление на плоскости.

Чтобы спроецировать силу 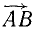на плоскость, надо опустить на плоскость перпендикуляры Ab и Bb (рис. 15) из начала А и из конца В вектора силы; полученный вектор 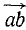, лежащий в плоскости, является проекцией силы на плоскость:

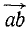=пp. .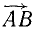

Модуль проекции равен произведению модуля силы на косинус угла наклона вектора силы к плоскости:

αb = AB cos a.

Проекция равнодействующей равна сумме проекций составляющих сил

Теорема о проекции равнодействующей

Покажем, что проекция равнодействующей на плоскость равна геометрической сумме проекций составляющих.

Дан пучок сил, представленный силовым многоугольником OAEKL, и дана некоторая плоскость (рис. 16). Опуская перпендикуляры Oo, Aa, Ее, Kk и Ll на плоскость из вершин силового многоугольника, найдем проекции составляющих сил на плоскость: проекция 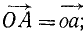 проекция  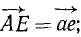проекция 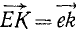проекция 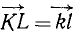. Складывая все проекции, получим 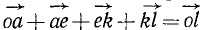. Но вектор 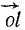является проекцией равнодействующей OL на ту же плоскость: проекция .

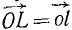Сопоставляя между собой два последних равенства, найдем, что проекция равнодействующей на плоскость равна сумме проекций составляющих на ту же плоскость. Проекция сил на плоскость — вектор, поэтому сумма геометрическая.

Напротив, проекции силы на ось—скалярные величины, а потому проекция равнодействующей на ось равна алгебраической сумме проекций составляющих на ту же ось. Пусть дан пучок сил, представленный силовым многоугольником OAEKL, и дана ось (рис. 17). Опуская перпендикуляры Oo, Aa, Ее, Kk и Ll на ось из вершин силового многоугольника, найдем проекции составляющих сил на ось: проекция 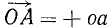; проекция 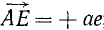; проекция 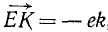; проекция  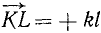. Складывая все проекции, получим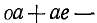 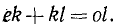. Но ol является проекцией равнодействующей 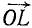на ту же ось: проекция 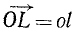. Остается лишь сопоставить между собой два последних равенства.

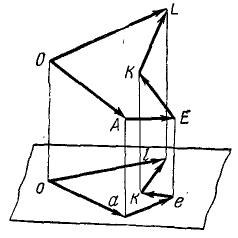
Рис. 16

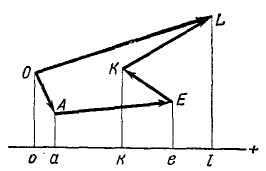
Рис. 17

Величину и направление равнодействующей пучка сил можно определить по суммам проекций составляющих на взаимно перпендикулярные оси.

Если угол, составляемый равнодействующей с данной осью, известен, то, поделив сумму проекций составляющих на косинус этого угла, можно определить численную величину равнодействующей. Если же, как это обычно и бывает, направление равнодействующей неизвестно, то для определения равнодействующей составляют суммы проекций всех составляющих на пересекающиеся (обычно взаимно перпендикулярные) оси.

Пусть дана система сил, сходящихся в одной точке. Для простоты рассуждений предположим, что все эти силы лежат в одной плоскости. Проведем в этой плоскости декартову систему координат хОу и спроецируем все силы на оси Ox и Оу.

Обозначим проекцию силы 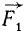на ось абсцисс через X₁, а на ось ординат—через Y₁; проекции силы  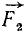обозначим теми же буквами с индексом 2 и т. д. Сумму проекций всех сил на ось абсцисс обозначим символом 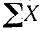, a на ось ординат—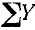. Проекция равнодействующей на какую-либо ось равна алгебраической сумме проекций составляющих на ту же ось, и мы можем написать равенства

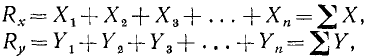     (4)

где R_x и R_y означают проекции равнодействующей на оси координат. Теперь мы можем найти величину равнодействующей:

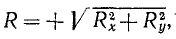
или 

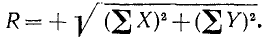      (5^/)

Направление равнодействующей можно определить по направляющим косинусам:

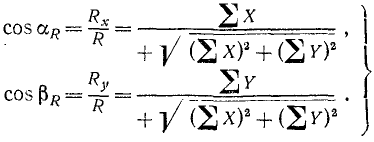    (6^/)

Если силы системы не лежат в одной плоскости, то, спррецировав силы на три координатные оси, получим

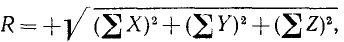       (5)

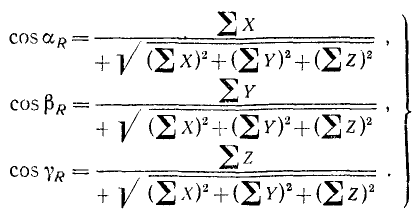    (6)

Знак направляющего косинуса определяется знаком числителя. Возведя равенства (6) или (6') в квадрат и сложив, убедимся, что сумма квадратов направляющих косинусов равна единице:

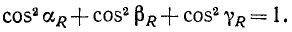    (7)

Задача №1

Найти равнодействующую 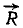двух сил 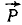и 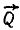по Зн каждая, направленных под углом 120° друг к другу (см. рис. 3, в).

Решение. Примем точку приложения сил за начало координат, направим ось Ox по силе Q, а ось Oy к ней —перпендикулярно. Как видно из чертежа, направляющие косинусы складываемых сил таковы:

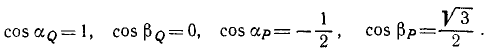
Найдем проекции равнодействующей по формулам (4) и модуль равнодействующей по (5'):

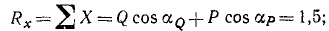
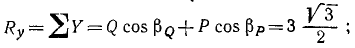
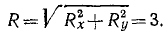
Ее направление определим по направляющим косинусам (6'):

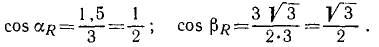
Ответ.R = 3н и направлена под углом 60° к силам.

Для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнялись нулю суммы проекций всех сил на оси координат

Условия равновесия пучка сил в аналитической форме. Как было показано в § 3, при равновесии системы сходящихся сил ее равнодействующая равна нулю. Если пучок сил является плоским, то из (5') следует

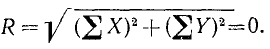
Сумма квадратов двух величин может равняться нулю только в случае, если равна нулю каждая из этих величин, а потому

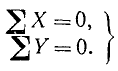     (8)

Эти равенства называют условиями равновесия плоской системы сходящихся сил в аналитической форме. Они являются необходимыми и достаточными условиями.

Если же пучок сил не лежит в одной плоскости, но является уравновешенной системой, то путем аналогичных рассуждений мы выведем условия равновесия пространственной системы сходящихся сил в аналитической форме:

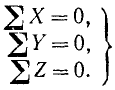     (9)

Если условия равновесия (8) и (9) содержат неизвестные величины, то их называют уравнениями равновесия сходящихся сил.

• Заказать решение задач по теоретической механике

Задача №2

Нить с грузами P и Q на концах перекинута через блоки А и В, находящиеся на одной горизонтали (рис. 18, α). В точке О нити, находящейся между блоками, привязан груз G = 27,3 н. При равновесии системы ветвь OA образует с горизонталью угол 60°, а ветвь OB— угол 45°. Пренебрегая трением в блоках, определить величину грузов P и Q.

Решение. Равновесие какого объекта надо рассмотреть для решения задачи? Ответим на этот вопрос. Требуется определить веса грузов P и Q. Веса грузов приложены к этим грузам и направлены вертикально вниз. Каждый груз натягивает нить силой, равной своему весу. Блок меняет направление нити, а следовательно, и направление силы натяжения нити, не меняя ее величины. Силы, по модулю равные P и Q и направленные по OA и OB, пересекаются в точке 0, где приложена и заданная сила G (рис. 18, б). Поэтому для решения задачи надо рассмотреть равновесие точки О.

Какие же силы действуют на точку О? На нее действуют сила G; натяжение P ветви OA-, натяжение Q ветви OB. Веса грузов PhQ, приложенные к этим грузам, учитывать не надо, потому что они не приложены к точке О.

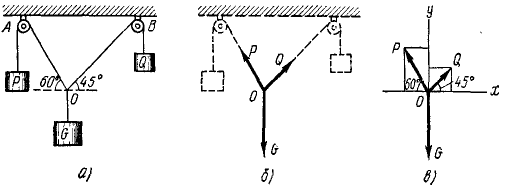
Рис. 18

Для изучения равновесия сил, приложенных к точке О, можно построить силовой многоугольник или составить уравнения равновесия. Выберем второй путь. Построим систему координат с началом в точке О (рис. 18, в), спроецируем силы на оси и составим уравнения равновесия.
Для проекций на ось Ox имеем

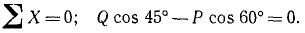
Знак проекции Q положительный, потому что она направлена в положительном направлении оси Ox (вправо). Знак у проекции P отрицательный, так как она направлена в отрицательном направлении оси Ох. Проекция силы G на ось Ox равна нулю.
Аналогично получаем

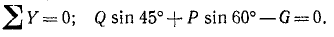
Проекции P и Q на ось Oy положительны, так как направлены в положительном направлении оси. Проекция G отрицательна, так как направлена вниз. Подставляя числовые значения и решая уравнения, получаем ответ.
Ответ. P = 20 н, Q = 14,1 н.

Задача №3

Земляная насыпь подпирается вертикальной каменной стеной АВ. Найти необходимую толщину стены а, предполагая, что давление земли на стену направлено горизонтально, приложено на 1/3 ее высоты и равно 6 тонн на метр длины стены; удельный вес кладки 2 Г/см³. Стена должна быть рассчитана на опрокидывание вокруг ребра А (рис. 19, а).

Решение. Первый вопрос: равновесие какого тела надо рассмотреть?
Нужно рассмотреть равновесие каменной стены АВ.

Второй вопрос: какие силы действуют на рассматриваемое тело?

На стену действуют следующие силы (рис. 19, б):
а) вес G стены, приложенный в ее центре тяжести, направленный по вертикали вниз и равный произведению объема стены на удельный вес кладки. Обозначим высоту, длину и ширину стены в метрах соответственно h,l и а. Удельный вес кладки 2 Г/см³, или, что то же, 2 Т/м³, следовательно,
G = 2hla Т;

б) давление P земляной насыпи, приложенное на 1/3 высоты стены, направленное горизонтально от насыпи к стенке и равное (в Т)
P =6l;

в) реакция R опоры. При решении подобных задач, называемых задачами на опрокидывание, нужно иметь в виду, что реакция связи бывает только в той опоре, вокруг которой опрокидывается тело, реакции же связей в опорах, в которых связь нарушится при опрокидывании тела, равны нулю.

Определив точку приложения реакции опоры, найдем направление реакции. Стена находится в равновесии под действием трех сил, а следовательно, линии действия всех трех сил должны пересекаться в одной точке, поэтому реакция опоры направлена под углом а к горизонтальной оси, причем

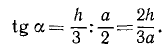
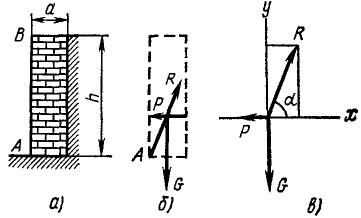
Рис. 19

Проецируя все приложенные к стене силы на горизонтальную и на вертикальную оси (рис. 19, в) и приравнивая нулю суммы проекций, найдем

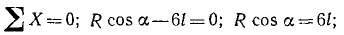
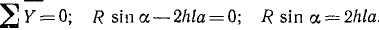
Легко находим, что наименьшая толщина стены a= 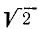м = 1,41 м. Чем толще стена, тем устойчивее ее равновесие. При значении а, меньшем найденного нами, силы не пересекутся в одной точке и равновесие невозможно, стена опрокинется.

В условии задачи использованы различные единицы измерений (тонна, грамм, метр, сантиметр). При решении мы выразили все величины в тоннах и метрах. Решим эту же задачу в СИ или MKC (м, кг, сек), для чего выразим в этих единицах все величины, заданные в условии задачи.

Давление земли на один метр длины стены
6 Т∕м = 6000 кГ/л = 6000 ^. 9,81 н/м.

Если длина стены I м, то давление на всю стену
P = 6000 ^. 9,81 ^. 1н.

Удельный вес кладки
2 Г∕cм³ = 2000 кГ/л» = 2000 ^. 9,81 н/м³.

Тогда вес стены
G = 2000 ^. 9,81 ^. hla н.

Составляя и решая уравнения равновесия всех сил, приложенных к стене, получим тот же ответ.
Ответ: a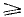 1,41 л.

Задача №4

На катеты равнобедренного прямоугольного треугольника АВС, сделанного из проволоки и установленного в вертикальной плоскости так, что гипотенуза AB горизонтальна (рис. 20, а), нанизаны два шарика: P весом G_l = 3 н и Q весом G₂ = 4 н, связанные нерастяжимой нитью. Найти положение равновесия (Угол 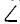CPQ = а), реакции катетов и натяжение нити, считая, что проволока Не прогибается и трение отсутствует.

Решение. Равновесие какого объекта надо рассмотреть, чтобы определить угол а натяжение нити T и две реакции катетов? Если рассматривать равновесие шарика Р, получим два уравнения равновесия (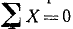 и 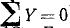) для трех неизвестных (угол а, натяжение T нити и реакция R_А катета АС). Если рассматривать равновесие шарика Q, то получим два других уравнения с тремя неизвестными (угол а, натяжение T нити и реакция Rb катета ВС), но две из этих неизвестных величин входят в уравнения равновесия шарика Р.

Для решения задачи надо: 1) рассмотреть равновесие шарика P и составить уравнения равновесия; 2) рассмотреть равновесие шарика Q и составить уравнения равновесия; 3) решить совместно все четыре уравнения и найти из них четыре неизвестных α, Т, R_А и R_В.

1)    Равновесие шарика P. На шарик P действуют силы: его вес 3 н, направленный вниз, натяжение T нити, направленное к Q, и реакция R_А катета АС.

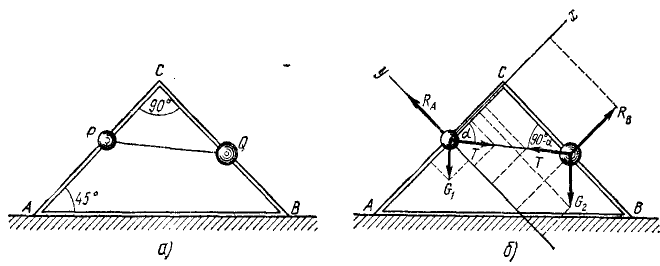
Рис. 20

Катет (проволока АС) осуществляет связь шарика Р. Эта связь допускает перемещение шарика лишь по АС. Реакция направлена перпендикулярно виртуальным перемещениям, т. е. перпендикулярно АС.
Построим систему координат с началом в центре шарика Р, направив ось Ox по катету к точке C (рис. 20, б).

Заметим, что мы вправе выбирать направления осей так, как это представляется целесообразным для упрощения выкладок. Мы свободны также в выборе начала координат.

Составляем уравнения равновесия системы сил, приложенных к шарику Р:

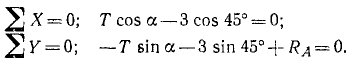
2)    Равновесие шарика Q. На шарик Q действуют вес 4 н, направленный вниз, сила T натяжения нити, направленная к шарику P (по принципу равенства действия и противодействия), и реакция R_В катета ВС, направленная перпендикулярно виртуальному перемещению шарика Q.

Нет необходимости строить новую систему координат, и мы можем проецировать силы, приложенные к шарику Q, на уже имеющиеся координатные оси. Получаем два новых уравнения:

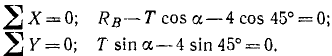
3)    Решая совместно четыре уравнения, находим четыре неизвестных.
Ответ.

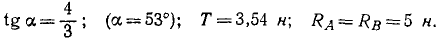
Задача №5

К шарниру кронштейна ABCD (рис. 21, а) приложена сила p= 6000 н. Кронштейн состоит из трех стержней АВ, AC и AD равной длины; крепления А, В, C и D шарнирные, плоскость ABC горизонтальна и BC=4D= =2 OD. Найти усилия в стержнях.

Решение. Рассматриваем равновесие точки А, в которой сходятся все неизвестные силы.

На точку А действует пространственный пучок сил: вес P = 6000 н, направленный вниз, усилия в стержнях АВ, AC и AD. Усилием в стержне называют силу, действующую вдоль стержня и растягивающую или сжимающую его; если стержень растянут, то на шарнир действует сила, направленная к стержню, если сжат, то от стержня. Не всегда бывает просто без предварительных расчетов определить, сжат данный стержень или растянут. Иногда этому помогает следующий прием: если от замены стержня нитью равновесие не нарушается, то стержень растянут, а если нарушается, то сжат. В данной задаче стержень AD, очевидно, можно заменить нитью, следовательно, он растянут и сила F_D, приложенная к шарниру А, направлена так, как тянула бы его нить, т. е. к D. Стержни AB и AC нитями заменить нельзя, так как кронштейн потеряет жесткость, следовательно, силы, приложенные к шарниру А, направлены от В и от С. Существует и другой способ, требующий предварительных расчетов: силы, действующие на шарнир со стороны стержней, при предварительном расчете считать растягивающими и всегда направлять от шарнира к стержням, составлять и решать уравнения равновесия, и если в результате решения этих уравнений для сил получаются положительные значения, то стержни растянуты, а если отрицательные, то сжаты. Этот способ мы применим в данной задаче и будем считать, что, кроме вертикальной нагрузки Р, на шарнир А действуют усилия в стержнях АВ, AC и AD, направленные условно от А к В, C и D.

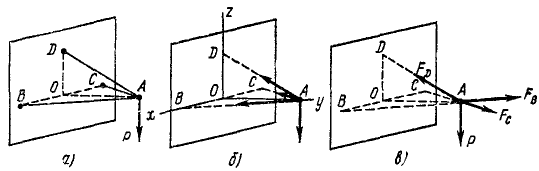
Рис. 21

Построим пространственную систему координат с началом в точке О (рис. 21,6), направив оси, как показано на чертеже. Из условия задачи следует, что ,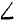ABO= ACO = 60°, 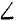OAB = 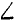OAD = 30°. Составляем уравнения равновесия пространственного пучка сил:

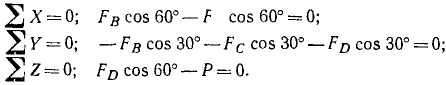
Решая эти уравнения, находим ответ.

Ответ. Стержень AB сжат, F_В=-6000 н; стержень AC сжат, F_c=—6000 н; стержень AD растянут, F_D=12000 н (рис. 21,в).

Для отличия сжимающую силу условимся писать (в некоторых задачах) c отрицательным знаком. Этот знак сжимающим силам приписывают условно.