
Волновые параметры длинной линии
Содержание:
Волновые параметры длинной линии:
Полученные в предыдущей лекции уравнения передачи длинной линии (23.8) описывают комплексные амплитуды напряжения 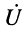
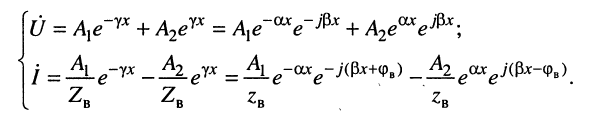
Тогда для мгновенных значений напряжений и токов в линии получаем:
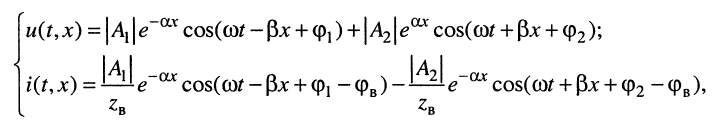 (24.1)
(24.1)
где 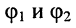 — аргументы комплексных величин
— аргументы комплексных величин 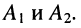
Решения (24.1) подтверждают, что напряжения и токи в длинной.линии являются функциями как времени 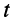 , так и координаты (расстояния)
, так и координаты (расстояния) 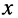 . Каждое из уравнений представляет собой сумму двух слагаемых, структуры которых тождественны, но отличаются только знаками перед коэффициентами затухания
. Каждое из уравнений представляет собой сумму двух слагаемых, структуры которых тождественны, но отличаются только знаками перед коэффициентами затухания 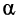 и фазы
и фазы 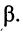 Сначала рассмотрим левые слагаемые уравнений (24.1)
Сначала рассмотрим левые слагаемые уравнений (24.1)
напряжений и токов, которые назовём падающими волнами напряжения и тока (смысл такого названия будет ясен из дальнейшего):
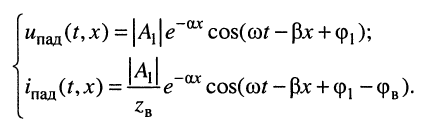 (24.2)
(24.2)
Из этих выражений следует:
- при любом фиксированном
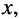 т. е. в любом сечении линии, и напряжение
т. е. в любом сечении линии, и напряжение 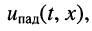 и ток
и ток 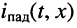 являются гармоническими колебаниями;
являются гармоническими колебаниями; - амплитуды колебаний убывают по мере удаления от начала к концу линии по экспоненциальному закону
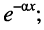
- в любом сечении линии отношение амплитуды напряжения
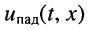 к амплитуде тока
к амплитуде тока 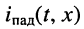 равно модулю волнового сопротивления
равно модулю волнового сопротивления 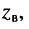 а разность фаз между ними равна аргументу
а разность фаз между ними равна аргументу 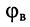 волнового сопротивления линии;
волнового сопротивления линии; - колебание напряжения
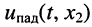 или тока
или тока 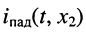 в сечении
в сечении 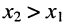 отстаёт по фазе от колебания и
отстаёт по фазе от колебания и 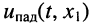 или
или 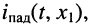 поскольку коэффициент фазы является величиной положительной:
поскольку коэффициент фазы является величиной положительной: 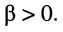
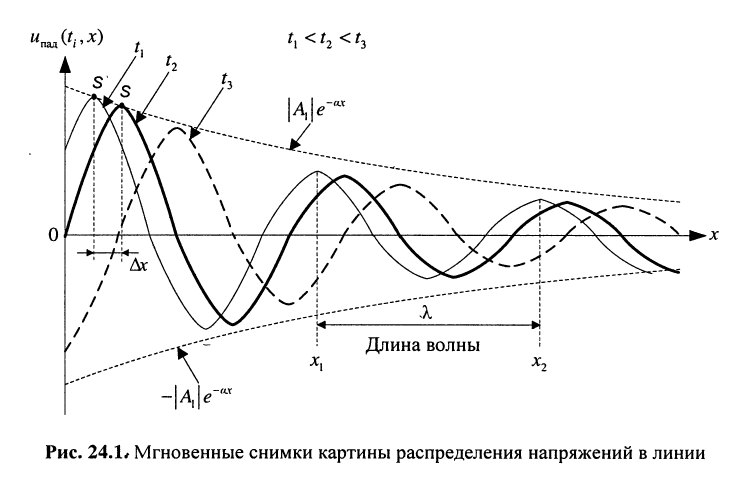
Сказанное демонстрируется на рис. 24.1, где представлено графическое распределение мгновенных значений напряжений 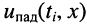 по линии для трёх последовательных моментов времени:
по линии для трёх последовательных моментов времени: 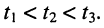 Эти графики можно рассматривать как последовательные мгновенные снимки картины распределения напряжений
Эти графики можно рассматривать как последовательные мгновенные снимки картины распределения напряжений 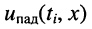 в указанные моменты времени. Они отображают волну, распространяющуюся от начала линии к концу. Например, рассматривая графики в моменты
в указанные моменты времени. Они отображают волну, распространяющуюся от начала линии к концу. Например, рассматривая графики в моменты 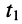 и
и 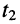 , замечаем, что в момент
, замечаем, что в момент 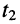 фаза напряжения в каждой точке линии изменится на величину
фаза напряжения в каждой точке линии изменится на величину 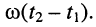 Огибающая процесса изображена пунктиром. Аналогичная картина имеет место и для тока.
Огибающая процесса изображена пунктиром. Аналогичная картина имеет место и для тока.
Определение:
Совокупность волн напряжения 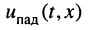 и тока
и тока 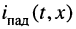 называется падающей волной.
называется падающей волной.
Найдём длину 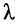 и скорость распространения падающей волны в линии.
и скорость распространения падающей волны в линии.
Под длиной волны понимают расстояние между смежными сечениями линии, фаза колебаний волны на которых отличается на 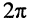 (рис. 24.1):
(рис. 24.1):
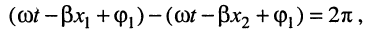
откуда имеем равенство
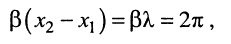
из которого получаем формулу для вычисления длины волны:
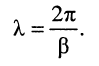 (24.3)
(24.3)
Определение:
Скоростью распространения, или фазовой скоростью, называют скорость 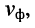 с которой распространяется в линии состояние равной фазы волны; например, скорость, с которой перемещается вдоль линии нуль напряжения или тока.
с которой распространяется в линии состояние равной фазы волны; например, скорость, с которой перемещается вдоль линии нуль напряжения или тока.
Нуль напряжения достигается в точках, где функция косинуса равна нулю, поэтому условие состояния равной фазы можно записать в виде равенства:
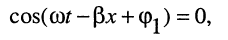
при этом аргумент имеет значения:
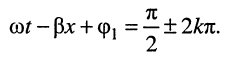
Продифференцировав обе части полученного равенства по переменной t, найдём скорость распространения нуля
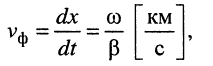 (24.4)
(24.4)
т. е. скорость распространения состояния равной фазы.
Фазовая скорость показывает, какое расстояние 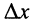 проходит точка
проходит точка 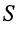 в единицу времени (см. рис. 24.1), и равна отношению частоты колебания к коэффициенту фазы.
в единицу времени (см. рис. 24.1), и равна отношению частоты колебания к коэффициенту фазы.
Рассмотрим, чему будет равен коэффициент фазы в наиболее характерной для практики области частот, когда 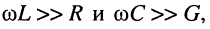 для чего разложим коэффициент распространения
для чего разложим коэффициент распространения 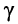 на вещественную и мнимую части:
на вещественную и мнимую части:
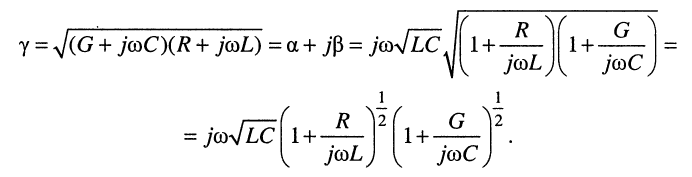
Разложение в ряды полученных в правой части биномиальных сомножителей и удержание в разложениях лишь по два слагаемых даёт:
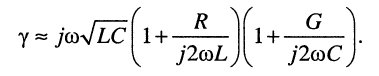
Раскрывая скобки и пренебрегая в произведении величиной второго порядка малости, получаем приближённое выражение для коэффициента распространения:
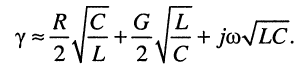 (24.5)
(24.5)
В линиях с хорошим диэлектриком проводимость чрезвычайно мала, поэтому второе вещественное слагаемое в выражении (24.5) оказывается очень малым по сравнению с первым, что позволяет записать формулы для коэффициентов затухания и фазы с хорошей степенью приближения:
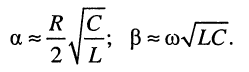 (24.6)
(24.6)
Тогда в указанной выше области частот фазовая скорость (24.4) согласно (24.6) оказывается равной
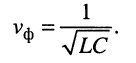
Подставляя сюда формулы значений первичных параметров длинной линии L и С (табл. 23.1), получаем:
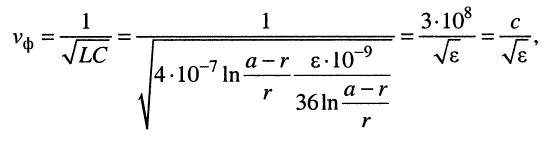 (24.7)
(24.7)
где с — скорость света.
Из (24.7) ясно, что для воздушных линий 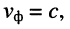 поскольку в этом случае можно считать
поскольку в этом случае можно считать 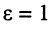 . Для коаксиального кабеля, у которого всегда
. Для коаксиального кабеля, у которого всегда 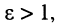 , фазовая скорость меньше скорости света в вакууме (например, при типовом значении
, фазовая скорость меньше скорости света в вакууме (например, при типовом значении 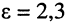 имеем
имеем 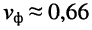 с).
с).
Интересно, что в области низких частот значение фазовой скорости убывает с уменьшением частоты. Это объясняется меньшим проявлением скин-эффекта: волна больше проникает в проводник, и колеблющиеся частицы внутри проводника возбуждают вторичные волны. Поскольку частицы обладают некоторой инерцией, образуемые ими вторичные волны запаздывают по фазе относительно вынуждающей колебания волны, поэтому происходит запаздывание фазы результирующей волны и, как следствие, уменьшение фазовой скорости.
Обратимся теперь ко вторым слагаемым уравнений (24.1), которые назовём отражёнными волнами напряжения и тока:
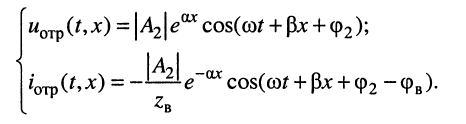 (24.8)
(24.8)
Проведя анализ этих слагаемых подобно тому, как это сделано для падающих волн, нетрудно убедиться, что они описывают затухающую волну такого же характера, как и падающая, но распространяющуюся в обратном направлении: от конца к началу линии.
Определение:
Волна напряжения 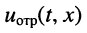 и тока
и тока 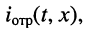 распространяющаяся от конца к началу линии, называется отражённой волной.
распространяющаяся от конца к началу линии, называется отражённой волной.
Соотношения между комплексными амплитудами падающих и отражённых волн
Из анализа, выполненного в разд. 24.1, следует:
- фазовая скорость отражённой волны совпадает с точностью до знака с фазовой скоростью падающей волны
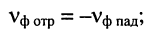
- амплитуда напряжения (тока) отражённой волны максимальна в конце амплитуда напряжения (тока) падающей волны минимальна в конце линии;
- напряжение
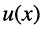 (ток) в любой точке длинной линии
(ток) в любой точке длинной линии 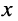 х является суммой напряжений (токов) падающей и отражённой волн:
х является суммой напряжений (токов) падающей и отражённой волн:
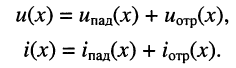
Переходя к комплексным амплитудам напряжений и токов падающей и отражённой волн, входящих в уравнения передачи длинной линии (23.8), последние суммы для любого сечения линии можно записать в виде:
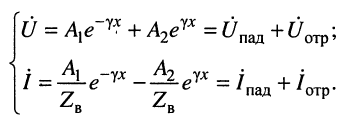 (24.9)
(24.9)
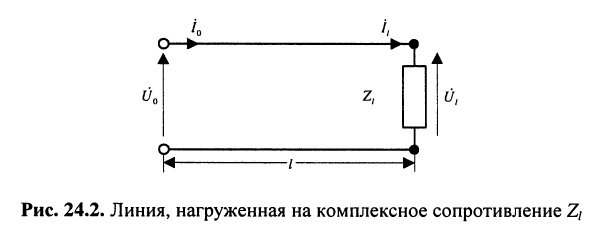
Практический интерес представляют соотношения между комплексными амплитудами падающих и отражённых волн в линии, имеющей длину 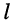 и нагруженной на комплексное сопротивление
и нагруженной на комплексное сопротивление 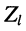 (рис. 24.2), когда на входе её действуют известные напряжение
(рис. 24.2), когда на входе её действуют известные напряжение 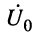 и ток
и ток 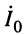 .
.
Волновое сопротивление
Прежде всего отметим, что при любом jc, т. е. в любой точке линии согласно (24.9) справедливы равенства:
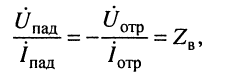 (24.10)
(24.10)
которое говорит о том, что в любом сечении линии .отношение комплексных амплитуд напряжения и тока падающей (отражённой) волны равно волновому сопротивлению линии 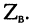
Свойства волнового сопротивления можно определить из выражений (24.10) и (23.6):
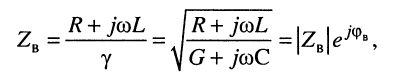
из которых следует:
модуль волнового сопротивления 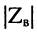 представляет собой отношение амплитуды напряжения к амплитуде тока падающей (отражённой) волны;
представляет собой отношение амплитуды напряжения к амплитуде тока падающей (отражённой) волны;
фаза (угол) 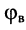 волнового сопротивления представляет собой разность между фазами напряжения и тока падающей (отражённой) волны;
волнового сопротивления представляет собой разность между фазами напряжения и тока падающей (отражённой) волны;
на частоте 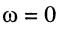 фаза
фаза 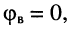 а само волновое сопротивление чисто активно
а само волновое сопротивление чисто активно
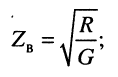
при стремлении частоты к бесконечности  фаза
фаза 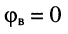 и волновое сопротивление как и в предыдущем случае чисто активно
и волновое сопротивление как и в предыдущем случае чисто активно
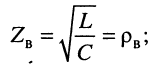
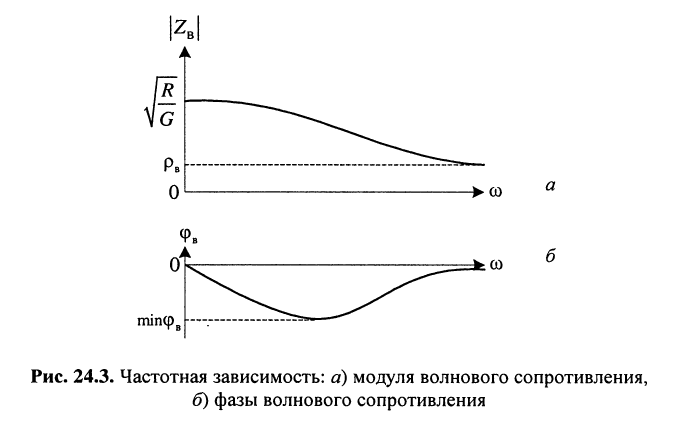
модуль волнового сопротивления 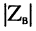 | с увеличением частоты уменьшается, поскольку для реальных линий
| с увеличением частоты уменьшается, поскольку для реальных линий 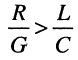 (рис. 24.3, а);
(рис. 24.3, а);
изменение фазы от нулевого значения при 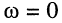 до нулевого значения при
до нулевого значения при говорит о том, что на одной из частот фаза будет минимальна (рис. 24.3, б), поскольку на всех частотах она является отрицательной.
говорит о том, что на одной из частот фаза будет минимальна (рис. 24.3, б), поскольку на всех частотах она является отрицательной.
Коэффициент отражения
Что касается соотношения между комплексными амплитудами напряжения (тока) падающей и отражённой волн, то оно оказывается различным в различных сечениях линии. Установить эти соотношения можно из системы (23.8), положив 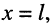 при условии, что напряжение
при условии, что напряжение 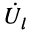 и ток
и ток 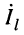 в конце линии известны. При этих условиях из (23.7) находятся два уравнения относительно комплексных амплитуд напряжения
в конце линии известны. При этих условиях из (23.7) находятся два уравнения относительно комплексных амплитуд напряжения 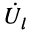 тока
тока 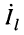 :
:
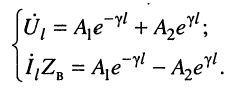 (24.11)
(24.11)
Из системы (24.11) согласно правилу Крамера получаем значения постоянных 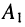 и
и 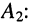
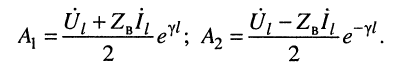
Подстановка найденных значений 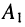 i и
i и 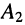 в (24.9) приводит к частному решению:
в (24.9) приводит к частному решению:
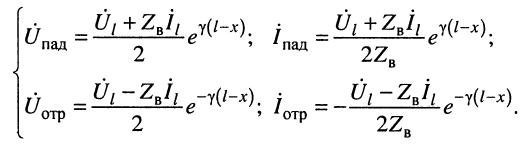 (24.12)
(24.12)
Система уравнений (24.12) позволяет записать отношение комплексных амплитуд напряжений и токов отражённой и падающей волн в сечении линии, расположенном на расстоянии 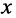 от её начала:
от её начала:
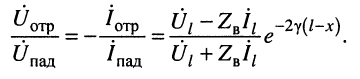 (24.13)
(24.13)
Но при выбранных направлениях отсчётов (рис. 24.2) напряжения 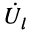 и тока
и тока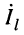 имеет место равенство
имеет место равенство 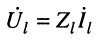 поэтому из (24.13) окончательно получаем:
поэтому из (24.13) окончательно получаем:
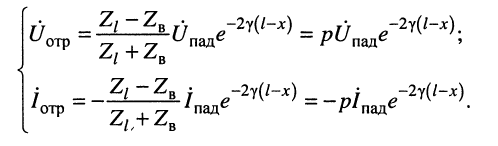 (24.14)
(24.14)
Определение:
Отношение
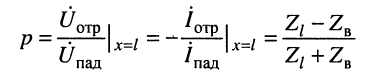 (24.15)
(24.15)
комплексной амплитуды напряжения отражённой волны к комплексной амплитуде напряжения падающей волны называется коэффициентом отражения.
Анализ соотношений (24.14) и (24.15) приводит к следующим выводам:
1. Коэффициент отражения является комплексной величиной и полностью зависит от волнового сопротивления линии 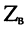 и сопротивления нагрузки
и сопротивления нагрузки 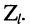 .
.
2. Коэффициент отражения по току отличается от коэффициента отражения по напряжению только знаком.
3. При 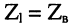 коэффициент отражения равен нулю р = 0, поэтому отражённая волна отсутствует. Линия, сопротивление нагрузки которой равно её волновому сопротивлению, называется нагруженной согласованно, а сопротивление нагрузки — согласованным сопротивлением. Любая другая нагрузка приводит к появлению в линии отражённой волны.
коэффициент отражения равен нулю р = 0, поэтому отражённая волна отсутствует. Линия, сопротивление нагрузки которой равно её волновому сопротивлению, называется нагруженной согласованно, а сопротивление нагрузки — согласованным сопротивлением. Любая другая нагрузка приводит к появлению в линии отражённой волны.
4. Отношение амплитуд отражённой и падающей волн (см. (24.14) и (24.15))
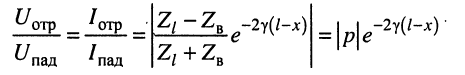
убывает с удалением от конца линии к её началу
5. В режиме короткого замыкания, когда 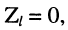 коэффициент отражения по напряжению р = -1, а коэффициент отражения по току
коэффициент отражения по напряжению р = -1, а коэффициент отражения по току
р = 1. Это означает, что напряжения отражённой и падающей волн в конце линии находятся в противофазе:
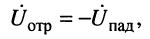
а результирующее напряжение равно нулю
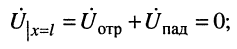
при этом токи падающей и отражённой волн оказываются в фазе
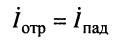
и результирующий ток равен удвоенному току падающей волны
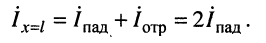
6. В режиме холостого хода, когда 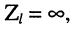 коэффициент отражения по напряжению р = 1, поэтому имеет место ситуация, противоположная относительно вывода, указанного в п. 5: напряжения отражённой и падающей волн в конце линии находятся в фазе:
коэффициент отражения по напряжению р = 1, поэтому имеет место ситуация, противоположная относительно вывода, указанного в п. 5: напряжения отражённой и падающей волн в конце линии находятся в фазе:
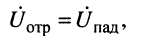
и результирующее напряжение равно удвоенному напряжению падающей волны
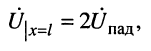
а ток равен нулю
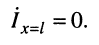
Уравнения передачи согласованно нагруженной длинной линии
Ранее (см. разд. 23.3) были получены уравнения передачи длинной линии (23.8), которые представляют собой общее решение телеграфных уравнений и описывают закон распределения напряжений и токов по всей линии. Для решения же большинства практических задач достаточно знать соотношения лишь между напряжениями и токами на внешних зажимах линии и вовсе не интересоваться законом распределения напряжений и токов по длине линии. Иначе говоря, на практике вполне достаточно рассматривать линию как согласованно нагруженный четырёхполюсник, полностью описываемый соответствующими уравнениями передачи.
Поставим задачу найти уравнения передачи согласованно нагруженной линии, которые связывают комплексные амплитуды напряжений и токов на её внешних зажимах.
Воспользуемся уравнениями (24.12) для комплексных амплитуд напряжений и токов падающей и отражённой волн и подставим их в систему (24.9):
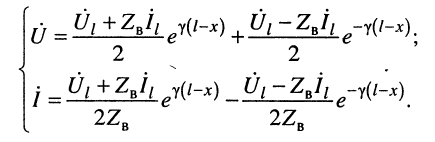 (24.16)
(24.16)
Если в систему (24.9) подставить выражения (24.14), получим
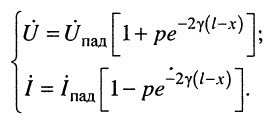 (24.17)
(24.17)
Системы (24.16) и (24.17) представляют собой системы уравнений передачи длинной линии. Обычно комплексные амплитуды напряжения и тока на входных зажимах линии (х = 0) обозначают через 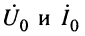 (см. рис. 24.2); при таких обозначениях из системы (24.16) получаем наиболее удобную форму записи уравнений передачи линии:
(см. рис. 24.2); при таких обозначениях из системы (24.16) получаем наиболее удобную форму записи уравнений передачи линии:
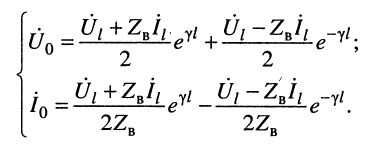 (24.18)
(24.18)
В большинстве случаев уравнения (24.8) записывают в более компактном виде:
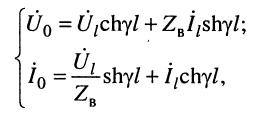 (24.19)
(24.19)
где
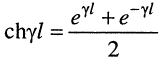 — гиперболический косинус
— гиперболический косинус
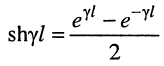 — гиперболический синус.
— гиперболический синус.
Для режима согласованной нагрузки, когда 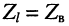 и
и 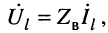 т. е. когда отсутствует отражённая волна, из (24.18) получаем уравнения передачи согласованно нагруженной линии:
т. е. когда отсутствует отражённая волна, из (24.18) получаем уравнения передачи согласованно нагруженной линии:
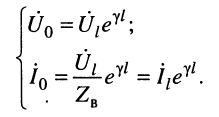 (24.20)
(24.20)
Именно в такой режим и стремятся поставить линию связи, поскольку отражённые волны вызывают ряд нежелательных явлений, о чём речь пойдёт далее.
Постоянная передачи и частотные характеристики длинной линии
Постоянная передачи длинной линии:
Определение
Безразмерная комплексная величина, равная произведению коэффициента распространения 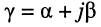 на длину линии
на длину линии 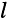
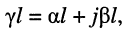 (24.21)
(24.21)
называется постоянной передачи линии.
Вещественная часть постоянной передачи 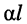 называется собственным, волновым или характеристическим затуханием линии, а мнимая часть
называется собственным, волновым или характеристическим затуханием линии, а мнимая часть 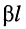 — собственной, волновой или характеристической фазой.
— собственной, волновой или характеристической фазой.
Постоянная передачи и входящие в неё параметры характеризуют линию как таковую и не зависят от свойств генератора и нагрузки, между которыми линия может быть включена.
Поскольку режим согласованной нагрузки для линии является типовым, найдём указанные ранее параметры только для этого режима.
В таком случае постоянную передачи можно получить, прологарифмировав уравнения (24.20):
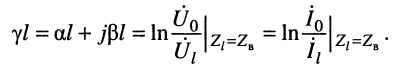 (24.22)
(24.22)
Подставляя отношения комплексных амплитуд
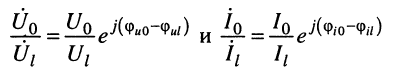
под знак логарифма, получаем:
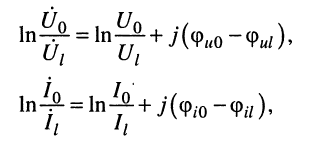
на основании чего можно записать два равноправных выражения для коэффициента распространения
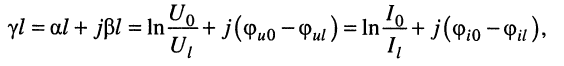
откуда имеем:
собственное затухание линии
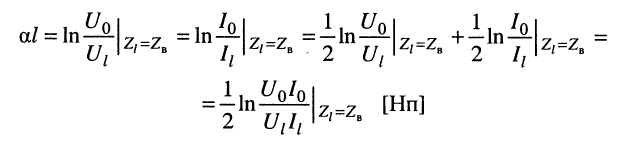 (24.3)
(24.3)
и её собственную фазу
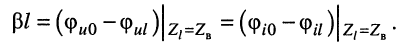 (24.24)
(24.24)
Из выражений (24.23) и (24.24) следует, что для согласованно нагруженной линии:
собственное затухание линии 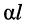 [Нп] равно натуральному логарифму отношения амплитуд или действующих значений напряжений (токов) на входе и выходе; оно равно также половине натурального логарифма отношения полных мощностей на входе и выходе;
[Нп] равно натуральному логарифму отношения амплитуд или действующих значений напряжений (токов) на входе и выходе; оно равно также половине натурального логарифма отношения полных мощностей на входе и выходе;
собственная фаза линии равна разности начальных фаз колебаний напряжений (токов) на входе и выходе.
Собственное затухание линии часто оценивается в децибелах:
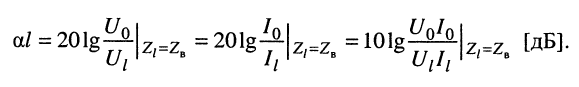 (24.25)
(24.25)
В этом случае нетрудно переформулировать зависимость собственного затухания, выраженного в децибелах, через десятичные логарифмы отношений амплитуд напряжений (токов) или полных мощностей.
Пример 24.1.
Оценим потери мощности телевизионного сигнала при распространении его в фидере' от системы антенн до усилителя головной станции и в коаксиальном кабеле сети кабельного телевидения на отрезках магистральной линии между магистральными усилителями (рис. 24.4).
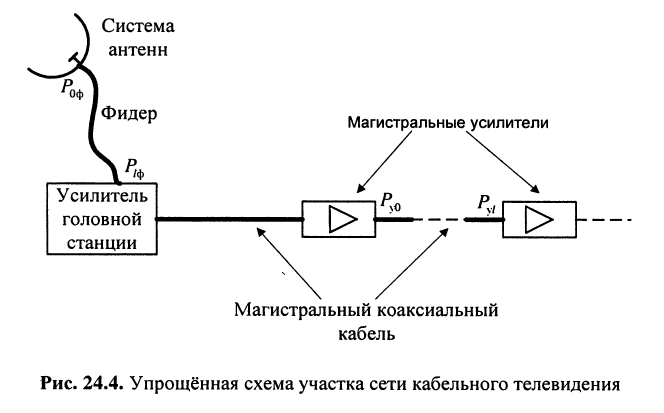
Решение. Затухание фидера зависит от его конструкции, длины 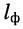 и коэффициента затухания
и коэффициента затухания 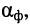 который измеряется на средней частоте частотного диапазона фидера. Обычный фидерный тракт имеет длину 50—150 м. Типовым кабелем, используемом при конструировании фидерных трактов, является кабель РК-75-24-51, имеющий полосу пропускания 50—600 МГц и коэффициент затухания
который измеряется на средней частоте частотного диапазона фидера. Обычный фидерный тракт имеет длину 50—150 м. Типовым кабелем, используемом при конструировании фидерных трактов, является кабель РК-75-24-51, имеющий полосу пропускания 50—600 МГц и коэффициент затухания 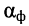 = 0,002 дБ/м на частоте 300 МГц. Тогда при средней длине фидера
= 0,002 дБ/м на частоте 300 МГц. Тогда при средней длине фидера 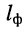 = 100 его собственное затухание (24.25) оказывается равным
= 100 его собственное затухание (24.25) оказывается равным
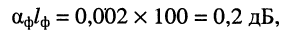
а отношение мощности сигнала на выходе фидера 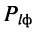 к мощности сигнала на входе фидера
к мощности сигнала на входе фидера 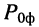 составляет
составляет
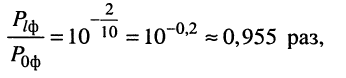
т. е. потери мощности в фидере невелики.
Фидер — линия для передачи электрических колебаний высокой частоты от радиопередатчика к антенне и от антенны к радиоприёмнику.
В то же время типовой магистральный коаксиальный кабель QR 540 JCA имеет полосу пропускания 5—1000 МГц и коэффициент затухания 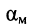 = 0,0354 дБ/м на частоте 300 МГц.
= 0,0354 дБ/м на частоте 300 МГц.
Расстояние 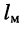 между смежными усилителями магистрали обычно составляет до
между смежными усилителями магистрали обычно составляет до 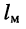 = 2 км. Следовательно, собственное затухание отрезка магистрального кабеля равно
= 2 км. Следовательно, собственное затухание отрезка магистрального кабеля равно
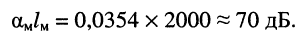
Последнее означает, что полная мощность на входе последующего усилителя 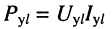 меньше полной мощности
меньше полной мощности 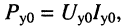 которая отдаётся в линию предшествующим усилителем, в десятки миллионов раз, поскольку согласно (24.25)
которая отдаётся в линию предшествующим усилителем, в десятки миллионов раз, поскольку согласно (24.25)
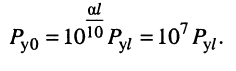
Частотные характеристики (АЧХ и ФЧХ) согласованно нагруженной длинной линии
Исходя из уравнений передачи согласованно нагруженной линии (24.20) запишем её комплексную частотную характеристику через постоянную передачи линии:
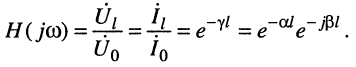 (24.26)
(24.26)
Отсюда нетрудно получить постоянную передачи через КЧХ линии:
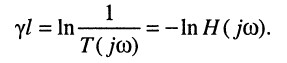 (24.27)
(24.27)
Амплитудно-частотная и фазочастотная характеристики определяются из (24.26):
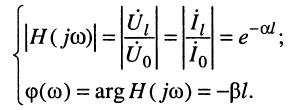 (24.28)
(24.28)
Для несогласованной нагруженной линии КЧХ можно найти из её уравнений передачи (24.18), подставив в них равенства:
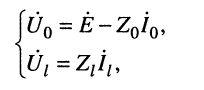
где 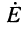 и
и 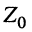 — комплексная амплитуда ЭДС и комплексное внутреннее сопротивление генератора, подключённого к линии.
— комплексная амплитуда ЭДС и комплексное внутреннее сопротивление генератора, подключённого к линии.
Входное сопротивление длинной линии
Определение:
Входным сопротивлением линии 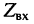 называется отношение комплексной амплитуды напряжения
называется отношение комплексной амплитуды напряжения 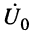 к комплексной амплитуде тока
к комплексной амплитуде тока 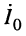 , действующих на входе линии.
, действующих на входе линии.
Формулу входного сопротивления для линии с произвольной нагрузкой можно получить из уравнений (24.17), если положить расстояние 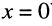 и разделить первое уравнение на второе:
и разделить первое уравнение на второе:
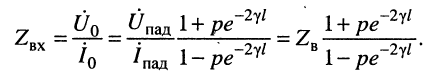 (24'29)
(24'29)
Анализ формулы (24.29) показывает:
при согласованной нагрузке входное сопротивление равно волновому, поскольку в данном случае 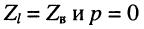 (24.15);
(24.15);
если постоянная передачи линии стремится к бесконечности 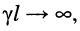 то входное и волновое сопротивления весьма близки по величине
то входное и волновое сопротивления весьма близки по величине 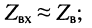 считают, что
считают, что 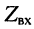 не зависит от нагрузки при собственном затухании линии
не зависит от нагрузки при собственном затухании линии 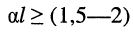 Нп;
Нп;
в режиме КЗ 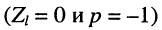 получаем
получаем
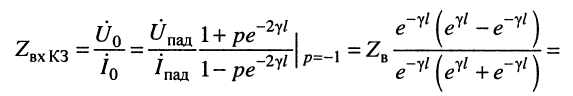 (24.30)
(24.30)
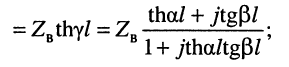
в режиме XX 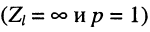 имеем
имеем
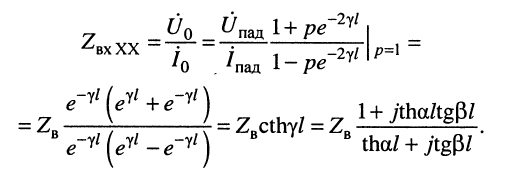 (24.31)
(24.31)
Вывод:
волновое сопротивление линии представляет собой предел, к которому стремится входное сопротивление при безграничном увеличении длины линии:
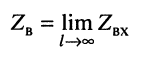
Этот факт объясняется тем, что при большом затухании линии значительная часть мощности, подводимой к её входу, рассеивается в самой линии и лишь небольшой остаток мощности поступает в нагрузку (см. пример 24.1). По этой причине энергетические соотношения на входе линии пренебрежимо мало зависят от энергетических соотношений на её выходе и, в частности, от сопротивления нагрузки линии.
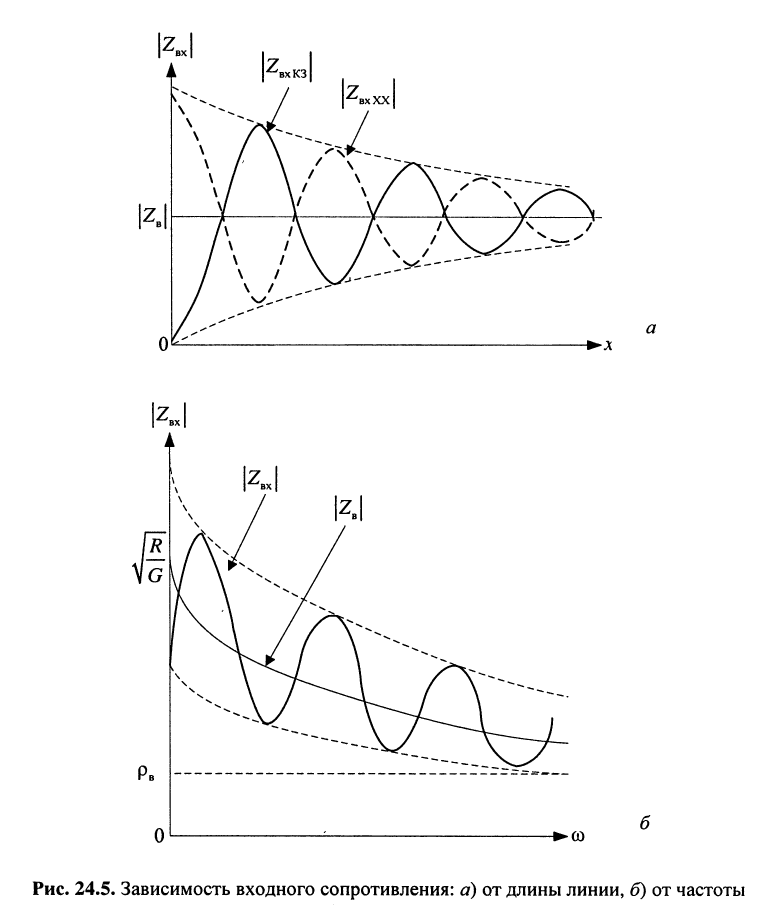
С увеличением длины линии увеличивается и её затухание, а потому уменьшается амплитуда отражённой волны на входе линии, что, в свою очередь, приводит к уменьшению отклонения входного сопротивления линии от её волнового сопротивления как по модулю, так и по фазе. В пределе входное сопротивление линии стремится к волновому сопротивлению. На рис. 24.5, а показаны зависимости модулей входных сопротивлений в режимах XX и КЗ. Колебательный характер волнового сопротивления при несогласованной нагрузке объясняется наличием падающих и отражённых волн.
Входное сопротивление зависит не только от длины линии, но и от частоты (рис. 24.5, б). С ростом частоты увеличиваются как собственное затухание 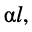 так и собственная фаза
так и собственная фаза 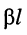 линии. Это приводит к весьма сложному волнообразному характеру изменения входного сопротивления линии относительно её волнового сопротивления.
линии. Это приводит к весьма сложному волнообразному характеру изменения входного сопротивления линии относительно её волнового сопротивления.
Допустимые отклонения входного сопротивления линии от её волнового сопротивления строго нормированы, и при эксплуатации длинных линий необходимо придерживаться указываемых для линии обычно весьма жёстких норм.
Определение параметров линии методом холостого хода и короткого замыкания
Определение первичных и вторичных параметров линии наиболее просто осуществлять с помощью измерений входного сопротивления линии при двух граничных сопротивлениях нагрузки: холостом ходе и коротком замыкании.
Из уравнений (24.19) в режимах 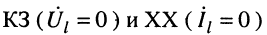 имеем
имеем
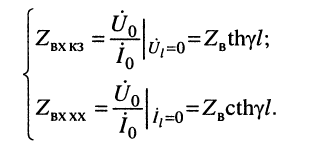
Совместное решение этих уравнений позволяет найти значения волновых параметров линии: волнового сопротивления и постоянной передачи.
Волновое сопротивление
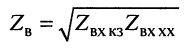 (24.32)
(24.32)
равно среднему геометрическому из входных сопротивлений короткозамкнутой и разомкнутой линии. Это выражение можно рассматривать как ещё одно определение волнового сопротивления длинной линии.
Гиперболический тангенс постоянной передачи 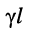
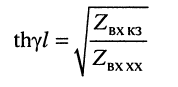 (24.33)
(24.33)
равен среднему геометрическому из сопротивления 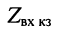 короткозамкнутой линии и проводимости
короткозамкнутой линии и проводимости 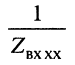 — разомкнутой линии. Найдём из (24.33) постоянную передачи
— разомкнутой линии. Найдём из (24.33) постоянную передачи 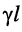 и коэффициент распространения
и коэффициент распространения 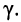 Поскольку
Поскольку
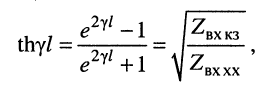
то
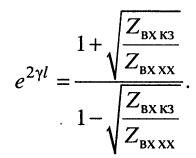
Логарифмируя обе части последнего равенства, получаем постоянную передачи:
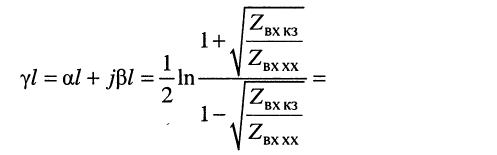
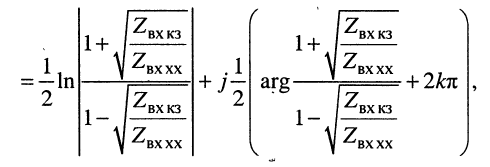 (24.34)
(24.34)
откуда легко находятся коэффициенты затухания и фазы:
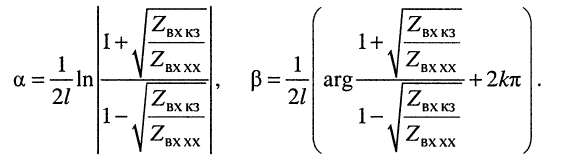
Коэффициент 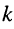 равен целому числу волн, укладывающихся по длине линии.
равен целому числу волн, укладывающихся по длине линии.
Во всех формулах необходимо брать только арифметические корни.
Зная волновые параметры линии, нетрудно вычислить её первичные параметры путём приравнивания вещественных и мнимых частей равенств:
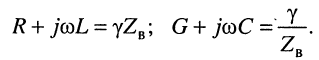
Замечание:
Метод холостого хода и короткого замыкания целесообразно применять в том случае, когда затухание линии не превышает
1 Нп (8,69 дБ), что характерно для большинства длинных линий.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |