
Формулы двойного аргумента с примерами решения
Содержание:
Преобразования тригонометрических выражений можно упростить, если рассмотреть частные случаи общих формул. Рассмотрим формулу синуса суммы 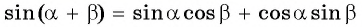
Формула синуса двойного аргумента
Получили формулу синуса двойного аргумента: 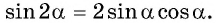
Выведем формулу косинуса двойного аргумента. Используем формулу косинуса суммы 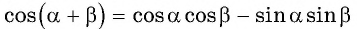 для случая
для случая 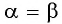 и получим:
и получим:
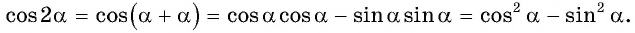
Формула косинуса двойного аргумента
Формула косинуса двойного аргумента: 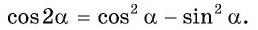
Для вывода формулы тангенса двойного аргумента рассмотрим формулу тангенса суммы 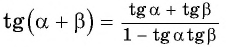 при
при 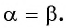 В этом случае имеем:
В этом случае имеем: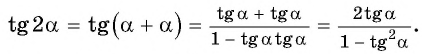
Формула тангенса двойного аргумента
Получили формулу тангенса двойного аргумента: 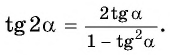

Пример №1
Упростите выражение:
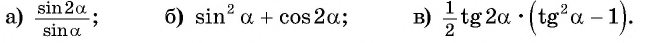
Решение:
Применим формулы двойного аргумента:
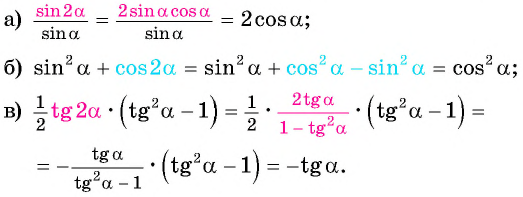
Пример №2
Вычислите:
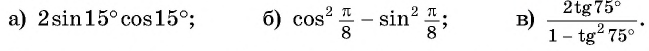
Решение:
Применим формулы двойного аргумента «справа налево»:
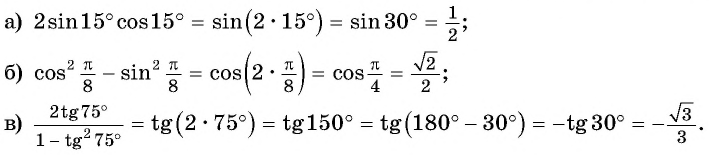
Пример №3
Найдите значение выражения 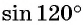 двумя способами.
двумя способами.
Решение:
Первый способ. Применим формулы приведения:
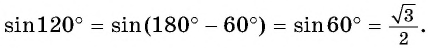
Второй способ. Применим формулу синуса двойного аргумента:
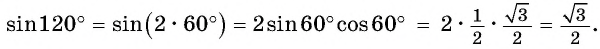
Пример №4
Представьте данный угол в виде 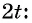

Решение:
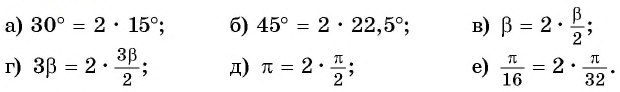
Пример №5
Преобразуйте каждое из выражений с помощью формул двойного угла: 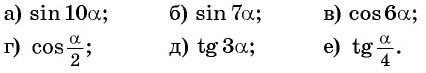
Решение:
Представим угол в каждом из выражений в виде 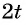 и применим формулу двойного аргумента:
и применим формулу двойного аргумента:
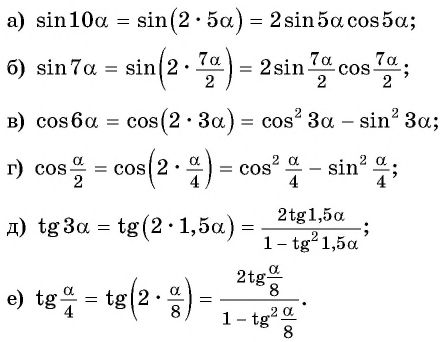
Пример №6
Упростите выражение:
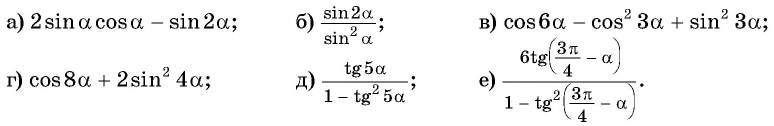
Решение:
Применим формулы двойного аргумента и получим:
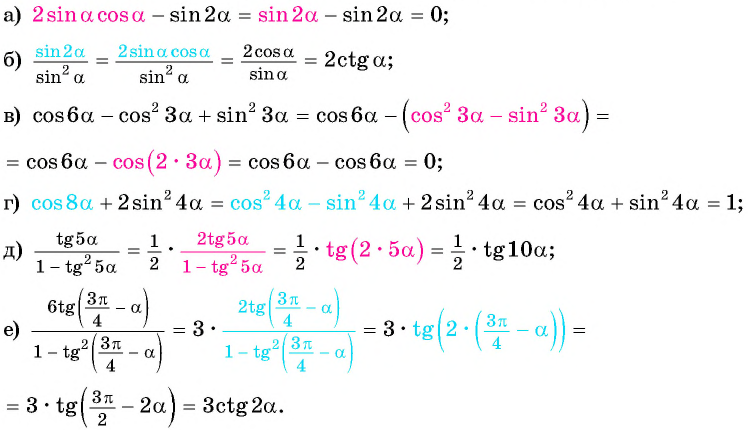
Пример №7
Найдите значение выражения:

Решение:
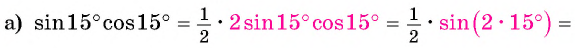
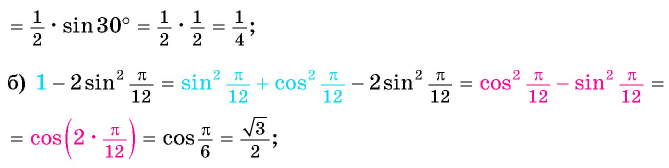
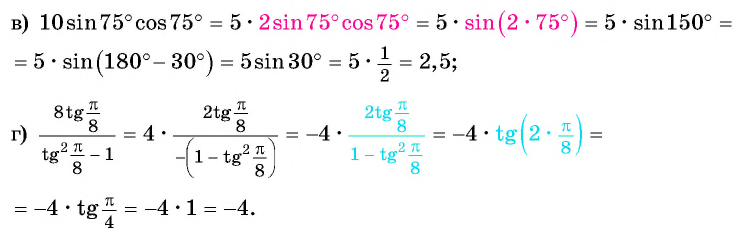
Пример №8
Вычислите 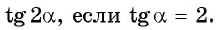
Решение:
Применим формулу тангенса двойного аргумента и получим: 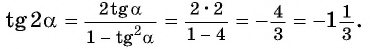
Пример №9
Вычислите:
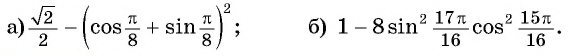
Решение:
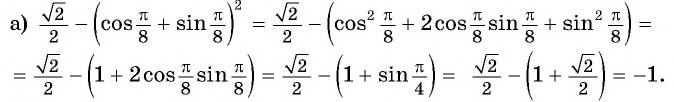
б) По формулам приведения
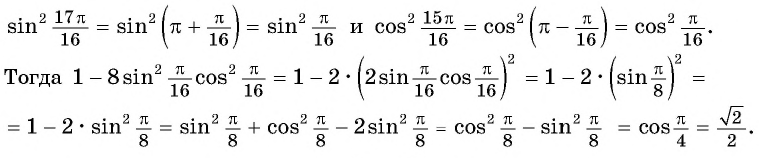
Пример №10
Вычислите 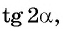 если
если 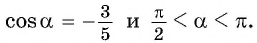
Решение:
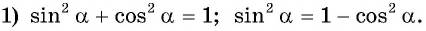 Так как
Так как 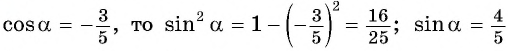 или
или 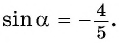 Поскольку
Поскольку 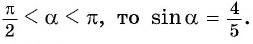
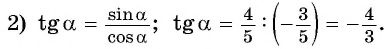
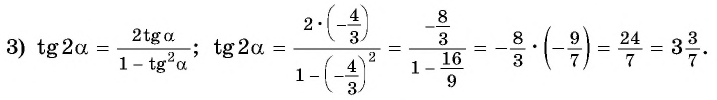
Ответ: 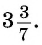
Пример №11
Решите уравнение 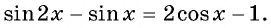
Решение:
Используем формулу синуса двойного аргумента:
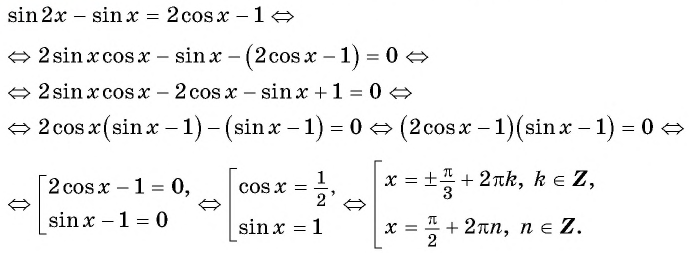 Ответ:
Ответ: 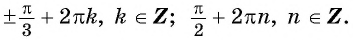
Пример №12
Решите уравнение 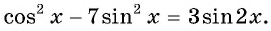
Решение:
Воспользуемся формулой синуса двойного угла и получим 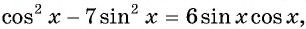 или
или 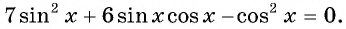 Так как значения переменной, при которых
Так как значения переменной, при которых 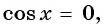 не являются корнями данного уравнения, то разделим обе части уравнения на
не являются корнями данного уравнения, то разделим обе части уравнения на 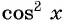 и получим
и получим 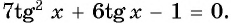
Пусть 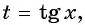 тогда уравнение примет вид
тогда уравнение примет вид 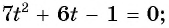
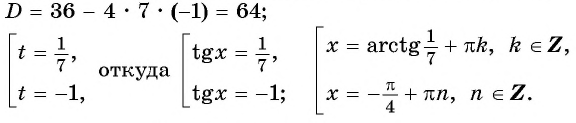 Ответ:
Ответ: 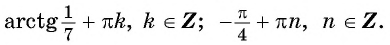
Пример №13
Докажите тождество 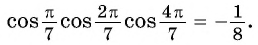
Решение:
Умножим и разделим выражение 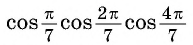 на
на 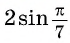 и применим формулу синуса двойного аргумента:
и применим формулу синуса двойного аргумента:
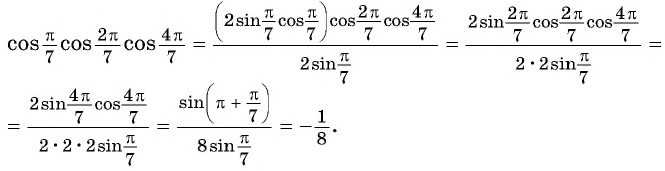
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Формулы преобразования суммы и разности синусов (косинусов) в произведение
- Корень n-й степени из числа и его свойства
- Свойства и график функции y=ⁿ√x (n>1, n∈N)
- Иррациональные уравнения
- Тригонометрические уравнения
- Тригонометрические неравенства
- Формулы приведения
- Синус, косинус, тангенс суммы и разности