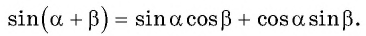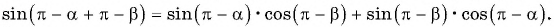Синус, косинус, тангенс суммы и разности с примерами решения
Содержание:
Известные значения синуса, косинуса, тангенса углов можно использовать для вычисления значений синуса, косинуса, тангенса других углов.
Угол 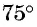
Выведем формулу 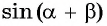 — синуса суммы двух углов. Рассмотрим случай, когда
— синуса суммы двух углов. Рассмотрим случай, когда 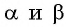 — острые углы в треугольнике
— острые углы в треугольнике 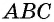 (рис. 115).
(рис. 115). 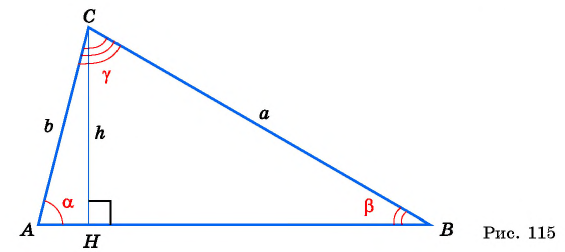
Выразим площадь треугольника 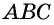 дважды:
дважды:
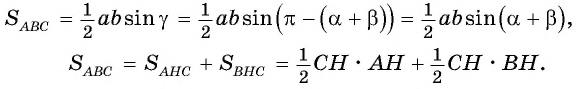
Треугольник 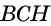 — прямоугольный, тогда
— прямоугольный, тогда 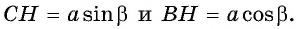 Из прямоугольного треугольника
Из прямоугольного треугольника 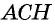 имеем:
имеем: 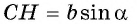 и
и 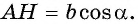 Тогда
Тогда
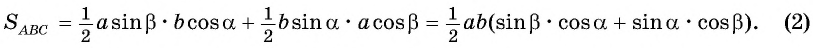
Приравняем правые части равенств (1) и (2):
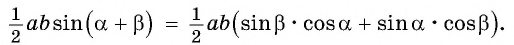
Разделим обе части равенства на 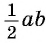 и получим формулу синуса суммы двух углов:
и получим формулу синуса суммы двух углов:
Если углы 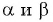 не являются острыми, то можно воспользоваться свойством периодичности синуса и формулами приведения.
не являются острыми, то можно воспользоваться свойством периодичности синуса и формулами приведения.
Например, если 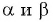 являются углами второй четверти, то
являются углами второй четверти, то 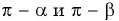 — острые углы.
— острые углы.
Применим к ним выведенную для острых углов формулу синуса суммы:
Воспользуемся формулами приведения в левой части равенства (3) и получим: 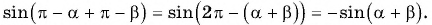
Применим формулы приведения к правой части равенства (3): 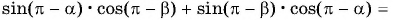
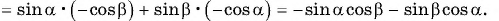
Таким образом,
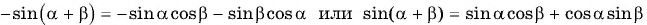 — формула синуса суммы двух углов.
— формула синуса суммы двух углов.
Остальные случаи принадлежности углов различным четвертям рассматриваются аналогично предыдущему.
Синус суммы
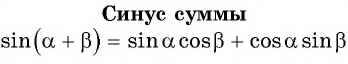
Воспользуемся полученной формулой 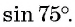
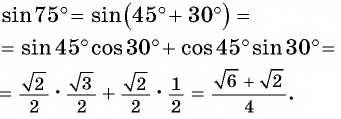
Выведем формулу синуса разности двух углов.
Для этого 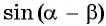 представим в виде
представим в виде 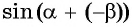 и применим формулу синуса суммы двух углов:
и применим формулу синуса суммы двух углов:
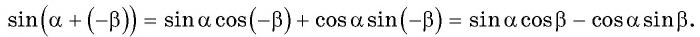
Получили формулу синуса разности двух углов:
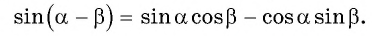
Синус разности
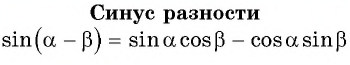
Вычислим, например, 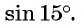
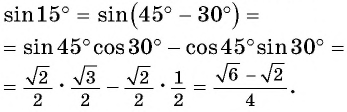
Для вывода формулы косинуса суммы двух углов воспользуемся формулами приведения и получим: 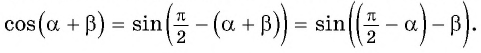
Тогда по формуле синуса разности двух углов имеем:
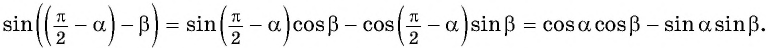
Получили формулу косинуса суммы двух углов:
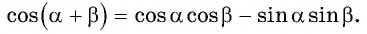
Косинус суммы

Применим полученную формулу и вычислим, например, 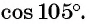
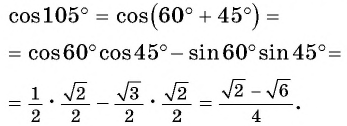
Представив разность  в виде суммы
в виде суммы 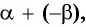 можно получить формулу косинуса разности двух углов:
можно получить формулу косинуса разности двух углов: 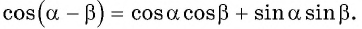
Косинус разности
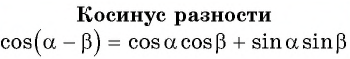 Найдем, например,
Найдем, например, 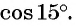
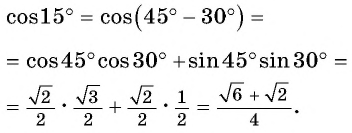
Пример №1
Вычислите:
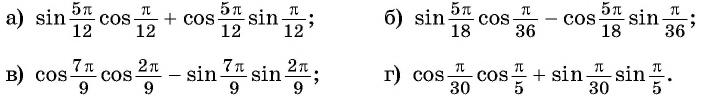
Решение:
Применим полученные формулы «справа налево»: 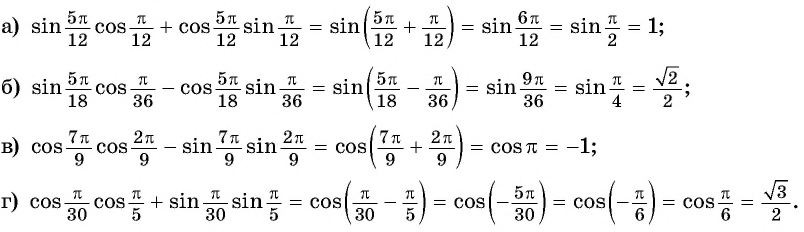 Выведем формулы тангенса суммы и тангенса разности двух углов.
Выведем формулы тангенса суммы и тангенса разности двух углов.
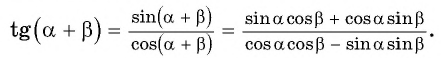 Разделим числитель и знаменатель дроби на
Разделим числитель и знаменатель дроби на 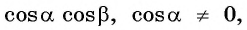
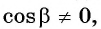 тогда:
тогда:
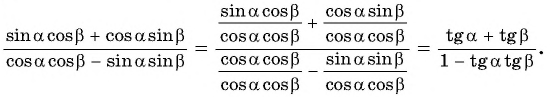
Таким образом, получили формулу тангенса суммы двух углов:
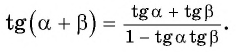
Воспользуемся формулой тангенса суммы и вычислим, например, 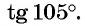
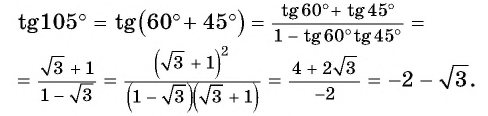
Тангенс суммы
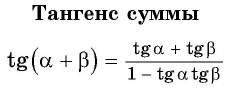 Представив разность
Представив разность 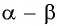 в виде суммы
в виде суммы 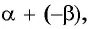 можно получить формулу тангенса разности двух углов:
можно получить формулу тангенса разности двух углов:
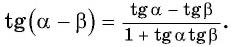 Найдем, например,
Найдем, например, 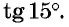
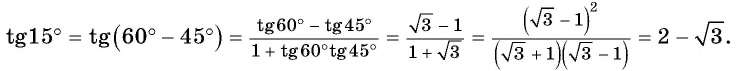
Тангенс разности
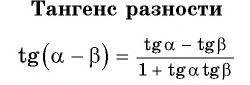
Пример №2
Вычислите:
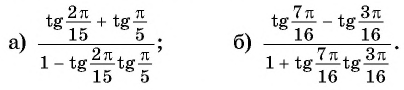
Решение:
Применим формулы тангенса суммы и тангенса разности «справа налево»:
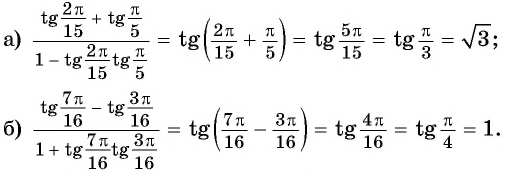
Полученные формулы синуса суммы, синуса разности, косинуса суммы, косинуса разности, тангенса суммы, тангенса разности двух углов называют формулами сложения.
Примеры заданий и их решения
Пример №3
С помощью формул сложения преобразуйте выражение:

Решение:
а) По формуле синуса разности получим:
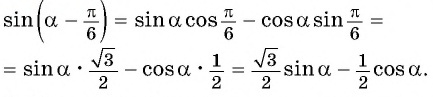
б) Применим формулу тангенса суммы:
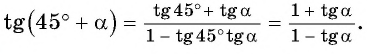
Пример №4
Найдите значение выражения:
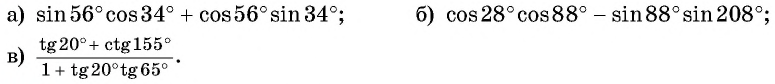
Решение:
а) По формуле синуса суммы получим:
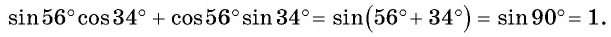
б) По формулам приведения получим, что 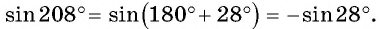
Тогда 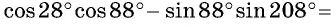
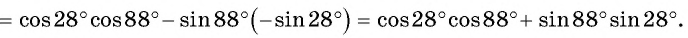 Воспользуемся формулой косинуса разности и получим:
Воспользуемся формулой косинуса разности и получим:
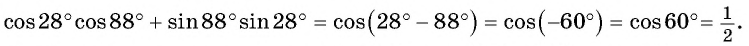
в) По формулам приведения 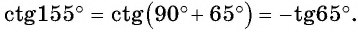
Тогда 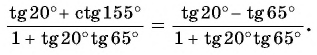
По формуле тангенса разности:
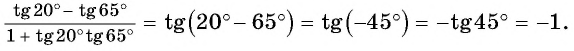
Пример №5
Вычислите:

Решение:
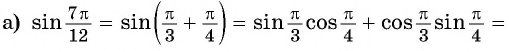
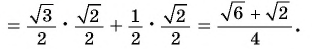
б) По формулам приведения: 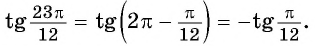
По формуле тангенса разности получим:
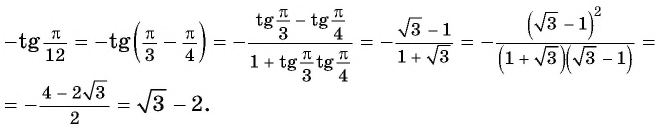
Таким образом, 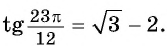
Пример №6
Упростите выражение:
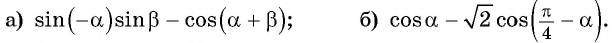
Решение:
а) Воспользуемся нечетностью синуса и формулой косинуса разности:
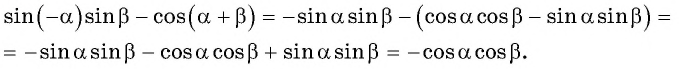
б) Применим формулу косинуса разности и получим: 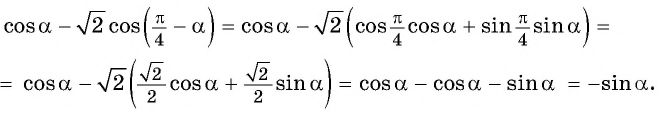
Пример №7
Решите уравнение 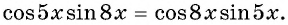
Решение:
Запишем уравнение в виде 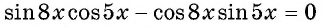 и по формуле синуса разности получим:
и по формуле синуса разности получим: 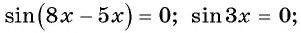
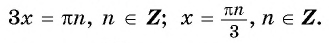
Ответ: 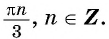
Пример №8
Вычислите 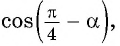 если
если 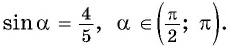
Решение:
Применим формулу косинуса разности:
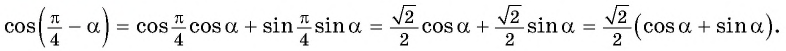
Из основного тригонометрического тождества выразим 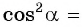
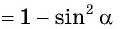 и найдем
и найдем 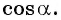 Так как
Так как 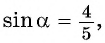 то
то 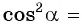
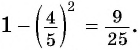 Значит,
Значит, 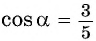 или
или 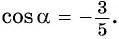 Поскольку
Поскольку 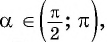 т. е.
т. е. 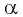 угол второй четверти, то
угол второй четверти, то 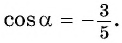 Тогда
Тогда
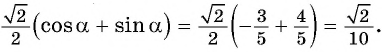
Пример №9
Докажите тождество 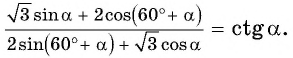
Решение:
Воспользуемся формулами сложения и получим:
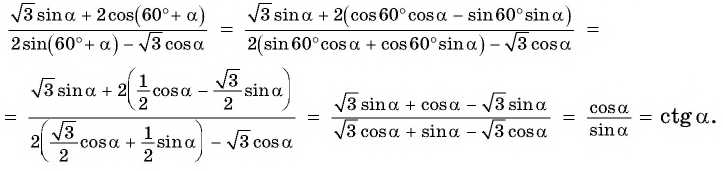
Пример №10
Найдите значение выражения:
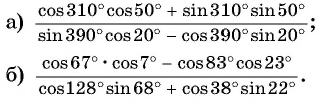
Решение:
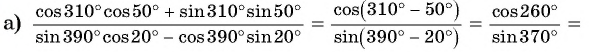
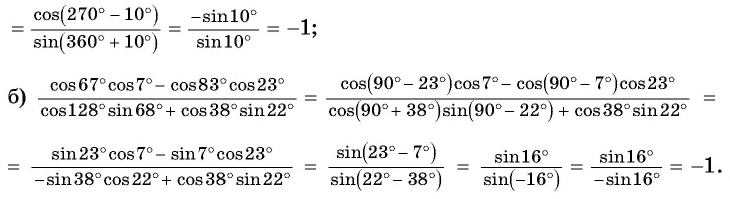 9.
9.
Пример №11
Найдите множество значений функции
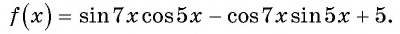
Решение:
Применим формулу синуса разности и запишем функцию в виде 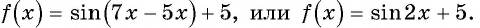
Так как 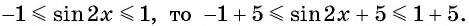 Таким образом, имеем:
Таким образом, имеем: 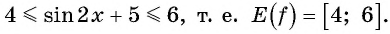
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Формулы двойного аргумента
- Формулы преобразования суммы и разности синусов (косинусов) в произведение
- Корень n-й степени из числа и его свойства
- Свойства и график функции y=ⁿ√x (n>1, n∈N)
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Тригонометрические неравенства
- Формулы приведения