
Корень n-й степени с примерами решения
Содержание:
Перейдем к изучению корней степени п для произвольного натурального числа 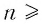
Определение:
Пусть 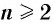
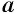 называется такое число
называется такое число 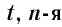 степень которого равна
степень которого равна 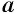 .
.
Таким образом, утверждение «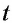 — корень
— корень 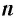 -й степени из
-й степени из 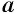 » означает, что
» означает, что 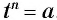 .
.
Корень 3-й степени называется также кубическим.
Например, кубический корень из числа 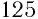 — это число
— это число 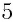 , так как
, так как  . Кубический корень из числа
. Кубический корень из числа 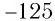 — это число
— это число 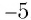 , так как
, так как 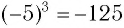 .
.
Корень 7-й степени из числа 128 — это число 2, так как 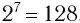 . Корень 7-й степени из числа -128 — это число -2, так как
. Корень 7-й степени из числа -128 — это число -2, так как 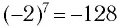 . Корень 7-й степени из числа 0 — это 0, так как
. Корень 7-й степени из числа 0 — это 0, так как 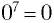 .
.
Во множестве действительных чисел существует единственный корень нечетной степени п из любого числа 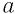 . Этот корень обозначается
. Этот корень обозначается 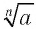
Например, 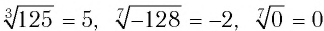 .
.
Утверждение о существовании корня нечетной степени из любого числа мы принимаем без доказательства. Согласно определению, когда п нечетное, то при любом значении а верно равенство 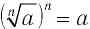
Например, 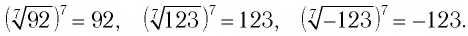
Заметим, что 0 — это единственное число, 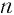 -я степень которого равна 0. Поэтому при любом натуральном
-я степень которого равна 0. Поэтому при любом натуральном 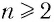 существует единственный корень
существует единственный корень 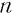 -й степени из 0 — это число 0, т. е.
-й степени из 0 — это число 0, т. е. 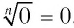 .
.
Примерами корней четной степени могут служить квадратные корни: -7 и 7 — квадратные корни из 49, а -15 и 15 — из 225. Рассмотрим еще несколько примеров. Корни 4-й степени из числа 81 — это числа 3 и -3, так как 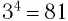 и
и 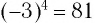 . Корни 6-й степени из числа 64 — это числа 2 и -2, так как
. Корни 6-й степени из числа 64 — это числа 2 и -2, так как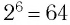 и
и 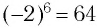 .
.
Во множестве действительных чисел существует ровно два корня четной степени п из любого положительного числа а, их модули равны, а знаки противоположны. Положительный корень обозначается 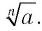
Например,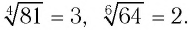
Утверждение о существовании корня четной степени из любого положительного числа мы принимаем без доказательства. Согласно определению, когда 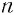 четное, то при любом положительном, значении а верно равенство
четное, то при любом положительном, значении а верно равенство 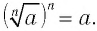
Например, 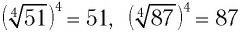 .
.
Не существует такого числа, 4-я степень которого равна -81. Поэтому корня 4-й степени из числа -81 не существует. И вообще, поскольку не существует такого числа, четная степень которого была бы отрицательной, то не существует корня четной степени из отрицательного числа.
Определение:
Неотрицательный корень 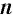 -й степени из числа
-й степени из числа 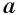 называется арифметическим корнем
называется арифметическим корнем 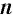 -й степени из
-й степени из 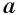 .
.
При четном 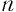 символом
символом 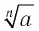 обозначается только арифметический корень
обозначается только арифметический корень 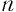 -й степени из числа
-й степени из числа 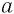 (при чтении записи
(при чтении записи 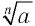 слово «арифметический» обычно пропускают).
слово «арифметический» обычно пропускают).
Выражение, стоящее под знаком корня, называется подкоренным выражением.
Извлечь корень 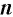 -й степени из числа
-й степени из числа 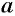 — это значит найти значение выражения
— это значит найти значение выражения 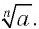
Так как корня четной степени из отрицательного числа не существует, то выражение 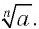 при четном
при четном 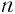 и отрицательном
и отрицательном 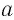 не имеет смысла.
не имеет смысла.
Например, не имеют смысла выражения 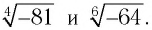
Как мы установили, при любом значении 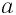 , при котором выражение
, при котором выражение 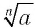 имеет смысл, верно равенство
имеет смысл, верно равенство
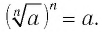 (1)
(1)
Поэтому равенство (1) является тождеством.
В конце XV в. бакалавр Парижского университета Н. Шюке внес усовершенствования в алгебраическую символику. В частности, знаком корня служил символ 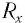 (от латинского слова radix — корень). Так, выражение
(от латинского слова radix — корень). Так, выражение 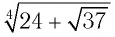 в символике Шюке имело вид
в символике Шюке имело вид 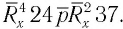
Знак корня 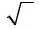 в современном виде был предложен в 1525 г. чешским математиком К. Рудольфом. Его учебник алгебры переиздавался до 1615 г., и по нему учился знаменитый математик Л. Эйлер.
в современном виде был предложен в 1525 г. чешским математиком К. Рудольфом. Его учебник алгебры переиздавался до 1615 г., и по нему учился знаменитый математик Л. Эйлер.
Знак 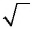 еще называют радикалом.
еще называют радикалом.
Определение корня n-й степени
Корнем 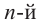 степени
степени 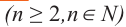 из числа
из числа 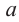 называется число,
называется число, 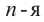 степень которого равна
степень которого равна 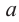 .
.
Например, корнем 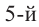 степени из числа
степени из числа 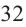 является
является 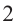 , потому что
, потому что 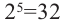 . Корнем
. Корнем 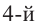 степени из числа
степени из числа 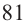 является
является 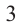 и
и 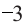 , потому что
, потому что 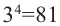 и
и 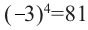 .
.
Если 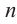 нечетное число, то для любого числа
нечетное число, то для любого числа 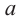 существует единственное действительное число,
существует единственное действительное число, 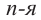 степень которого равна
степень которого равна 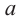 .
.
Если 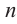 четное число, то при
четное число, то при 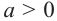 существуют два действительных числа,
существуют два действительных числа, 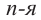 степень которых равна
степень которых равна 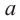 . Эти числа являются взаимно противоположными.
. Эти числа являются взаимно противоположными.
Если 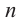 четное число, при
четное число, при 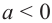
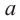 не имеет действительного корня.
не имеет действительного корня.
Арифметическим корнем 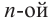 степени из числа
степени из числа 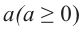 называется неотрицательное число,
называется неотрицательное число, 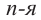 степень которого равна
степень которого равна 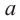 . Обозначается
. Обозначается 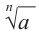 и читается так: «корень
и читается так: «корень 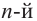 степени из числа
степени из числа 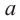 ». Число
». Число 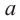 называется подкоренным числом или подкоренным выражением,
называется подкоренным числом или подкоренным выражением, 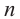 - показателем корня. При
- показателем корня. При 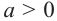 отрицательный корень четной степени из числа
отрицательный корень четной степени из числа 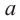 обозначается
обозначается 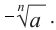
Корень нечетной степени из отрицательного числа можно выразить через арифметический корень той же степени. Например, 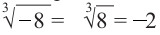
Если 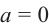 , то
, то 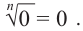
Если 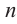 нечетное число, то выражение
нечетное число, то выражение 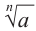 имеет смысл для любого
имеет смысл для любого 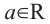
Если 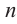 четное число, то выражение
четное число, то выражение 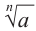 имеет смысл только при
имеет смысл только при 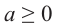
При всех значениях имеющего смысл выражения 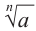 , справедливо
, справедливо 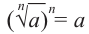
Если 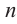 нечетное число,
нечетное число,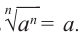 Если
Если 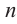 четное число, то
четное число, то 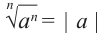
Пример 1: 
Если 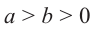 , то
, то 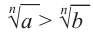
Пример 2: 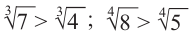
Примеры:
- Уравнение с нечетной степенью
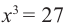 имеет единственный действительный корень:
имеет единственный действительный корень: 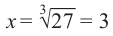
- Уравнение
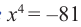 не имеет действительных корней, т.к. степень с четным показателем не равна отрицательному числу.
не имеет действительных корней, т.к. степень с четным показателем не равна отрицательному числу. - Уравнение
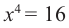 имеет два действительных корня:
имеет два действительных корня: 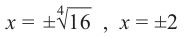
Корень n-й степени и его свойства
Свойство 1.
Если 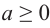 и
и 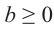 то,
то, 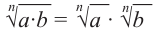
Корень 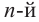 степени из произведения неотрицательных сомножителей равен произведению корней
степени из произведения неотрицательных сомножителей равен произведению корней 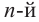 степени сомножителей.
степени сомножителей.
Пример: 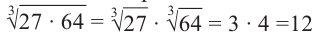
Свойство 2.
Если 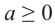 и
и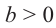 то,
то, 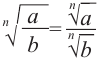
Корень из дроби 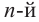 степени с неотрицательным числителем и положительным знаменателем равен отношению корней
степени с неотрицательным числителем и положительным знаменателем равен отношению корней 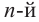 степени числителя и знаменателя.
степени числителя и знаменателя.
Пример: 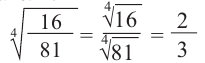
Свойство 3.
Если 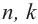 - натуральные числа и
- натуральные числа и 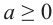 , то
, то 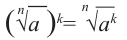
Пример: 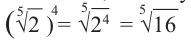
Свойство 4.
Если 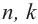 - натуральные числа и
- натуральные числа и 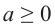 , то
, то 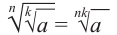
Действительно, при 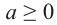 выражения
выражения 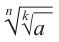 и
и 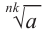 имеют смысл и их значения неотрицательны. Т.к.
имеют смысл и их значения неотрицательны. Т.к. 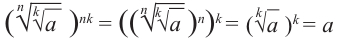 то,
то, 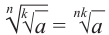
Пример: 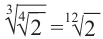
Свойство 5.
Если 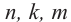 натуральные числа и
натуральные числа и 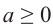 то,
то, 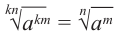 . Если показатель корня и показатель степени подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится. Действительно, согласно свойству 4,
. Если показатель корня и показатель степени подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится. Действительно, согласно свойству 4, 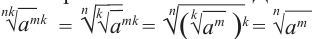
Пример: 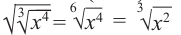
Пример: Вычислите значение выражения 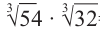
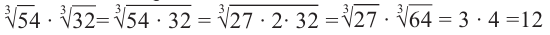
Вынесение множителя из-под знака контроля
Примеры: 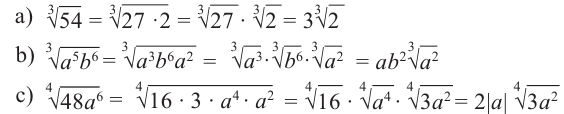
Примеры с решением
Пример №1
Верно ли, что:
а)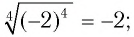 б)
б) 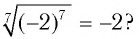
Решение:
а) По определению арифметический корень 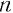 -й степени из неотрицательного числа
-й степени из неотрицательного числа 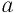 (
(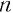 —четное число) является неотрицательным числом,
—четное число) является неотрицательным числом,  -я степень которого равна подкоренному выражению
-я степень которого равна подкоренному выражению 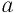 .
.
Поскольку 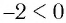 , то равенство
, то равенство 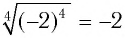 неверное. Верно равенство
неверное. Верно равенство 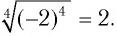
б) По определению корень 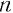 -й степени из числа
-й степени из числа 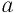 (
(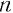 — нечетное число) является числом,
— нечетное число) является числом, 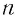 -я степень которого равна подкоренному выражению
-я степень которого равна подкоренному выражению 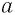 .
.
Поскольку 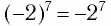 — верное равенство, то равенство
— верное равенство, то равенство 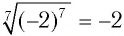 верное.
верное.
Пример №2
Решить уравнение:

Решение:
а) Решением этого уравнения является такое значение 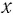 , 3-я степень которого равна 7, т. е. по определению кубического корня имеем:
, 3-я степень которого равна 7, т. е. по определению кубического корня имеем:
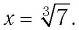
б) Решением этого уравнения является такое значение х, 4-я степень которого равна 5, т. е. (по определению) 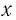 — это корень 4-й степени из числа 5. Но из положительного числа 5 существуют два корня четвертой степени, которые равны по модулю и имеют противоположные знаки. Поскольку положительный корень обозначают
— это корень 4-й степени из числа 5. Но из положительного числа 5 существуют два корня четвертой степени, которые равны по модулю и имеют противоположные знаки. Поскольку положительный корень обозначают 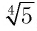 , то второй корень равен
, то второй корень равен 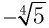 , т. е.
, т. е.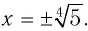
Ответ: 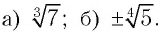
В тетради решение уравнения б) (аналогично и а)) можно записать так:
Решение:
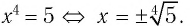
Ответ: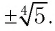
Пример №3
Решить уравнение:

Решение:
а) Число 8 — четное, значит, данное равенство является тождеством при 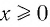 , поэтому каждое неотрицательное значение х является решением (корнем) уравнения
, поэтому каждое неотрицательное значение х является решением (корнем) уравнения 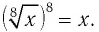
б) Число 13 — нечетное, значит, данное равенство является тождеством при любом значении 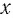 , поэтому решением уравнения
, поэтому решением уравнения 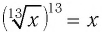 является любое действительное число, a R — множество всех его корней.
является любое действительное число, a R — множество всех его корней.
Ответ: 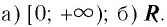
Пример №4
Решить уравнение:
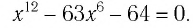
Решение:
Обозначим 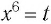 , тогда получим уравнение
, тогда получим уравнение 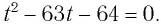
Корни этого уравнения 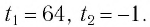
Таким образом, имеем 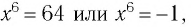
откуда 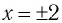 (поясните, почему уравнение
(поясните, почему уравнение 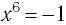 не имеет корней).
не имеет корней).
Ответ: 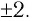
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Тождества с корнями, содержащие одну переменную
- Действия с корнями нечетной степени
- Действия с корнями четной степени
- Бесконечно убывающая геометрическая прогрессия
- Показательные уравнения и неравенства
- Логарифмические уравнения и неравенства
- Степенная функция - определение и вычисление
- Степень с целым показателем