Квадратные неравенства - определение и вычисление с примерами решения

Содержание:

Квадратные неравенства

Неравенства вида:

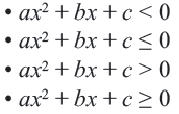
являются квадратными неравенствами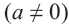

Пример: По графику функции 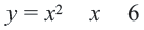напишите множество решений нижеприведенных неравенств.

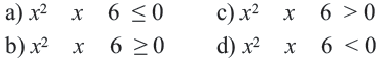
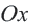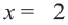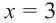График функции, пересекаясь осью в точках и , делит ее на три промежутка, в которых принимает положительные и отрицательные значения. Определим значения выражения 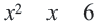в каждом из промежутков.

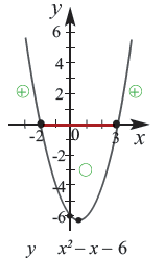
a) График функции 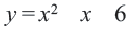пересекает ось 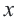в точках 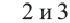и между этими значениями располагается ниже оси 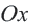. Значит, решение неравенства 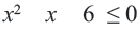будет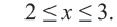

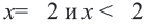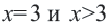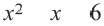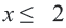b) При значениях или же значения фунции (то есть значение выражения ) равны нулю или же больше нуля. Значит, решением неравенства будет или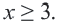

c) Решением неравенства 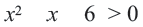будет или же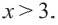

d) Решением неравенства 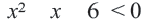будет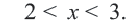

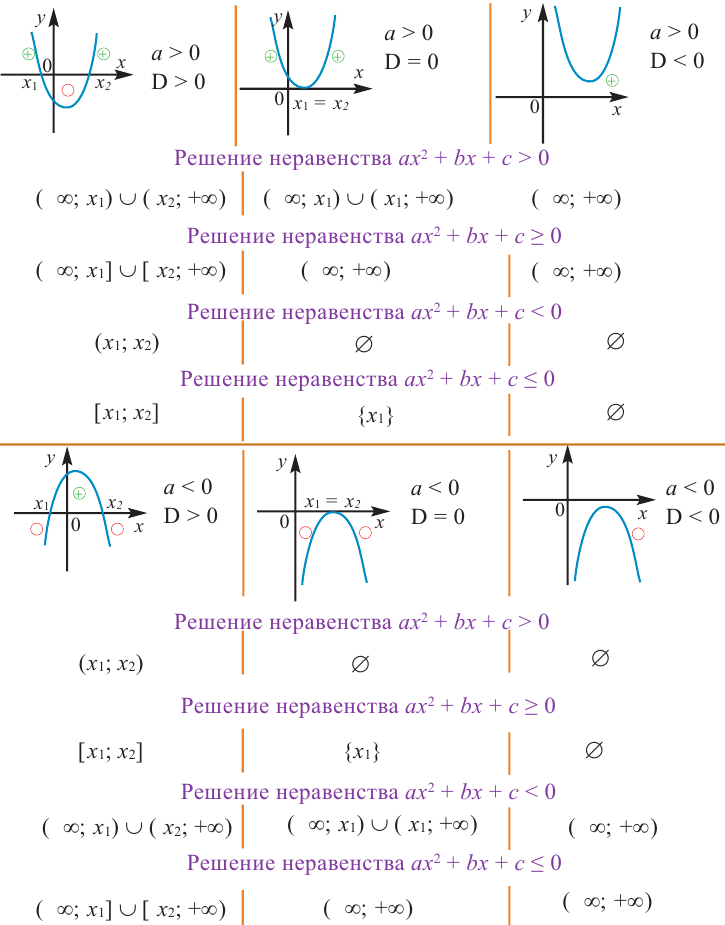
Чтобы решить квадратные неравенства с помощью графика:

1. По значению коэффициента 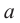выясняется, куда направлены ее ветви (при - вверх, при 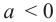- вниз).

2. По значению дискриминанта квадратного трехчлена 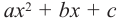выясняется, пересекает ли парабола ось абсцисс в двух точках (при 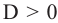), касается ее в одной точке 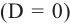, или не имеет общих точек с осью 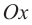(при ).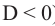

3. По точкам пересечения графика функции с осью 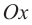схематически изображается график функции.

4. По схематическому изображению графика определяются промежутки, соответствующие решениям данных неравенств.

Пример: Решите неравенство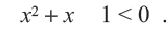

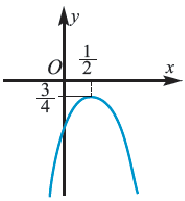
Решение: Ветви параболы направлены вниз 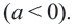Так как уравнение 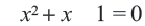не имеет действительных корней, парабола не пересекает ось абсцисс и целиком лежит в нижней полуплоскости. А это значит, что неравенство 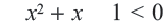верно при любых значениях переменной.

Ответ: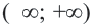

Пример: Решите неравенство .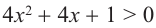

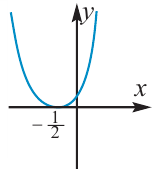
Решение: Изобразим график функции 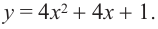Решим уравнение 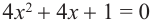и найдем единственное значение переменной, удовлетворяющее уравнению: 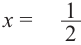. Парабола касается оси 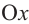в точке 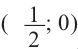. Как видно из графика, это неравенство верно при любых значениях 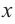, кроме

Ответ: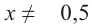

Квадратные неравенства можно решать алгебраическим способом, разложив левую часть на множители и по знаку неравенства исследовать возможные случаи.

Пример. Неравенство 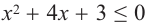запишем в виде 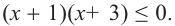Произведение двух множителей будет отрицательным, если множители будут иметь противоположные знаки.

1-ый случай. Предположим, что 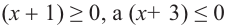. Отсюда 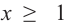и 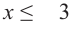. Решением неравенства 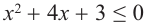будут такие значения 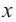, которые удовлетворяют обоим неравенствам. В этом случае такого значения для 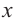нет.

2-ой случай. Предположим что 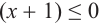и 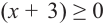. Решив эти неравенства, получим 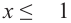и .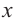

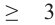Все значения промежутка от 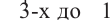, включая 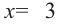и . Являются решением неравенства 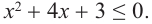Ответ: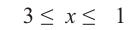

Решение неравенств методом интервалов

Метод интервалов

1. Напишите уравнение, соответствующее неравенству.

2. Найдите корни уравнения. Отметьте на числовой оси точки, соответствующие корням уравнения. Эти точки называются граничными точками неравенства.

3. В каждом из интервалов, образованных граничными точками, выберите пробные точки и определите какой из интервалов, будет решением неравенства.

Пример. Решите неравенство :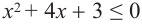

Для того чтобы решить неравенство:

1) Находим корни уравнения :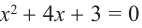

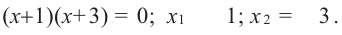
2. Отмечаем на числовой оси точки 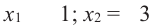. Как видно, граничные точки делят числовую ось на 3 интервала.

3. В каждом из интервалов выбираем пробное число 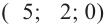и проверяем неравенство.

4. Запишем решение.

Исследование 1. Исследуем изменение знаков в интервалах при решении неравенств, в левой части которых произведение множителей вида 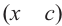, а в правой 0.

Пример. 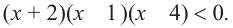Из уравнения 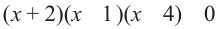найдем 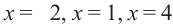. На числовой оси отметим граничные точки и в каждом интервале (начиная с 1-го правого) определим знак выражения .

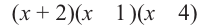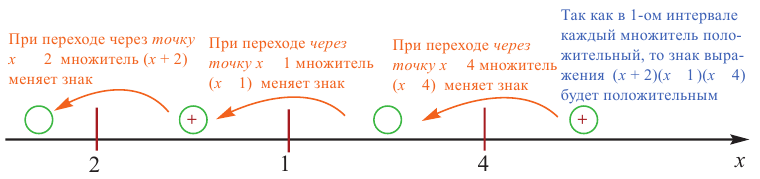
Как видно, в этом случае знаки на числовой оси при переходе из одного интервала в другой чередуются.

Решением неравенства будут промежутки со знаком минус.

Ответ: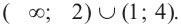

Если каждый множитель имеет вид , тогда в первом нравом интервале знак произведения положительный. Если каждый множитель первой степени, то в интервалах знаки чередуются.

Исследование 2. Неравенства, содержащие множители четной степени вида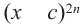 и изменения знаков в интервалах.

Пример.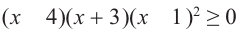

1) Найдем граничные точки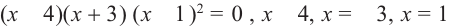

2) Отметим граничные точки на числовой оси

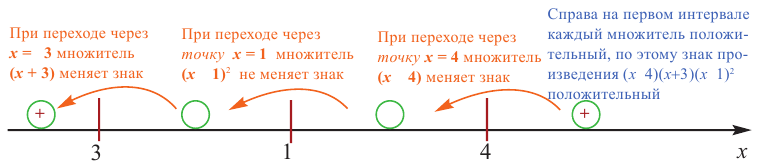
Из-за множителя 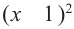в правой и левой окрестностях точки 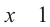знак в промежутках повторяется. Неравенство справедливо в промежутках со знаком 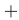и в граничных точках. Ответ: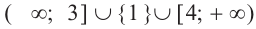

Если в неравенстве есть множители с четным показателем степени вида 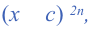то справа и слева от граничной точки 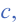знак повторяется.

• Заказать решение задач по высшей математике

Решение неравенств методом интервалов

1. Напишите неравенство в виде эквивалентного неравенства, в одной части которого рациональное выражение, а в другой части нуль.

2. Найдите значение переменных, при которых числитель и знаменатель рационального выражения обращается в нуль. Эти значения переменных являются граничными точками данного неравенства.

3. Из интервалов, образованных граничными точками, последовательно выберите пробные точки и проверьте, какие из этих интервалов принадлежат множеству решений неравенства.

Пример.

1)

2) Найдем нули числителя и знаменателя: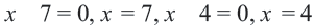

3) Отмечая точк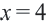и и 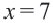на числовой оси, делим ее на три интервала. Эти точки называются граничными точками.

Выберем пробные точки и проверим неравенство

Так как при 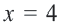знаменатель обращается в нуль, то эта точка не входит в множество решений, а точка 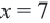в это множество входит. 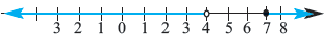Множество решений неравенства 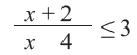будет 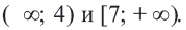Ответ: 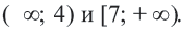Замечание: Неравенство 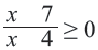можно также решить, применив правило изменения знаков в интервалах.