
Из генеральной совокупности, распределенной по нормальному закону, извлечена выборка объема 𝑛 = 12:
 |
 |
Математическая статистика |
 |
 |
Решение задачи |
 |
 |
|
 |
 |
Выполнен, номер заказа №16444 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
|
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл! |
|
Закажите у меня новую работу, просто написав мне в чат! |
Из генеральной совокупности, распределенной по нормальному закону, извлечена выборка объема 𝑛 = 12:
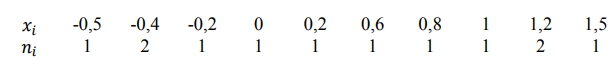
Оценить с надежностью 0,95 математическое ожидание 𝑎 нормально распределенного признака генеральной совокупности с помощью доверительного интервала.
Решение
Среднее 𝑥̅в равно Выборочная дисперсия равна Найдем выборочную несмещённую 𝑆 2 (исправленную) дисперсию: Исправленное среднее квадратическое отклонение равно: Доверительный интервал для математического ожидания 𝑎 равен: значение, определяемое по таблице квантилей распределения Стьюдента в зависимости от числа степеней свободы (𝑛 − 1 = 11) и доверительной вероятности . По таблице квантилей распределения Стьюдента находим: и искомый доверительный интервал имеет вид: Ответ:

Похожие готовые решения по математической статистике:
- По результатам 10 измерений емкости конденсатора прибором, не имеющим систематической ошибки, получили следующие отклонения от номинального
- Исходя из предположения о нормальном распределении данной случайной величины, найти доверительный интервал для среднего
- Задан интервальный вариационный ряд нормально распределенного признака. Найти доверительные интервалы, покрывающие неизвестное
- Выполнены многократные измерения длины объекта. Требуется построить доверительный интервал с надежностью 𝛾 для оценки математического
- Среднее время сборки изделия составляло 90 минут. Инженер изобрел новый метод сборки этого изделия, и продолжительность сборки 10 изделий новым
- Исходя из предположения о нормальном распределении данной случайной величины, найти доверительный интервал для среднего значения случайной
- При исследовании проницаемости сосудов сетчатки была получена следующая выборка: 14, 12, 16, 11, 15, 17, 13, 15, 16, 11. Считая, что данный признак
- С помощью микроскопа измеряли диаметр эритроцитов человека. При этом были получены следующие значения: 5, 8, 11, 8 мкм. Дайте интервальную
- В урне находится 4 белых, 3 красных и 7 черных шаров. Наудачу вынимаются 3 шара. Найти вероятность того, что из них окажется: а) 2 белых
- Двухмерный случайный вектор равномерно распределен внутри выделенной жирными прямыми линиями на рис. 3 области B . Двухмерная плотность
- Вычислить математическое ожидание и дисперсию величин U и V , а так же определить их коэффициент корреляции
- Случайным образом выбирают 3 шара из 9, среди которых 3 белых и 6 черных. Найти вероятность того, что среди выбранных окажется два белых шара.

