
Двойные и тройные интегралы - определение и вычисление с примерами решения
Содержание:
Двойные и тройные интегралы
Понятие двойного интеграла
В теории определенного интеграла для нахождения площади криволинейной трапеции было введено понятие интегральной суммы, пределом которой является определенный интеграл. На основе задачи об определении объема тела мы придем к понятию двумерной интегральной суммы, предел которой называется двойным интегралом.
Пример:
Найти объем тела, ограниченного сверху непрерывной поверхностью z = f(x, у) (f(x, у) 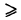
Тело указанного вида для краткости называется цилиндроидом. В частном случае, когда верхнее основание цилиндроида есть плоскость, параллельная нижнему основанию его, то цилиндроид называется цилиндром. Примером цилиндра служит круговой цилиндр, рассматриваемый в средней школе. Обобщая рассуждение, обычно применяемое для нахождения объема кругового цилиндра, нетрудно доказать, что объем V цилиндра с площадью основания S и высотой Н равен V = SH.
Для вычисления объема V данного цилиндроида разобьем основание его S на конечное число элементарных ячеек 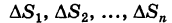 (вообще говоря, криволинейных). В каждой из этих ячеек
(вообще говоря, криволинейных). В каждой из этих ячеек 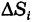 выберем точку
выберем точку 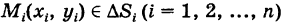 и построим прямой цилиндрический столбик с основанием
и построим прямой цилиндрический столбик с основанием 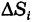 и высотой
и высотой 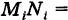
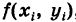 , равной аппликате поверхности в выбранной точке.
, равной аппликате поверхности в выбранной точке.
Объем такого столбика на основании формулы объема цилиндра, очевидно, равен

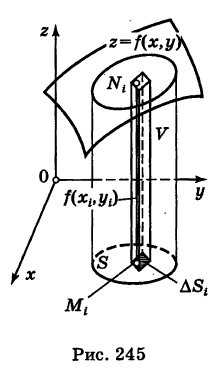
где 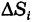 — площадь соответствующей ячейки. Сумма объемов этих цилиндрических столбиков представляет собой объем ступенчатого тела, приближенно заменяющего данное криволинейное тело, причем аппроксимация является, вообще говоря, тем более точной, чем меньше диаметры ячеек
— площадь соответствующей ячейки. Сумма объемов этих цилиндрических столбиков представляет собой объем ступенчатого тела, приближенно заменяющего данное криволинейное тело, причем аппроксимация является, вообще говоря, тем более точной, чем меньше диаметры ячеек 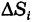 . Поэтому объем нашего цилиндроида приближенно выразится суммой
. Поэтому объем нашего цилиндроида приближенно выразится суммой
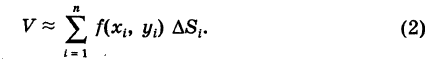
Формула (2) дает возможность найти объем V с любой степенью точности, если число ячеек 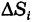 достаточно велико и линейные размеры их весьма малы. Обозначим через d1 диаметр ячейки
достаточно велико и линейные размеры их весьма малы. Обозначим через d1 диаметр ячейки 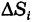 т. е. наибольший линейный размер ее. Точнее говоря, под диаметром d ограниченной замкнутой (т. е. с присоединенной границей) фигуры Ф (дуги, площадки и т. п.) понимается длина наибольшей ее хорды АВ, где
т. е. наибольший линейный размер ее. Точнее говоря, под диаметром d ограниченной замкнутой (т. е. с присоединенной границей) фигуры Ф (дуги, площадки и т. п.) понимается длина наибольшей ее хорды АВ, где 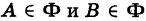 (рис. 246).
(рис. 246).
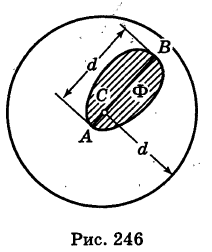
Из данного определения следует, что фигура Ф, имеющая диаметр d, целиком помещается внутри круга радиуса d, описанного из любой ее точки С как из центра. Поэтому если 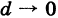 , то фигура Ф «стягивается в точку». Аналогично определяется диаметр пространственного тела.
, то фигура Ф «стягивается в точку». Аналогично определяется диаметр пространственного тела.
Пусть
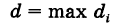
— наибольший из диаметров ячеек 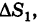
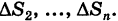 Предполагая, что в формуле (2) число ячеек п неограниченно возрастает
Предполагая, что в формуле (2) число ячеек п неограниченно возрастает 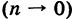 , причем диаметр наибольшей из них становится сколь угодно малым
, причем диаметр наибольшей из них становится сколь угодно малым 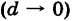 , в пределе получаем точную формулу для объема цилиндроида
, в пределе получаем точную формулу для объема цилиндроида
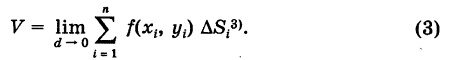
Здесь мы для удобства ячейки и их площади обозначаем одинаковыми буквами. Разница между ними видна из контекста.
Ячейки 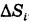 можно предполагать замкнутыми.
можно предполагать замкнутыми.
Точнее говоря, по определению под объемом цилиндроида понимается предел (3), если он существует.
Выражение, стоящее в правой части формулы (3), называется двойным интегралом от функции f(x, у), распространенным на область S, и обозначается следующим образом:
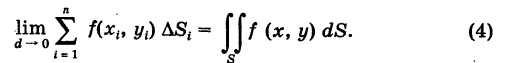
Поэтому для объема цилиндроида окончательно имеем
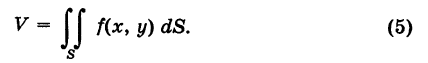
Обобщая конструкцию, примененную для вычисления объема цилиндроида, приходим к следующим определениям.
Определение: Двумерной интегральной суммой (2) от данной функции f(x9 у)> распространенной на данную область S, называется сумма парных произведений площадей элементарных ячеек 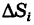 области S на значения
области S на значения 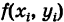 функции f(x, у) в выделенных точках этих ячеек (рис. 247).
функции f(x, у) в выделенных точках этих ячеек (рис. 247).
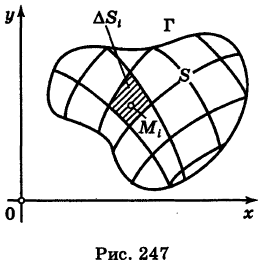
Определение: Двойным интегралом (4) от функции f(x, у), распространенным на данную область S, называется предел соответствующей двумерной интегральной суммы (2) при неограниченном возрастании числа п элементарных ячеек 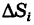 и стремлении к нулю их наибольшего диаметра d при условии, что этот предел существует и не зависит от способа дробления области S на элементарные ячейки
и стремлении к нулю их наибольшего диаметра d при условии, что этот предел существует и не зависит от способа дробления области S на элементарные ячейки 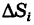 и выбора точек в них.
и выбора точек в них.
В формуле (4) у) называется подынтегральной функцией, S — областью интегрирования, a dS — элементом площади. Справедлива следующая теорема:
Теорема: Если область S с кусочно-гладкой границей Г ограничена и замкнута, а функция f(x, у) непрерывна в области S, то двойной интеграл
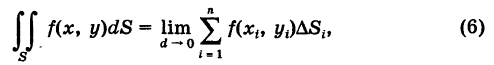
существует, т. е. предел соответствующей двумерной интегральной суммы существует и не зависит от способа дробления области S на элементарные ячейки 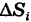 , и выбора точек в них.
, и выбора точек в них.
В дальнейшем мы будем предполагать, что условия этой теоремы выполнены.
В формуле (6) нет необходимости указывать, что 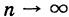 , так как из
, так как из 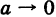 , очевидно, следует
, очевидно, следует 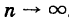 .
.
Если f(x, у) 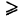 0, то двойной интеграл (6) представляет собой объем прямого цилиндроида, построенного на области S как на основании и ограниченного сверху поверхностью z = f(x, у) (геометрический смысл двойного интеграла).
0, то двойной интеграл (6) представляет собой объем прямого цилиндроида, построенного на области S как на основании и ограниченного сверху поверхностью z = f(x, у) (геометрический смысл двойного интеграла).
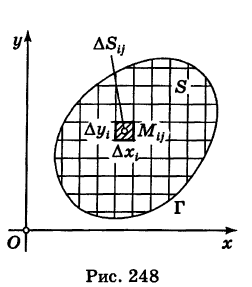
Так как значение двойного интеграла не зависит от вида элементарных ячеек, то в дальнейшем при решении задач мы будем использовать это обстоятельство, выбирая наиболее подходящие сетки. Весьма часто удобной оказывается прямоугольная сетка, образованная пересечением двух систем прямых, параллельных соответственно координатным осям Ох и Оу (рис. 248). В этом случае элементарными ячейками 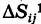 являются прямоугольники со сторонами, равными
являются прямоугольники со сторонами, равными 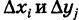 , за исключением, возможно, ячеек, примыкающих к границе Г.
, за исключением, возможно, ячеек, примыкающих к границе Г.
Чтобы подчеркнуть использование прямоугольной сетки, в обозначении интеграла (4) полагают
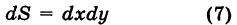
(двумерный элемент площади в прямоугольных координатах), причем
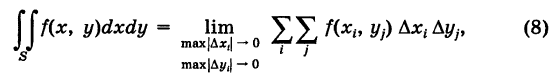
где 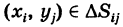 и сумма (8) распространяется на все значения i и для которых
и сумма (8) распространяется на все значения i и для которых 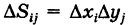 (можно показать, что непрямоугольные ячейки, примыкающие к кусочно-гладкой границе Г, не влияют на значение предела (8)).
(можно показать, что непрямоугольные ячейки, примыкающие к кусочно-гладкой границе Г, не влияют на значение предела (8)).
В следующих параграфах мы рассмотрим основные способы вычисления двойного интеграла.
Здесь мы применяем двойную индексацию ячеек, указывая отдельно номер i вертикальной полосы и номер j горизонтальной полосы, содержащих данную ячейку, подобно тому, как на билете в кино отмечается номер ряда и номер места.
Двойной интеграл в прямоугольных декартовых координатах
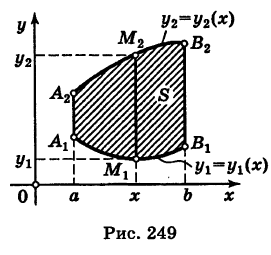
Предположим для определенности, что область интегрирования S представляет собой криволинейную трапецию (рис. 249);
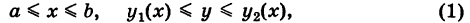
где 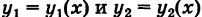 — однозначные непрерывные функции на отрезке
— однозначные непрерывные функции на отрезке 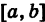 . Такую область будем называть стандартной относительно оси Оу. Заметим, что вертикаль, проходящая через точку х оси Ох при а < х < Ь, пересекает границу Г области S только в двух точках
. Такую область будем называть стандартной относительно оси Оу. Заметим, что вертикаль, проходящая через точку х оси Ох при а < х < Ь, пересекает границу Г области S только в двух точках 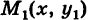 («точка входа») и
(«точка входа») и 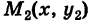 («точка выхода»).
(«точка выхода»).
Пусть f(x, у) — функция, непрерывная в области S, и
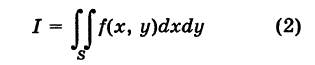
— ее двойной интеграл.
1) Предположим сначала, что 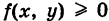 в области S. Тогда двойной интеграл I представляет собой объем цилиндроида (рис. 250), ограниченного снизу областью S, сверху поверхностью z = f(x, у) и с боков прямой цилиндрической поверхностью.
в области S. Тогда двойной интеграл I представляет собой объем цилиндроида (рис. 250), ограниченного снизу областью S, сверху поверхностью z = f(x, у) и с боков прямой цилиндрической поверхностью.
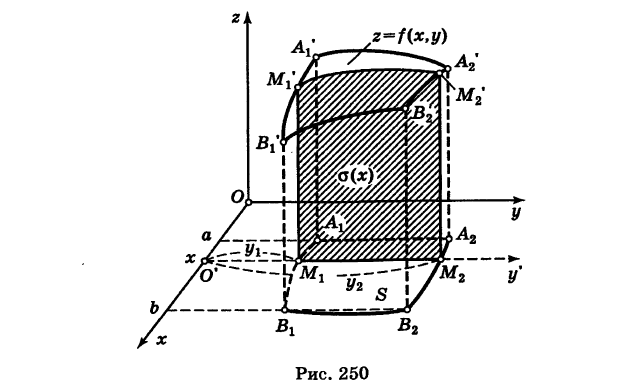
Для вычисления объема I применим метод сечений. А именно, пусть а(х) — площадь сечения цилиндроида плоскостью 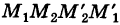 перпендикулярной оси Ох в точке ее
перпендикулярной оси Ох в точке ее 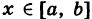 (рис. 250).
(рис. 250).
Тогда имеем

Но а(х) представляет собой площадь криволинейной трапеции, ограниченной снизу отрезком 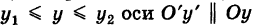 и сверху кривой z = f(x, у) х = const. Поэтому
и сверху кривой z = f(x, у) х = const. Поэтому
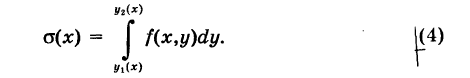
Можно доказать, что при наших условиях а(х) непрерывна при 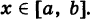
Подставляя выражение (4) в формулу (3), получим окончательно
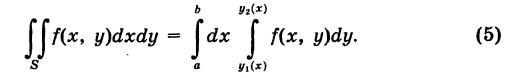
Таким образом, двойной интеграл равен соответствующему повторному интегралу (5), т. е. вычисление двойного интеграла сводится к двум квадратурам. Заметим, что при вычислении внутреннего интеграла в формуле (5) х рассматривается как постоянная величина.
2) В случае знакопеременной функции z = f(x, у), например, если 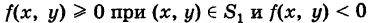
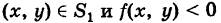 , двойной интеграл (2) равен алгебраической сумме объемов
, двойной интеграл (2) равен алгебраической сумме объемов 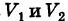 цилиндроидов, построенных соответственно на основаниях
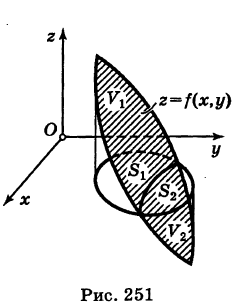
цилиндроидов, построенных соответственно на основаниях 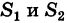 (рис. 251), т. е.
(рис. 251), т. е.
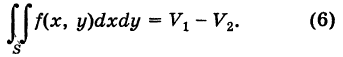
Можно доказать, что формула (5) справедлива и в этом случае.
Отметим один важный случай: пусть S — прямоугольник 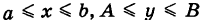 (рис. 252) и
(рис. 252) и 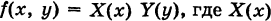 — функция, непрерывная на
— функция, непрерывная на 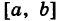 и зависящая только от х, и
и зависящая только от х, и 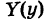 — функция, непрерывная на [А, Б] и зависящая только от у. В силу формулы (5) имеем
— функция, непрерывная на [А, Б] и зависящая только от у. В силу формулы (5) имеем
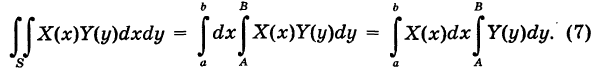
Но внутренний интеграл в формуле (7) есть постоянное число, поэтому его можно вынести за знак внешнего интеграла и мы получим
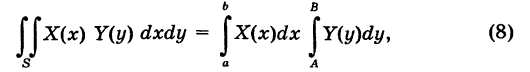
т. е. двойной интеграл (8) равен произведению двух однократных интегралов.
Замечание 1. Если область S — стандартная относительно оси Ох, т. е. (рис. 253)
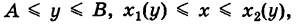
то по аналогии с формулой (5) получаем
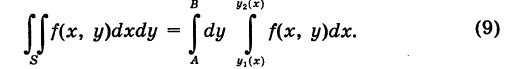
В частности, если область S есть прямоугольник: 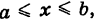
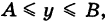 то имеем
то имеем
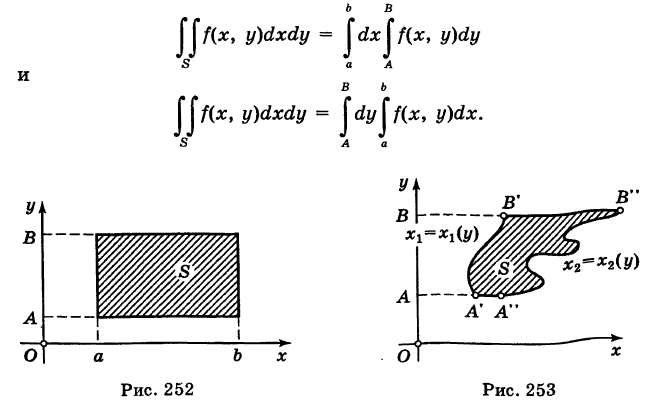
Отсюда получаем
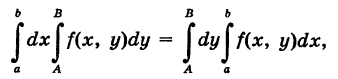
т е. если пределы интегрирования в повторном интеграле от непрерывной функции конечны и постоянны, то результат интегрирования не зависит от порядка интегрирования.
Замечание 2. Если область S нестандартная, то ее разбивают (если это возможно) на конечное число областей 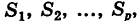 стандартных относительно осей координат Ох или Оу и на основании свойства пределов полагают
стандартных относительно осей координат Ох или Оу и на основании свойства пределов полагают
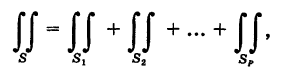
а затем применяют соответственно формулы (5) или (9).
Пример:
Найти
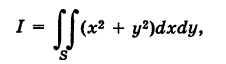
где S — квадрат 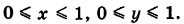
Решение:
Расставляя пределы интегрирования, будем иметь
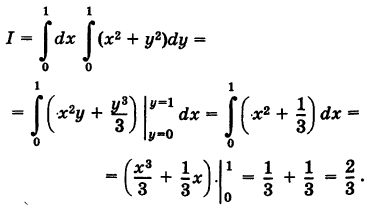
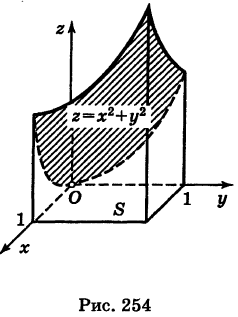
Геометрически / представляет собой объем цилиндроида с квадратным нижним основанием, ограниченного сверху параболоидом вращения 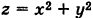 (рис. 254).
(рис. 254).
Пример:
Вычислить двойной интеграл
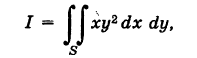
где S — прямоугольник 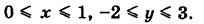
Решение:
Расставляя пределы интегрирования и разделяя переменные, будем иметь
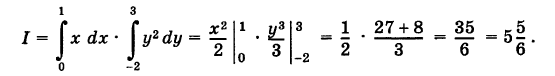
Пример:
Вычислить

где S — треугольник с вершинами О (0, 0), А (2, 0) и В (2, 1) (рис. 255).
Решение:
Область S ограничена прямыми у = 0, у = х/2, х = 2 и является стандартной как относительно оси Оу, так и оси Ох.
Для вертикали MN «точка входа» в область S есть М(х, 0), «точка выхода» — N(x, х/2) (0 < х < 2). Таким образом, при фиксированном х переменная у для точек области S меняется от 0 до х/2. Поэтому, интегрируя в двойном интеграле (10) сначала по у при х = const, а затем по x, согласно формуле (5) будем иметь
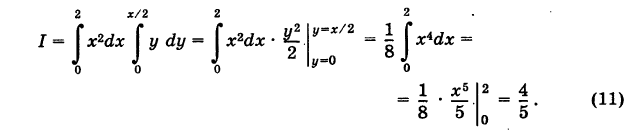
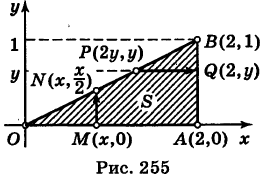
Аналогично, для горизонтали PQ «точка входа» в область есть Р{2у, у) и «точка выхода» — Q (2, у) (0 < у < 1). Следовательно, при фиксированном у переменная х для точек области S меняется от 2у до 2. Произведя в двойном интеграле (10) интегрирование сначала по х при у = const, а затем по у, на основании формулы (9) получаем
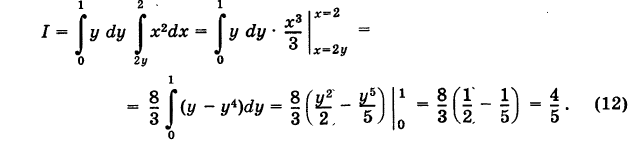
Мы пришли, как и следовало ожидать, к тому же самому результату, причем второй способ вычисления оказался несколько более сложным.
Пример:
Изменить порядок интегрирования в повторном интег- рале
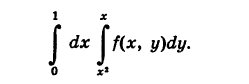
Область интегрирования S ограничена кривыми у= х2, у = х и х = 0, х = 1 (рис. 256). Отсюда, изменяя роли осей координат, получаем
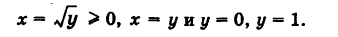
Следовательно,
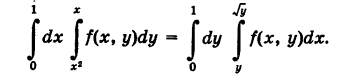
Пример:
Расставить пределы интегрирования в двойном интеграле
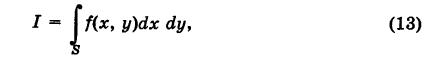
если область интегрирования 5 есть круговое кольцо, ограниченное окружностями 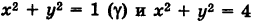 (Г) (рис. 257). Область S не является стандартной. Для расстановки пределов интегрирования в интервале (13) разбиваем область S на четыре стандартные относительно оси OY области
(Г) (рис. 257). Область S не является стандартной. Для расстановки пределов интегрирования в интервале (13) разбиваем область S на четыре стандартные относительно оси OY области 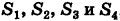 как указано на рисунке. Используя уравнение окружностей
как указано на рисунке. Используя уравнение окружностей
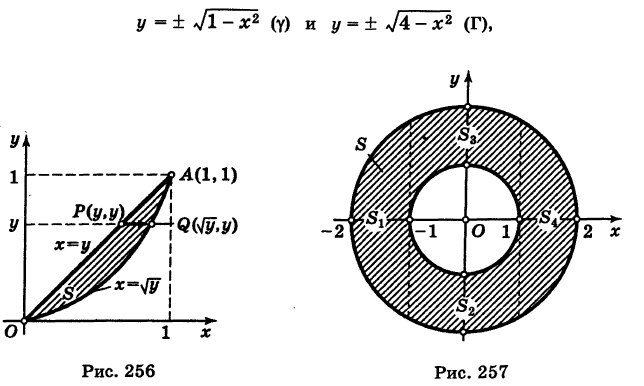
имеем
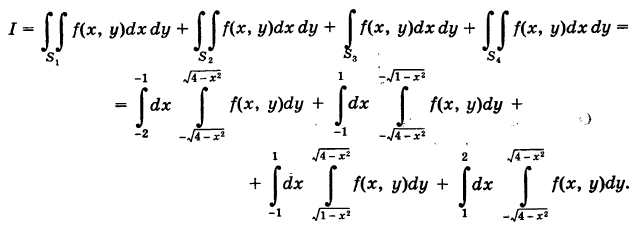
Аналогичная формула получится, если мы будем расставлять пределы интегрирования в другом порядке.
Двойной интеграл в полярных координатах
Пусть в двойном интеграле
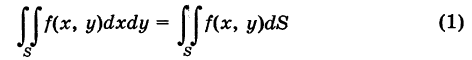
при обычных предположениях мы желаем перейти к полярным координатам г и ф, полагая
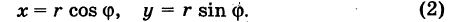
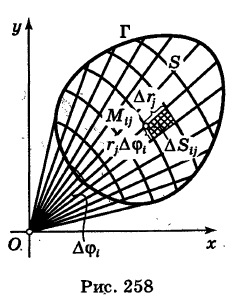
Область интегрирования S разобьем на элементарные ячейки 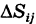 с помощью координатных линий
с помощью координатных линий 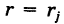 (окружности) и ф
(окружности) и ф 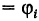 (лучи) (рис. 258).
(лучи) (рис. 258).
Введем обозначения
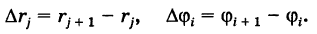
Так как окружность перпендикулярна (ортогональна) радиусам, то внутренние ячейки 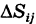 с точностью до бесконечно малых высшего порядка малости относительно их площади можно рассматривать как прямоугольники с измерениями
с точностью до бесконечно малых высшего порядка малости относительно их площади можно рассматривать как прямоугольники с измерениями 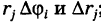 ; поэтому площадь каждой такой ячейки будет равна
; поэтому площадь каждой такой ячейки будет равна
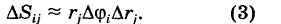
Что касается ячеек AS^ неправильной формы, примыкающих к границе Г
области интегрирования S, то эти ячейки не повлияют на значение двойного интеграла и мы их будем игнорировать.
В качестве точки 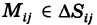 для простоты выберем вершину ячейки
для простоты выберем вершину ячейки 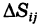 с полярными координатами
с полярными координатами 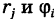 . Тогда декартовы координаты точки
. Тогда декартовы координаты точки 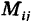 равны
равны
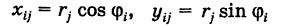
и, следовательно,
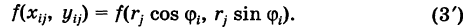
Двойной интеграл (1) представляет собой предел двумерной интегральной суммы, причем можно показать, что на значение этого предела не влияют добавки к слагаемым интегральной суммы, являющиеся бесконечно малыми высшего порядка малости. Поэтому, учитывая формулы (3) и (3'), получаем
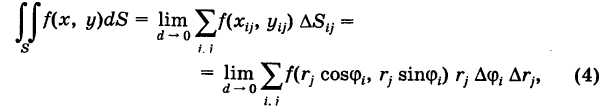
где d — максимальный диаметр ячеек 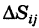 и сумма распространена на все ячейки указанного выше вида, целиком содержащиеся в области S. С другой стороны, величины суть числа и их можно рассматривать как прямоугольные декартовы координаты некоторых точек плоскости
и сумма распространена на все ячейки указанного выше вида, целиком содержащиеся в области S. С другой стороны, величины суть числа и их можно рассматривать как прямоугольные декартовы координаты некоторых точек плоскости 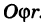 . Таким образом, сумма (4) является интегральной суммой для функции
. Таким образом, сумма (4) является интегральной суммой для функции
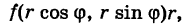
соответствующая прямоугольной сетке с линейными элементами 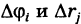 . Следовательно,
. Следовательно,
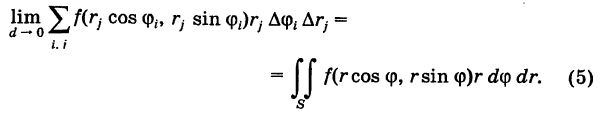
Выравнивая формулы (4) и (5), получаем окончательно
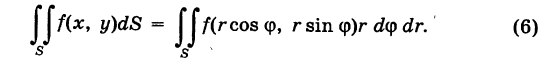
Выражение

называется двумерным элементом площади в полярных координатах. Итак, чтобы в двойном интеграле (1) перейти к полярным координатам, достаточно координаты х и у заменить по формулам (2), а вместо элемента площади dS подставить выражение (7).
Для вычисления двойного интеграла (6) его нужно заменить повторным. Пусть область интегрирования S определяется неравенствами
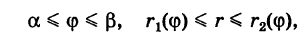
где 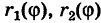 — однозначные непрерывные функции на отрезке
— однозначные непрерывные функции на отрезке 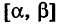 (рис. 259). Тогда по аналогии с прямоугольными координатами имеем
(рис. 259). Тогда по аналогии с прямоугольными координатами имеем
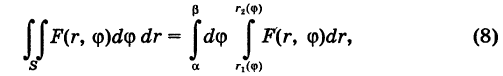
где
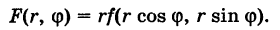
Пример:
Переходя к полярным координатам 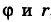 , вычислить двойной интеграл
, вычислить двойной интеграл
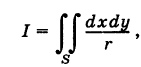
где S — первая четверть круга радиуса R = 1 с центром в точке О (0, 0) (рис. 260).
Так как 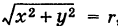 , то, применяя формулу (6), получаем
, то, применяя формулу (6), получаем
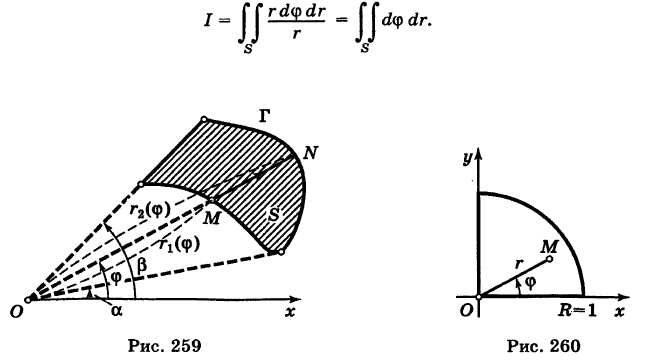
Область S определяется неравенствами 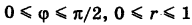 . Поэтому на основании формулы (8) имеем
. Поэтому на основании формулы (8) имеем
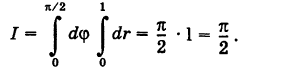
Пример:
В интеграле
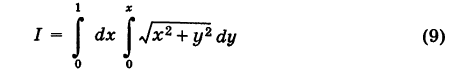
перейти к полярным координатам.
Область интегрирования здесь есть треугольник S, ограниченный прямыми у=0, у = х, х = 1 (рис. 261).
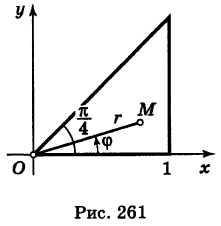
В полярных координатах уравнения этих прямых записываются следующим образом: 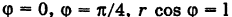 и, следовательно, область S определяется неравенствами
и, следовательно, область S определяется неравенствами
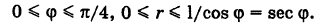
Отсюда на основании формул (6) и (8), учитывая, что 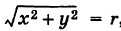 , имеем
, имеем
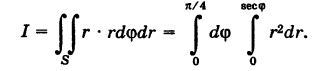
Интеграл Эйлера—Пуассона
С помощью полярных координат можно просто вычислить важный для теории вероятностей интеграл Эйлера— Пуассона

Так как определенный интеграл не зависит от обозначения переменной интегрирования, то, очевидно, можно также записать

Перемножая формулы (1) и (2) и учитывая, что произведение этих однократных интегралов можно рассматривать как двойной интеграл от произведения подынтегральных функций, будем иметь
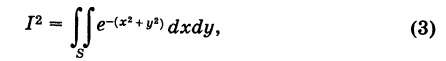
где область S определяется неравенствами
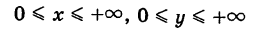
и, следовательно, представляет собой первый квадрант координатной плоскости Оху (рис. 262).
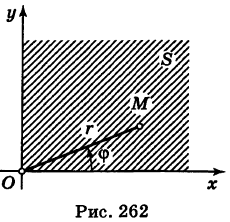
Переходя в интеграле (3) к полярным координатам, получим
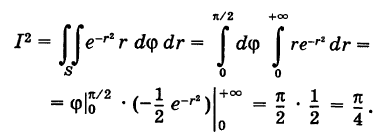
Отсюда, учитывая положительность числа 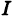 , находим
, находим
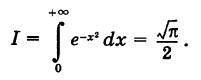
В силу четности функции 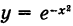 имеем также
имеем также
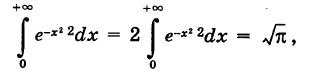
что представляет собой площадь, ограниченную осью Ох и кривой Гаусса 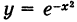 (см, рис. 120).
(см, рис. 120).
Теорема о среднем
Пусть функция f(x, у) непрерывна в ограниченной замкнутой области 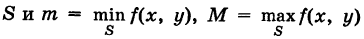 — соответственно наименьшее и наибольшее значения функции f(x, у) в области S.
— соответственно наименьшее и наибольшее значения функции f(x, у) в области S.
Для двумерной интегральной суммы этой функции, распространенной на область S, имеем оценки
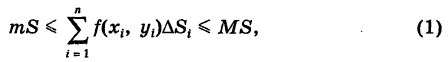
где 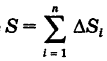 — площадь области S. Отсюда, переходя к пределу при
— площадь области S. Отсюда, переходя к пределу при 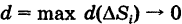 в неравенствах (1) и учитывая существование двойного интеграла, получаем
в неравенствах (1) и учитывая существование двойного интеграла, получаем
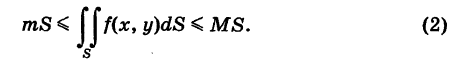
Число

называется средним значением функции 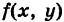 в области S. Из неравенств (2) вытекает, что
в области S. Из неравенств (2) вытекает, что 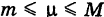 .
.
Формулу (3) можно переписать в следующем виде:

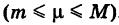 . Таким образом, двойной интеграл равен среднему значению подынтегральной функции, умноженной на площадь области интегрирования.
. Таким образом, двойной интеграл равен среднему значению подынтегральной функции, умноженной на площадь области интегрирования.
Не нужно думать, что формула (4) дает универсальный способ вычисления двойного интеграла. Дело в том, что, как правило, среднее значение функции определяется через двойной интеграл. Поэтому реальный смысл здесь имеет оценка (2).
Пример:
Оценить интеграл
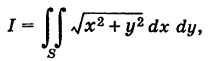
где S — квадрат 
Для функции f(x, у) = 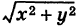 имеем
имеем
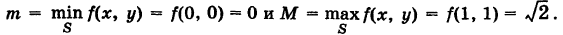
Так как S = 1, то 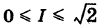 = 1,41. Можно принять
= 1,41. Можно принять
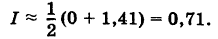
Эта оценка грубая, так как точное значение интеграла есть
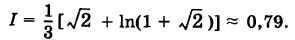
Более точное значение интеграла I получится, если область интегрирования S разбить на достаточно мелкие части и к каждой из них применить теорему о среднем.
Геометрические приложения двойного интеграла
Прямой цилиндроид, построенный на основании S в координатной плоскости Оху и ограниченный сверху непрерывной поверхностью z = f(x, у), имеет объем, равный
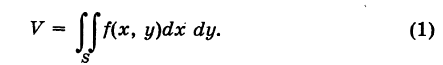
Пример:
Найти объем 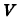 тела, ограниченного поверхностями
тела, ограниченного поверхностями
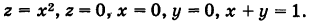
Решение:
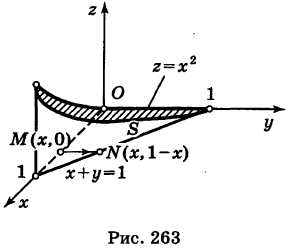
Искомое тело имеет своим основанием треугольник S на плоскости Оху у образованный линиями 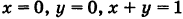 ,и ограничено сверху параболическим цилиндром
,и ограничено сверху параболическим цилиндром 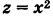 (рис. 263). Отсюда на основании формулы (1) получим
(рис. 263). Отсюда на основании формулы (1) получим
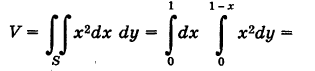
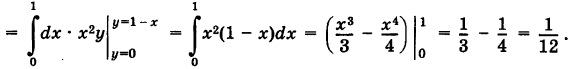
Если в формуле (1) положить
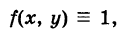
то получим объем прямого цилиндра с высотой 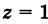 , численно равный площади S его основания. Поэтому площадь плоской области S равна
, численно равный площади S его основания. Поэтому площадь плоской области S равна

Формулу (2) можно записать также в виде

Пример:
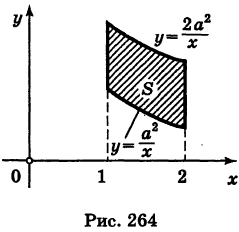
Найти площадь, ограниченную гиперболами 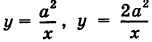 (а > 0) и прямыми х = 1, х = 2 (рис. 264).
(а > 0) и прямыми х = 1, х = 2 (рис. 264).
Решение:
На основании формулы (2) получим, что площадь S равна
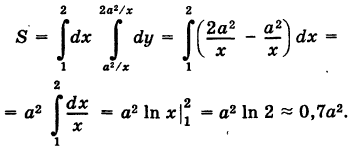
Физические приложения двойного интеграла
Пусть S — материальная пластинка. Если 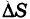 есть часть пластинки S, содержащая точку М и имеющая массу
есть часть пластинки S, содержащая точку М и имеющая массу 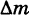 , то отношение
, то отношение
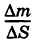
называется средней поверхностной плотностью куска 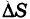 а предел этого отношения при условии, что диаметр
а предел этого отношения при условии, что диаметр 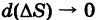 , называется поверхностной плотностью р(М) пластинки S в точке М:
, называется поверхностной плотностью р(М) пластинки S в точке М:
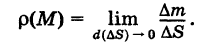
Очевидно, поверхностная плотность р(М) пластинки S есть функция точки М. Понятия средней поверхностной плотности пластинки и поверхностной плотности пластинки в данной точке
вполне аналогичны понятиям средней линейной плотности дуги и линейной плотности дуги в точке, введенным.
Положим, что поверхностная плотность пластинки S в текущей точке М(х, у) равна 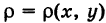 , где
, где 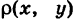 — известная непрерывная функция. Рассмотрим бесконечно малый элемент dS пластинки, содержащий точку М (рис. 265). Так как в пределах этого элемента пластинку можно считать однородной с плотностью р, то масса элемента dS (элементарная масса) равна
— известная непрерывная функция. Рассмотрим бесконечно малый элемент dS пластинки, содержащий точку М (рис. 265). Так как в пределах этого элемента пластинку можно считать однородной с плотностью р, то масса элемента dS (элементарная масса) равна

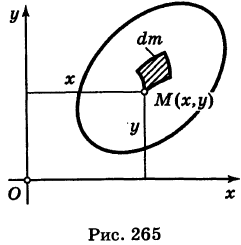
Интегрируя выражение (1) по всей пластинке S, находим массу пластинки

Рассматривая dm как материальную точку, удаленную от осей координат Ох и Оу на расстояния у их, получим элементарные статические моменты пластинки
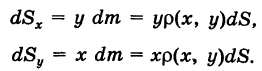
Отсюда, интегрируя эти выражения по всей пластинке S, находим статические моменты пластинки S относительно координатных осей
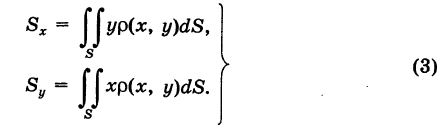
В механике доказывается, что статический момент пластинки относительно какой-нибудь оси совпадает со статическим моментом точечной массы, равной массе пластинки, сосредоточенной в центре масс ее относительно той же оси (теорема Вариньона). Отсюда, обозначая через (х0, у0) координаты центра масс пластинки S, будем иметь
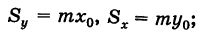
следовательно,
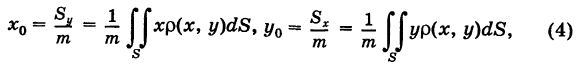
где 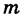 — масса (2) пластинки.
— масса (2) пластинки.
Аналогично, для элементарных моментов инерции пластинки S относительно осей координат Ох и Оу получаем выражения
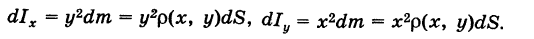
Отсюда после интегрирования по пластинке S будем иметь моменты инерции пластинки S относительно координатных осей
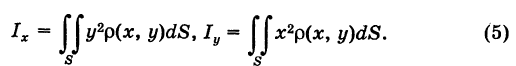
Элементарный полярный момент инерции определяется формулой
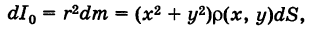
где 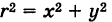 — квадрат расстояния массы dm от начала координат. Интегрируя последнее выражение по пластинке S, получаем полярный момент пластинки
— квадрат расстояния массы dm от начала координат. Интегрируя последнее выражение по пластинке S, получаем полярный момент пластинки
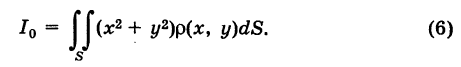
Из формул (5) и (6) следует, что

Полагая 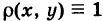 в формулах моментов, получим соответствующие моменты инерции геометрической фигуры S. Напомним, что при вычислении в декартовых прямоугольных координатах, как обычно, принимается dS = dx dy, а в случае полярных координат имеем
в формулах моментов, получим соответствующие моменты инерции геометрической фигуры S. Напомним, что при вычислении в декартовых прямоугольных координатах, как обычно, принимается dS = dx dy, а в случае полярных координат имеем 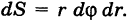
Пример:
Определить координаты центра масс квадратной пластинки S: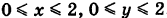 , поверхностная плотность которой в точке
, поверхностная плотность которой в точке 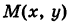 равна р = х + у.
равна р = х + у.
Решение:
Пользуясь формулой (2), находим массу пластинки
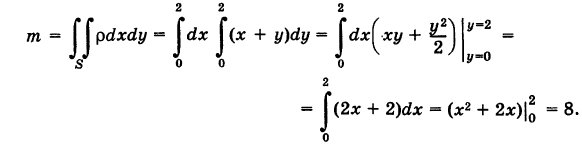
По формуле (3) определяем статические моменты пластинки S относительно координатных осей:
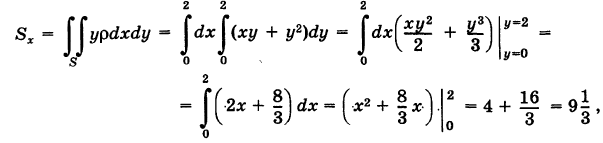
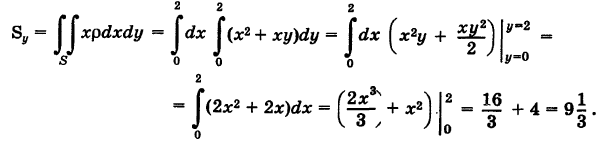
Равенство моментов 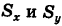 можно было предвидеть ввиду симметрии задачи.
можно было предвидеть ввиду симметрии задачи.
На основании формул (4) центр масс пластинки S имеет координаты
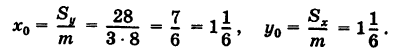
Пример:
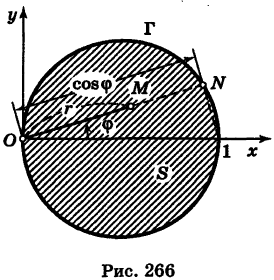
Найти момент инерции 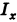 круга S:
круга S: 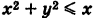 (рис. 266) относительно оси Ох.
(рис. 266) относительно оси Ох.
Решение:
Полагая р = 1, на основании первой формулы (5) имеем

Задачу будем решать в полярных координатах. Имеем
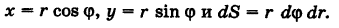
Уравнение границы Г области S есть
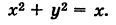
Отсюда, переходя к полярным координатам, получаем 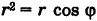 . Следовательно, после сокращения на несущественный множитель г имеем
. Следовательно, после сокращения на несущественный множитель г имеем
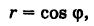
причем так как 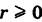 , то
, то 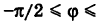
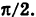 Таким образом, при каждом фиксированном
Таким образом, при каждом фиксированном 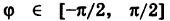 радиус г меняется в пределах О
радиус г меняется в пределах О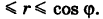 Переходя к полярным координатам в формуле (8), получаем
Переходя к полярным координатам в формуле (8), получаем
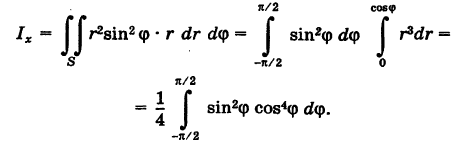
Как известно, 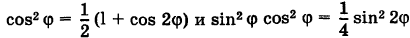 поэтому
поэтому
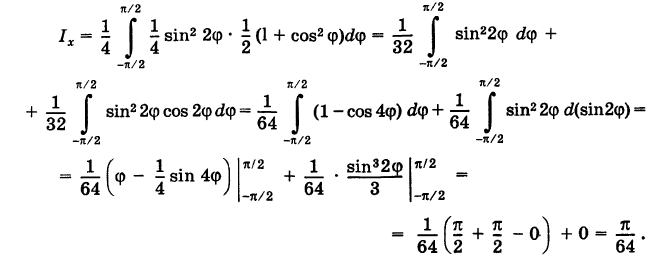
Понятие о тройном интеграле
По аналогии с двойным интегралом определяется так называемый тройной интеграл. Пусть в декартовом пространстве Охуz задана конечная замкнутая область V и f(x, у, z) — ограниченная функция, определенная в V. Разобьем область V на конечное число ячеек 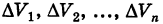 и в каждой из них выберем точку
и в каждой из них выберем точку
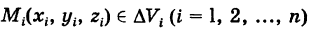
(рис. 267). Сумма
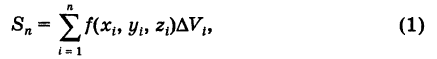
где 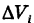 — объем i-й ячейки, называется трехмерной интегральной суммой.
— объем i-й ячейки, называется трехмерной интегральной суммой.
Обозначим через d наибольший из диаметров ячеек 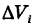 . Будем произвольным способом неограниченно измельчать ячейки
. Будем произвольным способом неограниченно измельчать ячейки 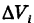 . Тогда предел интегральной суммы (1) при
. Тогда предел интегральной суммы (1) при 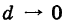 , если этот предел существует и не зависит от формы ячеек
, если этот предел существует и не зависит от формы ячеек 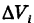 и выбора точек
и выбора точек 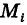 в них, называется тройным интегралом
в них, называется тройным интегралом
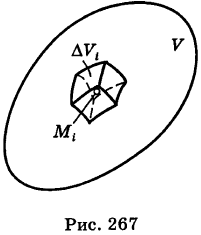
от функции 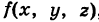 , распространенным на область V, и обозначается следующим образом:
, распространенным на область V, и обозначается следующим образом:
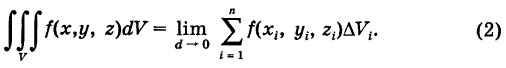
Доказывается, что если подынтегральная функция 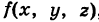 непрерывна в замкнутой ограниченной области интегрирования V с кусочно-гладкой границей, то тройной интеграл (2) существует.
непрерывна в замкнутой ограниченной области интегрирования V с кусочно-гладкой границей, то тройной интеграл (2) существует.
Если область V заполнена массой и 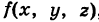 представляет собой непрерывно распределенную объемную плотность в текущей точке
представляет собой непрерывно распределенную объемную плотность в текущей точке 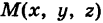 , то
, то 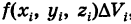 где
где 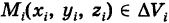 с точностью до бесконечно малой высшего порядка малости относительно максимального объема ячеек
с точностью до бесконечно малой высшего порядка малости относительно максимального объема ячеек 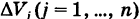 есть масса ячейки
есть масса ячейки 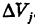 . Следовательно, интегральная сумма (1) приближенно равна массе т, заполняющей область V. При
. Следовательно, интегральная сумма (1) приближенно равна массе т, заполняющей область V. При 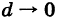 получаем, что предел суммы Sn будет равен массе т. Отсюда выводим физический смысл тройного интеграла: если
получаем, что предел суммы Sn будет равен массе т. Отсюда выводим физический смысл тройного интеграла: если 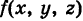 есть непрерывная плотность распределения массы в пространстве Oxyz, то тройной интеграл
есть непрерывная плотность распределения массы в пространстве Oxyz, то тройной интеграл
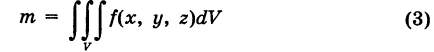
представляет собой массу, заполняющую область интегрирования V. В частности, если плотность f(x, у, z) 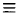 1, то масса области V численно равна ее объему. Поэтому объем области V выражается тройным интегралом
1, то масса области V численно равна ее объему. Поэтому объем области V выражается тройным интегралом

Если вычисление тройного интеграла (2) ведется в прямоугольных координатах х, у, z, то в качестве ячеек 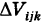 выбирают прямоугольные параллелепипеды с измерениями
выбирают прямоугольные параллелепипеды с измерениями 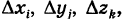 грани которых параллельны координатным плоскостям, т. е. полагают
грани которых параллельны координатным плоскостям, т. е. полагают
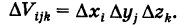
В этом случае элемент объема dV считают равным

(элемент объема в прямоугольных координатах) и тройной интеграл (2) записывают в следующем виде:
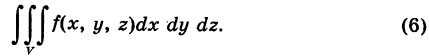
В частности, для объема тела получаем формулу
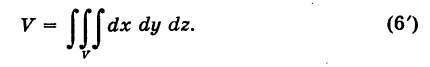
В простейшем случае вычисление тройного интеграла (6) сводится к трем квадратурам. А именно, пусть область интегрирования Г стандартна относительно оси Oz, т. е. ограничена снизу и сверху соответственно однозначными непрерывными поверхностями
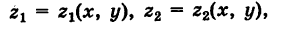
причем проекция области V на координатную плоскость Оху есть плоская область S (рис. 268).
Отсюда следует, что при фиксированных значениях (х, у) 6 S соответствующие аппликаты z точек области V изменяются в пределах 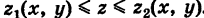 По аналогии с двойным интегралом будем иметь
По аналогии с двойным интегралом будем иметь
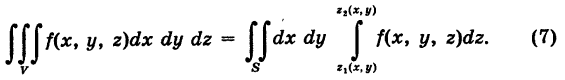
Если, кроме того, проекция S стандартна относительно оси Оу и определяется неравенствами
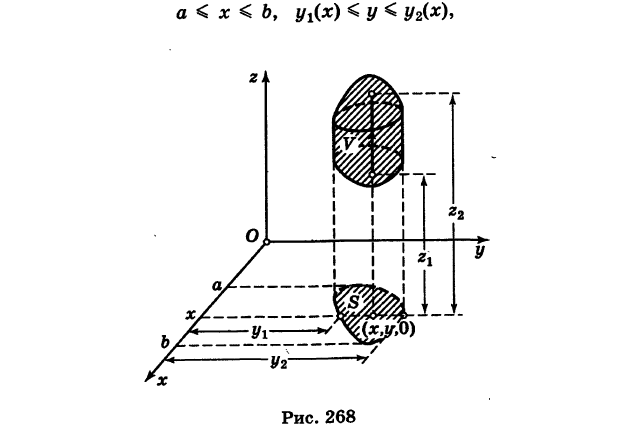
где 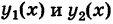 — однозначные непрерывные функции на отрезке
— однозначные непрерывные функции на отрезке 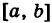 , то
, то
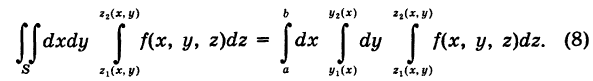
Из формул (7) и (8) получаем окончательно
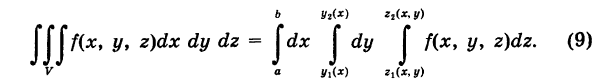
Таким образом, вычисление тройного интеграла сводится к трем квадратурам.
Заметим, что если область интегрирования V стандартна относительно всех трех координатных осей Ох, Оу и Oz, то пределы интегрирования для тройного интеграла (6) можно расставить 3! = 6 различными способами.
Пример:
Вычислить
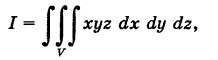
где V — пирамида OPQR, ограниченная следующими плоскостями:
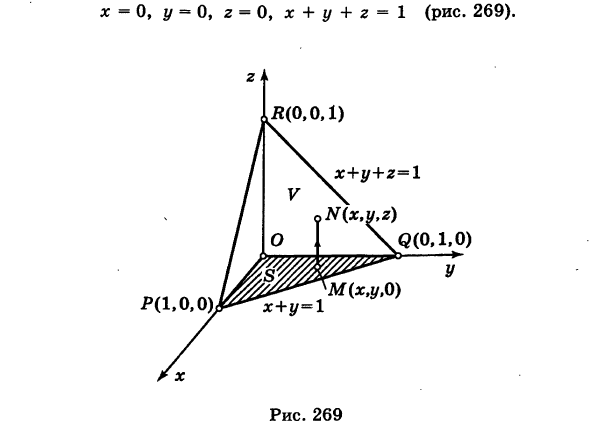
Решение:
Проекция области V на координатную плоскость Оху есть треугольник S, ограниченный прямыми
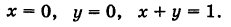
При 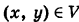 аппликаты точек
аппликаты точек 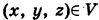 удовлетворяют неравенству
удовлетворяют неравенству 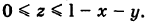 Поэтому
Поэтому
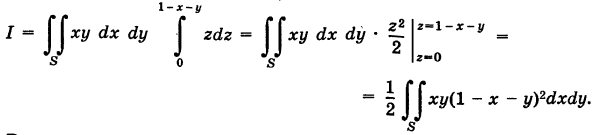
Расставляя пределы интегрирования для треугольника S, получаем
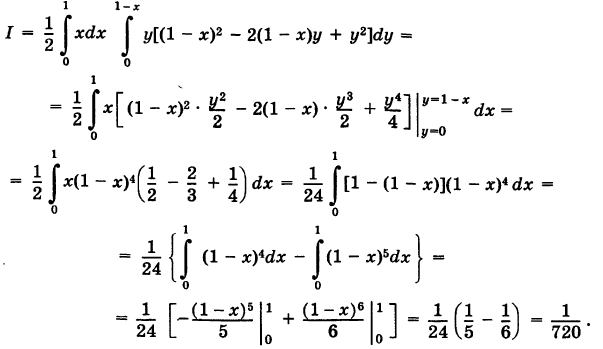
Число I представляет собой массу пирамиды V, если плотность ее в текущей точке 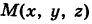 равна
равна 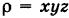 .
.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |