
Понятие о производной вектор-функции - определение с примером решения
Содержание:
Понятие о производной вектор-функции
Пусть мы имеем вектор-функцию
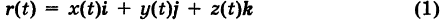
(а < t < 
Естественно определим предел вектор-функции, полагая 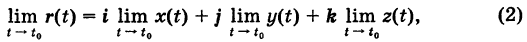 если пределы в правой части равенства (2) существуют.
если пределы в правой части равенства (2) существуют.
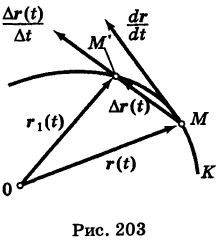
Дадим параметру t приращение 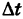 ; тогда точка М(х, у, z) кривой К переместится в точку этой кривой
; тогда точка М(х, у, z) кривой К переместится в точку этой кривой 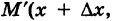
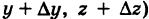 , радиус-вектор которой есть
, радиус-вектор которой есть
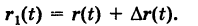
Из векторного треугольника ОММ' имеем (рис. 203)
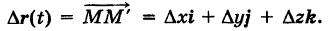
Отсюда, предполагая для определенности, что 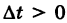 , получим
, получим
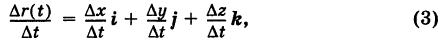
т. е. вектор 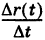 направлен по секущей
направлен по секущей 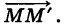
В общем случае при 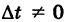 вектор
вектор 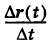 будет коллинеарен вектору
будет коллинеарен вектору 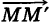 .
.
Определение: Под производной вектор-функции 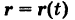 понимается вектор
понимается вектор

Если 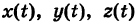 — дифференцируемые функции, то из формулы (3) при
— дифференцируемые функции, то из формулы (3) при 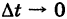 находим
находим
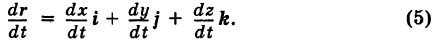
Так как предельное положение секущей по определению есть касательная, то вектор 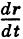 направлен по касательной к кривой К
направлен по касательной к кривой К
в точке ее М (в сторону возрастания параметра t). Из формулы (5), как обычно, получаем
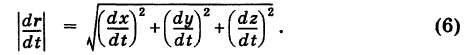
Если t — время, то вектор 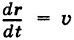 представляет собой скорость движущейся точки
представляет собой скорость движущейся точки  , понимаемую как вектор.
, понимаемую как вектор.
Пример:
Написать уравнение касательной к кривой 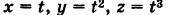 в точке ее
в точке ее 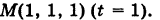
Решение:
Здесь
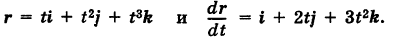
Отсюда направление касательной в точке М определяется вектором
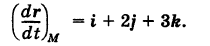
Таким образом, уравнение искомой касательной есть
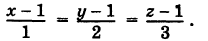
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |