
Интегрирование иррациональных функций с примерами решения
Содержание:
Интегрирование иррациональных функций.
Определение 1. Функция вида 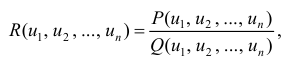
Пример 1.
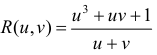 - рациональная функция переменных u и v, при этом:
- рациональная функция переменных u и v, при этом:
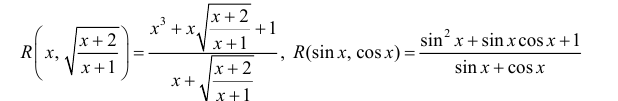
п.1. Интегралы вида:

Пусть s – общий знаменатель дробей 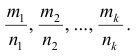 Тогда подстановка
Тогда подстановка 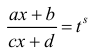
делает подинтегральную функцию рациональной.
Пример 2.
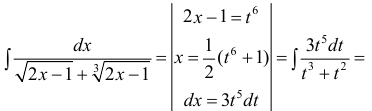
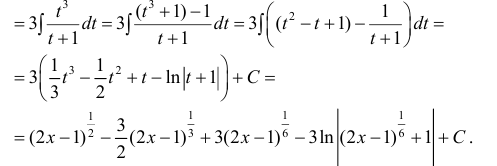
Пример 3
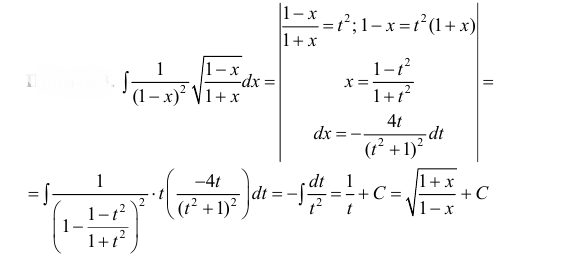
п.2. Интегралы вида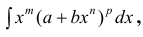
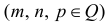 - интегралы от дифференциального бинома.
- интегралы от дифференциального бинома.
Интегралы вида (1) выражаются через элементарные функции в следующих случаях:
а) p∈Z - интегралы рассмотрены в п.1.
б) 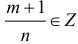 , тогда подстановка
, тогда подстановка 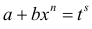 , где s – знаменатель р приводит интегральную функцию к рациональной.
, где s – знаменатель р приводит интегральную функцию к рациональной.
в) 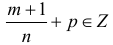 , тогда подстановка
, тогда подстановка 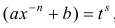 , где s – знаменатель р приводит интегральную функцию к рациональной.
, где s – знаменатель р приводит интегральную функцию к рациональной.
Во всех других случаях интегралы (1) выразить через элементарные функции нельзя (теорема Чебышева).
Пример 4.
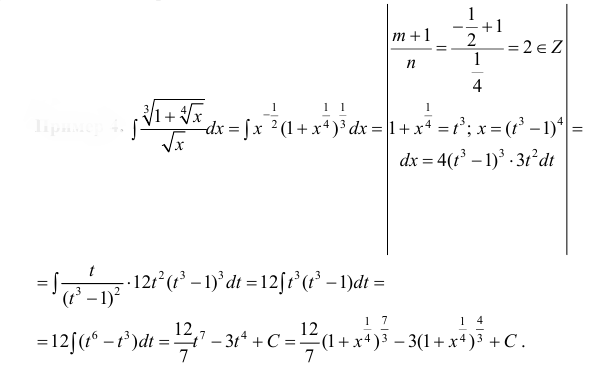
Пример 5.
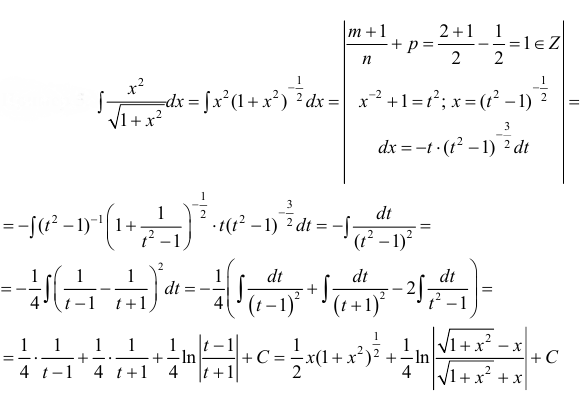
п.3. Интегралы вида 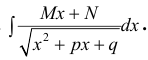 Вычисление интегралов проводится аналогично интегралам
Вычисление интегралов проводится аналогично интегралам 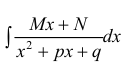 выделением полного квадрата в трехчлене
выделением полного квадрата в трехчлене
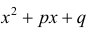 (см. § 21, примеры 1, 2).
(см. § 21, примеры 1, 2).
Пример 6.
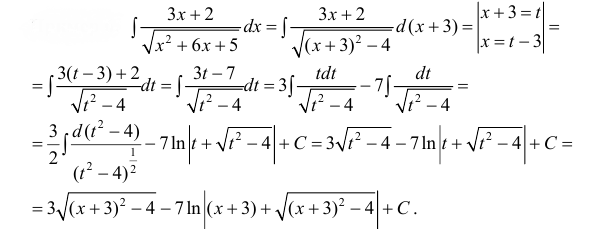
п 4. Интегралы вида 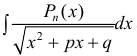 , где
, где 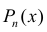 - многочлен степени n.
- многочлен степени n.
Для вычисления интегралов используют равенство:
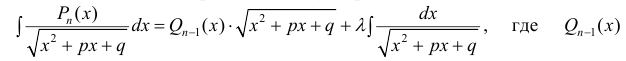 многочлен степени n−1 . Коэффициенты многочлена
многочлен степени n−1 . Коэффициенты многочлена 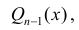 а также число λ находятся, если продифференцировать правую и левую часть равенства (2).
а также число λ находятся, если продифференцировать правую и левую часть равенства (2).
Пример 7.
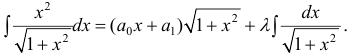 После взятия производной:
После взятия производной:
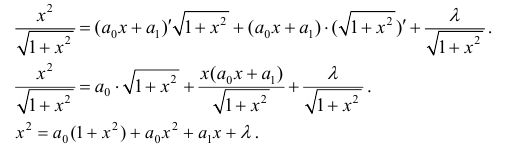
Приравниваем друг к другу коэффициенты при одинаковых степенях х в правой и левой частях.

Решив систему (3), получим :
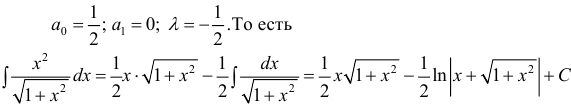
(сравни с примером 5).
п.5. Интегралы вида 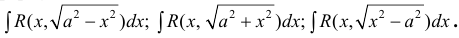
В данных интегралах можно избавиться от иррациональности, если применить подходящую тригонометрическую или гиперболическую подстановку.
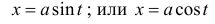 - для первого интеграла,
- для первого интеграла,
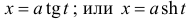 - для второго,
- для второго,
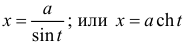 - для третьего (см. § 23).
- для третьего (см. § 23).
Пример 8.
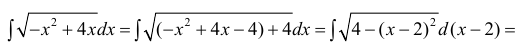
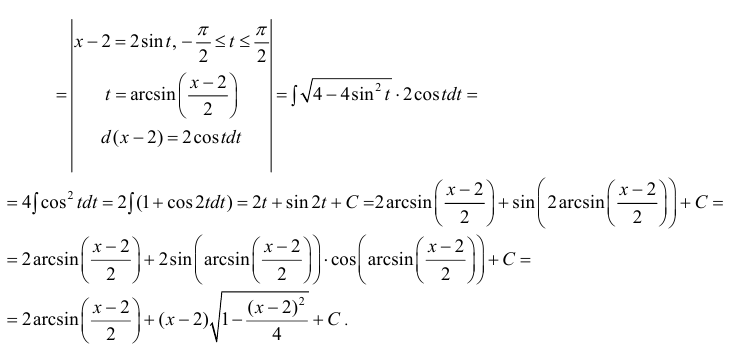
Пример 9.

Интегрирование некоторых иррациональных функций
1. Интегралы вида 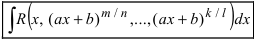 .
.
Интегралы такого типа вычисляются по следующей схеме:
- -у дробей
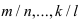 находят наименьший общий знаменатель, который обозначим через р;
находят наименьший общий знаменатель, который обозначим через р; - - проводят замену
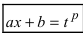 .
.
В результате приведенных действий данный интеграл переходит в неопределенный интеграл от рациональной функции.
Пример:
Вычислить 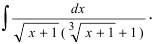
Решение:
В данном примере 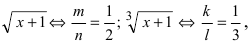 следовательно, наименьший общий знаменатель этих дробей равен 6. Таким образом.
следовательно, наименьший общий знаменатель этих дробей равен 6. Таким образом.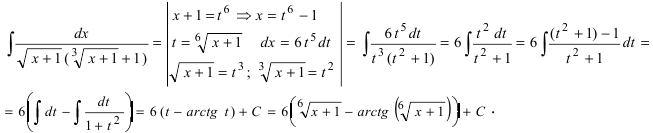
2. Интегралы вида 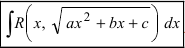 .
.
Такие интегралы путем замены 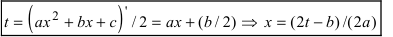 приводятся к одному из интегралов вида:
приводятся к одному из интегралов вида:
1. 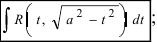 2.
2.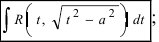 3.
3.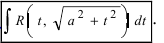
Для вычисления этих интегралов применяют следующие тригонометрические замены
1. 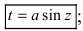 2.
2.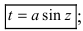 3.
3. 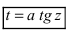 - которые позволяют избавиться от квадратного корня.
- которые позволяют избавиться от квадратного корня.
Пример:
Вычислить 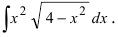
Решение:
Данный интеграл соответствует интегралам типа 1., поэтому
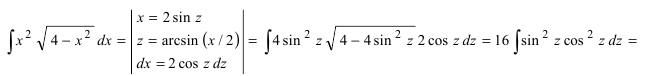
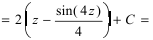
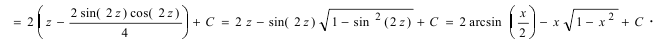
Пример:
Вычислить 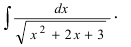
Решение:
Воспользуемся указанной выше заменой
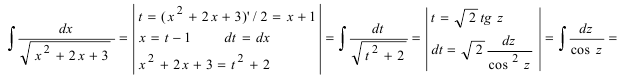
(интеграл вычислен в п. 2а) 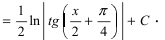
Пример:
Вычислить 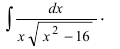
Решение:
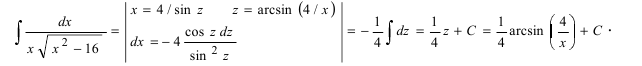
Пример:
Вычислить 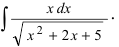
Решение:
Воспользуемся указанной выше заменой
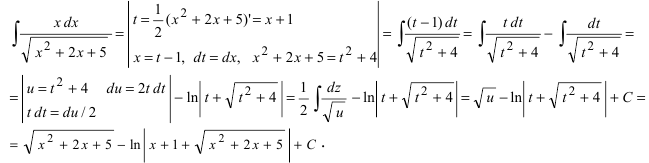
Понятие о неберущихся интегралах
Определение: Интегралы, первообразные которых не выражаются через элементарные функции, называются неберущимися: 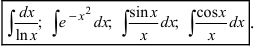
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |