
Интегрирование тригонометрических функций с примерами решения
Содержание:
Интегрирование тригонометрических функций
Универсальная тригонометрическая подстановка
При вычислении неопределенных интегралов от рациональной функции, зависящей только от тригонометрических функций применяется универсальная тригонометрическая подстановка, применение которой обосновано следующими формулами, связывающими функции синуса и косинуса с тангенсом половинного аргумента 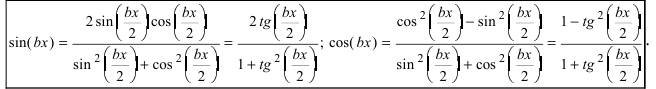
При исчислении интегралов вида 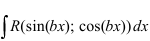
Пример:
Вычислить 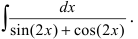
Решение:
Воспользуемся универсальной тригонометрической подстановкой 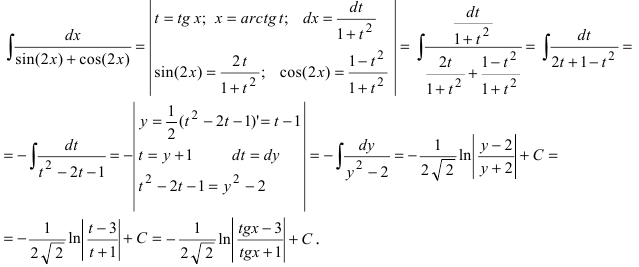
Замечание: Отметим, что универсальную тригонометрическую подстановку следует применять не во всех случаях. Для некоторых типов интегралов от тригонометрических функций, которые будут рассмотрены ниже, существуют более простые способы вычисления.
2. Интегралы вида 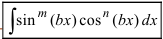 (
(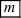 и
и 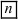 - целые числа)
- целые числа)
а). Если хотя бы одно из чисел m или n является нечетным целым числом, то от нечетной степени отделяют один множитель, а оставшуюся четную часть выражают через другую тригонометрическую фу нкцию с помощью основного тригонометрического тождества 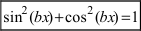 , при этом надо помнить, что
, при этом надо помнить, что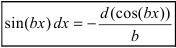 , а
, а 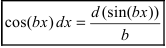 .
.
Пример:
Вычислить 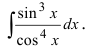
Решение:
Согласно изложенному способу вычисления, получим
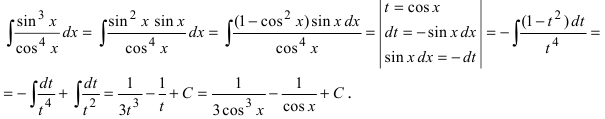
Пример:
Вычислить 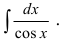
Решение:
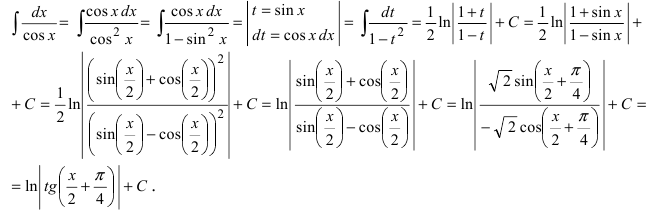
б). Если m и n являются четными неотрицательными целыми числами, то используют тригонометрические формулы понижения степени: 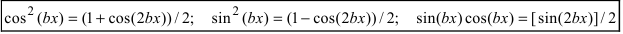 формулы подобия, например,
формулы подобия, например, 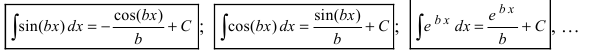
Пример:
Вычислить 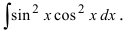
Решение:
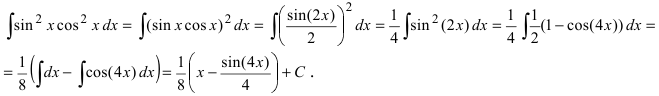
3. Интегралы вида 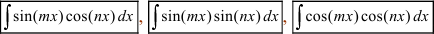 .
.
При вычислении таких интегралов используют формулы:
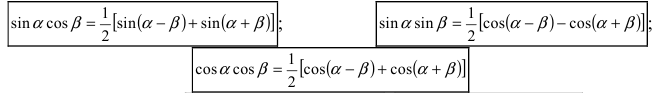
и формулы подобия:
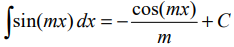 и
и 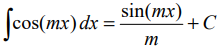
Пример:
Вычислить 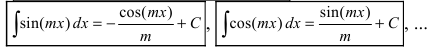
Решение:
Так как 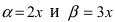 (обратите внимание на тот факт, что величина
(обратите внимание на тот факт, что величина 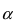 всегда определяется по синусу при наличии косинуса), то
всегда определяется по синусу при наличии косинуса), то 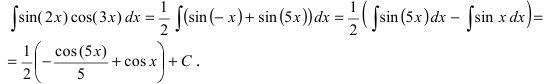
Пример:
Вычислить 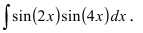
Решение:
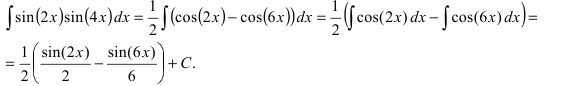
Интегралы вида  и
и  .
.
(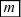 и
и  - целые положительные числа). Напомним, что
- целые положительные числа). Напомним, что 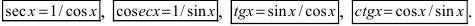 При интегрировании используются формулы
При интегрировании используются формулы 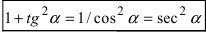 ,
, 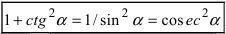 , при этом надо помнить, что
, при этом надо помнить, что 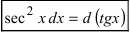 и
и 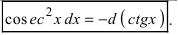
Пример:
Вычислить 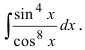
Решение:
Преобразуем подынтегральную функцию к виду
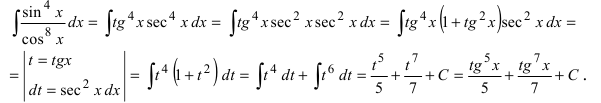
Частными случаями рассмотренных интегралов являются интегралы вида 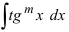 и
и 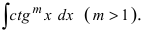 Такие интегралы вычисляются путем отделения квадрата подынтегральной функции и использованием вышеприведенных формул.
Такие интегралы вычисляются путем отделения квадрата подынтегральной функции и использованием вышеприведенных формул.
Пример:
Вычислить 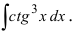
Решение:
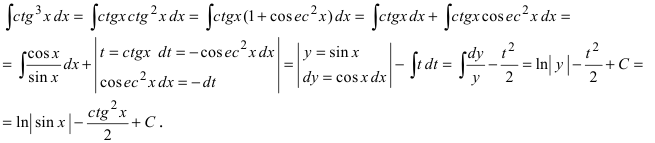
Интегралы вида 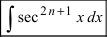 и
и 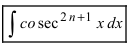
(n- целое положительное число).
Такие интегралы вычисляются по частям с использованием рекуррентных формул. Вычислим, например,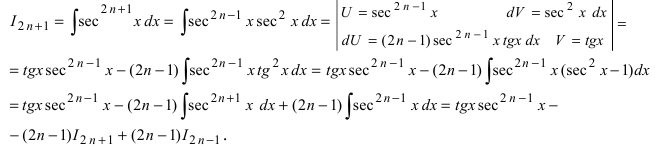
Решая это равенство относительно величины 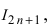 получаем
получаем
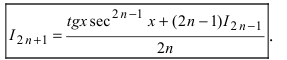
Определение: Соотношения полученного типа называются рекуррентными. Рекуррентные соотношения позволяют по известному значению более низкого порядка вычислять значения искомой величины более высокого порядка. Аналогично полученному рекуррентному соотношению получают формулу для вычисления 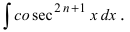
Пример:
Вычислить 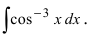
Решение:
Согласно рекуррентному соотношению получаем:
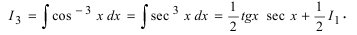
Интеграл 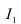 вычислен в п. 2а), поэтому окончательный ответ имеет вид
вычислен в п. 2а), поэтому окончательный ответ имеет вид
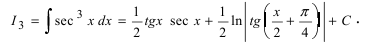
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Интегрирование тригонометрических выражений
- Интегрирование иррациональных функций
- Прямоугольная система координат на плоскости и ее применение
- Линии второго порядка
- Дифференциальное исчисление
- Исследование функций с помощью производных
- Формула Тейлора и ее применение
- Интегрирование рациональных дробей