Имеются выборочные данные о распределении вкладчиков по размеру вклада в Сбербанке города. Размер вклада

		Математическая статистика
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16472
		Прошла проверку преподавателем МГУ
		245 руб.

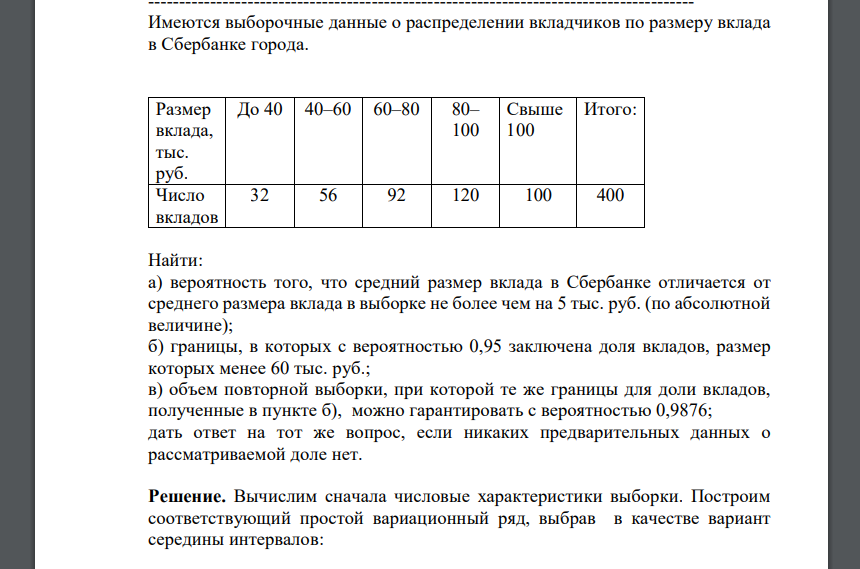
Имеются выборочные данные о распределении вкладчиков по размеру вклада в Сбербанке города. Размер вклада, тыс. руб. До 40 40–60 60–80 80– 100 Свыше 100 Итого: Число вкладов 32 56 92 120 100 400 Найти: а) вероятность того, что средний размер вклада в Сбербанке отличается от среднего размера вклада в выборке не более чем на 5 тыс. руб. (по абсолютной величине); б) границы, в которых с вероятностью 0,95 заключена доля вкладов, размер которых менее 60 тыс. руб.; в) объем повторной выборки, при которой те же границы для доли вкладов, полученные в пункте б), можно гарантировать с вероятностью 0,9876; дать ответ на тот же вопрос, если никаких предварительных данных о рассматриваемой доле нет.

Решение.

Вычислим сначала числовые характеристики выборки. Построим соответствующий простой вариационный ряд, выбрав в качестве вариант середины интервалов: Итого Найдем среднее:  Найдем исправленную дисперсию: . Найдем исправленное среднеквадратичное отклонение:  . Расчеты в таблице ниже:  Сумма а) Найдем вероятность того, что средний размер вклада в Сбербанке отличается от среднего размера вклада в выборке не более чем на 5 тыс. руб. (по абсолютной величине), то есть что предельная ошибка выборки равна 5.  Вероятность 0,99994 или 99,994%. б) Найдем границы, в которых с вероятностью 0,95 заключена доля вкладов, размер которых менее 60 тыс. руб. Выборочная доля вкладов, размер которых менее 60 тыс. руб. равна . Предельная ошибка для доли (1 ) Коэффициент  Получаем:  Тогда границы для доли всех вкладов размером менее 60 тыс. руб. имеют вид:  всех вкладов. в) Найдем объем выборки, при которой те же границы для доли вкладов, полученные в пункте б), можно гарантировать с вероятностью 0,9876. Нужно найти объем выборки n , при котором предельная ошибка будет также равна  w Формула для объема выборки имеет вид:  Коэффициент  Подставляем все данные:  Дадим ответ на тот же вопрос, если никаких предварительных данных о рассматриваемой доле нет. Тогда рекомендуется брать w  0,5 . Получаем: