Мультипроцессоры (Некоторые этапы из истории освоения массового параллелизма)

Содержание:

ВВЕДЕНИЕ

Компьютерное моделирование и постановка численных экспериментов являются важнейшими инструментами исследования наноструктурных объектов в различных отраслях научного знания и в наукоёмких технологических разработках. Не пытаясь описать всю литературу по этой тематике, сошлемся только на обзоры, опубликованные в журнале «Наноструктуры. Математическая физика и моделирование» по компьютерному моделированию в биологии [1], по проблемам параллельного программирования [2], по проблемам создания и функционирования баз данных [3] и другим направлениям развития и применения вычислительных средств [4], [5], [6].

В данной работе делается попытка анализа глубокого перелома в эволюции компьютерных систем, который медленно обозначался не одно десятилетие и сейчас проявился с полной определённостью. Сегодня можно утверждать, что главным направлением развития вычислительных средств на ближайшую перспективу станет освоение массового динамического параллелизма.

Массовый параллелизм это не 5, не 10 и даже не 100 процессоров, а сотни тысяч и миллионы процессорных элементов, работающих одновременно, согласованно и взаимосвязанно. В этих условиях синхронный подход к программированию, предполагающий опережающую разметку трассы процесса по каждой ветви, становится бессмысленным и неосуществимым. Массовый параллелизм может быть только динамическим, то есть возникающим оперативно шаг за шагом в ходе текущего осуществления вычислительных операций. При реализации динамического параллелизма вычислительный процесс должен сам прокладывать свой путь в аппаратной среде и быть способным эффективно заполнять высокопараллельный аппаратный ресурс.

Ситуация, открывающая принципиально новый этап развития вычислительных средств, определяется текущим состоянием технологии микроэлектронного производства. Выделим три принципиальные позиции, характеризующие современное состояние технологии.

Позиция первая: рост тактовой частоты остановлен и зафиксирован на уровне 2,2 ГГц. В предыдущие годы были достигнуты значения тактовой частоты на уровне 5,5 ГГц, но при этом получен неприемлемый рост энергозатрат. Технологи приняли решение вернуться к оптимальному значению 2,2 ГГц и более тактовую частоту не наращивать. Это означало необходимость пересмотра «закона Мура», в соответствии с которым технологи обязаны обеспечивать удвоение производительности кристалла каждые 18 месяцев.

Прогнозируемый рост числа транзисторов на кристалле носит линейный характер и пока не встречает ограничений. Отсюда следует вторая принципиальная позиция: устойчивый рост числа транзисторов позволяет переформатировать «закона Мура» и декларировать удвоение числа ядер на кристалле через каждые 18 месяцев (или каждые 24 месяца). На текущий момент в производстве достигнуты значения 2688 ядер на одном кристалле, выпускаемом компанией NVIDIA [7] и прогнозируется их дальнейший рост. Это и есть факт технологического оформления коренного перелома в развитии вычислительных средств. Освоение массового параллелизма становится основным инструментом обеспечения устойчивого роста производительности кристаллов. Отсюда неумолимо следует необходимость обновления технологии программирования. Неоднократно разными специалистами высказывалось мнение о том, что «теперь программирование придётся изобретать заново» [8]. Это очень показательное заявление, обозначающее смену вектора развития. Предшествующий этап развития вычислительных средств характеризовался ограничениями разработок в области архитектуры и организации вычислений. Проблема состояла в том, что в мире был наработан огромный задел программных продуктов, оцениваемый в сотни миллиардов долларов. Основным условием развития вычислительных средств было обеспечение преемственности и прямой переносимости программных продуктов и технологий, наработанных ранее. Теперь давление этого фактора заметно снижается, компьютерное сообщество объявляет о готовности к пересмотру и обновлению архитектурных концепций.

И, наконец, третья позиция. При повышении тактовой частоты энергозатраты растут как квадрат частоты. Передовые массивно-параллельные системы потребляют мегаватты энергии. Стоимость энергии начинает превышать стоимость оборудования. Энергопотребление ограничивает будущий рост мультипроцессорных систем. Поэтому актуально введение нового понятия вычислительной эффективности - performance/watt вместо пиковой производительности. Этим показателем активно пользуется компания Intel при описании своей продукции. В упрощённом виде это величина отношения числа операций на 1 ватт потребляемой энергии. Специалисты компании SUN предложили ввести более сложный критерий энергоэффективности SWaP (Space, Watts and Performance). Эта тема активно обсуждается, например, в [9].

Введение критерия энергоэффективности кристалла косвенно связано с числом транзисторов и означает явно сформулированное требование эффективного использования основного ресурса кристалла, который и определяется числом транзисторов. Теперь разработчики архитектуры должны ответить на вопрос – каково соотношение затрат транзисторов на обработку данных в арифметико-логическом блоке и на управление в других блоках процессора. Показатель степени интеграции в современных технологиях достиг порядка миллиарда транзисторов на кристалле и далее будет расти [10]. Однако каким бы не было велико число транзисторов и сколь бы ничтожна мала не оказалась их стоимость, разработчикам архитектуры отныне приходится отвечать за показатель энергоэффективности кристалла, а это требует рационально распределять транзисторный ресурс при проектировании.

Таким образом, можно констатировать, что сложились условия, критерии и объективные оценки, стимулирующие проведение фундаментальных разработок в области архитектуры перспективных вычислительных средств, которые должны решить следующие три проблемы:

- обеспечить реализацию массового параллелизма;

- обеспечить высокую эффективность организации вычислительных процессов по критерию числа операций, приведенных к энергозатратам:

- создать предпосылки для разработки принципиально новых технологий программирования.

ГЛАВА 1 ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ МУЛЬТИПРОЦЕССОРОВ И ИХ ИСПОЛЬЗОВАНИЯ

1.1 Некоторые этапы из истории освоения массового параллелизма

История освоения параллелизма полна разочарований и непрогнозируемых проявлений побочных и скрытых эффектов. Первичные ожидания устойчивого монотонного роста производительности в широком диапазоне значений числа обрабатывающих элементов в общем случае не подтвердились. Определённые положительные результаты получены только в случаях узкой специализации параллельных структур на определённый вид параллелизма, на определённый класс задач или на одну конкретную задачу.

С самого начала было понятно, что возможности распараллеливания вычислений в первую очередь ограничиваются свойствами решаемой задачи. Если в задаче выделяется 10 параллельных ветвей, наращивание числа обрабатывающих процессоров свыше десяти становится бессмысленным. График роста производительности системы в режиме решения данной задачи достигнет своего максимума при 10 процессорах и деле расти не будет. Более полно факт зависимости роста производительности от свойств задачи сформулировал Джин Амдал ещё в 1967 году [11]. В законе Амдала вводится основная характеристика параллельной системы в виде коэффициента ускорения , который определяется как отношение времени выполнения задачи на одном процессоре ко времени выполнения этой задачи на параллельной системе из процессоров . Поскольку   величина относительная, можно считать, что в числителе равно единице. Для определения временной баланс разбивается на две составляющие – последовательную, которая не поддаётся распараллеливанию и обозначается как доля от общего объёма вычислений , и параллельную, обозначаемую как . Доля поддаётся распараллеливанию и с ростом числа процессоров уменьшается, а доля остаётся неизменной.

Тогда ускорение может быть записано как соотношение:

Ниже на рис. 1 приводятся графики роста ускорения для разных вариантов соотношения параллельных и последовательных долей в задаче.

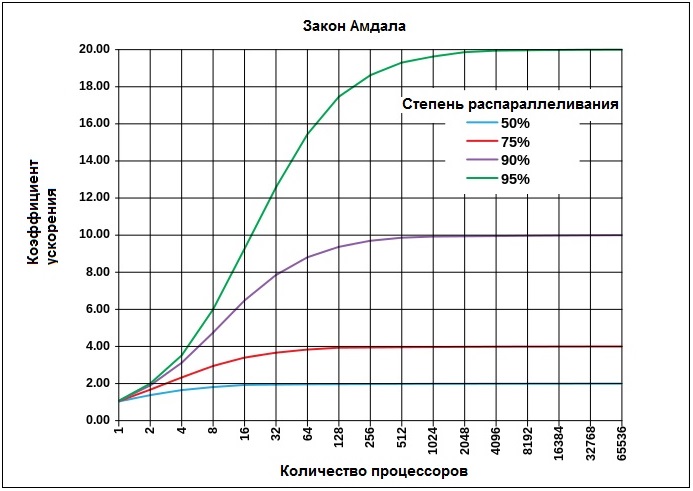
Рис. 1 Графики роста ускорения для разных вариантов соотношения параллельных и последовательных долей в задаче.

Закон Амдала наглядно иллюстрирует важный факт, говорящий о том, что каждая конкретная задача имеет определённый потенциал параллелизма и при исчерпании этого потенциала значение ускорения достигает своего предельного значения и далее не растёт при любом количестве процессорных элементов.

Закон Амдала даёт идеальную картину, в которой предполагается, что параллельная компонента задачи может дробиться и поглощаться параллельной структурой обработки неограниченно. В реальных условиях определение соотношения долей параллельных и последовательных компонент задачи, а также уровень дробления параллельной компоненты при распараллеливании зависят от архитектуры вычислительной среды, от методов программирования, размерности задачи и масштабов представления базовых фрагментов (так называемое мелкозернистое и крупнозернистое представление). В реальных условиях насыщение роста ускорения наступает раньше и при меньших значениях.

Движение в сторону максимального использования массового параллелизма предписывает выбирать крупноразмерные задачи и стремиться к их мелкозернистому представлению. А это в свою очередь создаёт значительные проблемы в области программирования, выбора архитектуры аппаратных средств и форм организации вычислений. Первые разработки высокопараллельных структур предпринимались в рамках классической фон Неймановской архитектуры, которая изначально предназначалась для построения сугубо последовательных синхронных форм функционирования. Попытка построения параллельной структуры как совокупности многочисленных последовательных синхронных ветвей, функционирующих параллельно, представляет собой сложную задачу с многочисленными проблемами и скрытыми побочными эффектами.

Значительным достижением в области построения параллельных систем была разработка в MIT архитектуры потока данных, известной как архитектура Data Flow. Первые публикации по архитектуре Data Flow относятся к середине 70-х [12]. Особенностью данной архитектуры является отсутствие понятия «последовательность инструкций», отсутствие счётчика команд и даже адресуемой памяти в привычном нам смысле. Программа в потоковой системе — это не набор команд, а вычислительный граф. Каждый узел графа представляют собой оператор или набор операторов, а ветви отражают зависимости узлов по данным. Очередной узел начинает выполняться, как только доступны все его входные данные. В этом состоит один из основных принципов Data Flow: исполнение инструкций по готовности данных.

Параллельно и независимо от проекта Data Flow и одновременно с ним велись работы по непроцедурным стилям программирования и в частности по функциональным языкам программирования [13]. Работы по функциональным языкам привели к необходимости разработки специальных машин, поддерживающих функциональные языки. Один из проектов завершился созданием макетного образца продукционной машины ELIZE [14].

Экспериментальная версия редукционной машины ELIZE представляет собой открытый набор стандартных фон Неймановских процессорных элементов с локальной памятью и объединённых общей шиной. Физическая реализация осуществлена на одноплатных транспьютерах промышленного производства. (Транспьютер - это классический процессор с локальной памятью и четырьмя портами для связи со смежными процессорами. По замыслу разработчиков на транспьютерных элементах предполагалось строить масштабируемые матричные структуры). При построении макетного образца редукционной машины применялся метод эмуляции, при котором требуемый набор нестандартных функциональных элементов создаётся путём программирования стандартных классических процессоров. Набор процессорных элементов позволяет распараллелить редукционный процесс, а по мере появления нередуцируемых символов, обозначающих атомарные функции, запускается процесс их исполнения на тех же процессорах.

Самое поверхностное знакомство с механикой работы машины потока данных и редукционной машины наталкивает на мысль о том, что проблема программирования архитектуры потока данных может быть решена средствами редукционной машины, интерпретирующей функциональные языки. При обеспечении совместимости правил построения функциональных записей и стандартов построения Data Flow пакетов результаты работы редукционной машины в части реализации редукционного процесса можно воспринимать как генерацию потокового графа для машины потока данных. Именно эта мысль получила серьёзное обоснование в известном докладе Бэкуса. В 1977 году был опубликован доклад Бэкуса, прочитанный им по поводу вручения премии Тьюринга [16]. Доклад содержит глубокий критический анализ фон Неймановской архитектуры и убедительно показывает исчерпание её возможностей. Во второй части доклада излагается программа развития вычислительных средств на ближайшее будущее, в основу которой положен тезис об объединении двух направлений разработок – проектов Data Flow и функциональных языков. И, наконец, третья часть доклада посвящена изложению основ функционального языка. В соответствии с программой Бэкуса работы по перспективным технологиям программирования должны быть сосредоточены вокруг разработки функциональных языков, а в части построения аппаратных средств с массовым параллелизмом необходимо принять за основу проект Data Flow.

Приведем на обозрение единственный известный нам проект в соответствии с программой Бэкуса в конце 80-х годов. Проект назывался редукционно-потоковая машина, основные сведения по проекту содержатся в патенте [17]. Программа разработки моделей и постановки модельных экспериментов была успешно выполнена. Структура моделей и основные результаты моделирования изложены в [18]. Представим на рис. 2 кривые роста коэффициента ускорения , который представляет собой отношение времени выполнения задачи на одном процессоре к времени выполнения задачи в многопроцессорной системе. При этом временные затраты оценивались в числе квантов модельного времени.

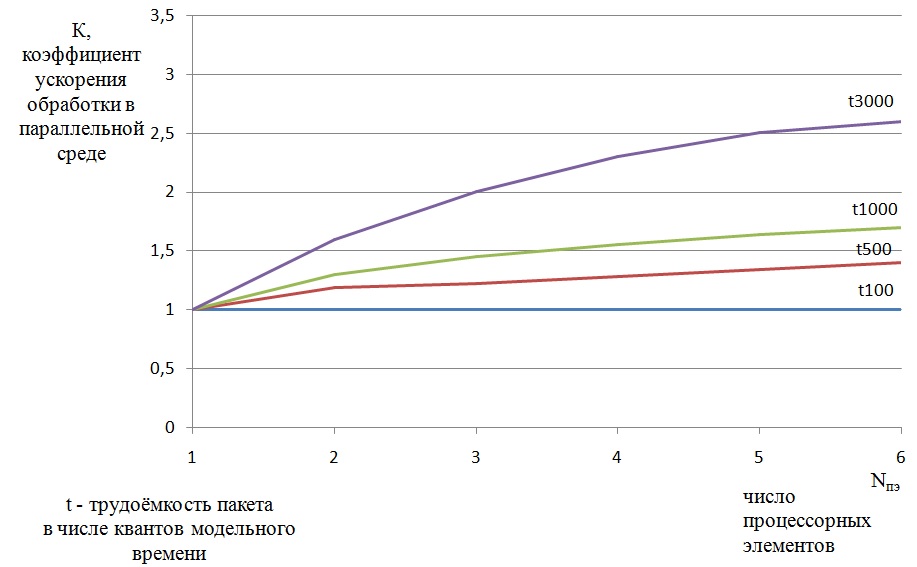
Рис. 2 Зависимость коэффициента ускорения от числа каналов обработки при разных значениях средней трудоёмкости пакетов

Главным выводом этого эксперимента явилось то, что реальные значения коэффициента ускорения оказываются неприемлемо низкими, а график роста входит в насыщение при относительно малом значении параллелизма – при 6 каналах обработки. Модель была построена для 16 каналов и в этом диапазоне показателя параллелизма коэффициент ускорения вышел на уровень 2,8 и далее не менялся. Полученные результаты моделирования означали приговор всему проекту. Поставленная цель – освоение массового динамического параллелизма средствами данного проекта не могла быть достигнута.

1.2 Результаты измерений производительности при выполнении алгоритмов БПФ

Проблема быстрой остановки роста производительности при наращивании степени параллелизма никуда не делась и со временем проявилась на макроуровне при эксплуатации кластеров и суперкомпьютеров. В этой связи целесообразно рассмотреть данные, полученные пользователями многопроцессорных систем в ходе исследования эффективности параллельного выполнения алгоритмов трёхмерного быстрого преобразования Фурье (3D БПФ), изложенные в [19]. Отметим, что существуют многочисленные версии специальных многопроцессорных систем, ориентированных на параллельное выполнение алгоритмов БПФ. Эти специализированные системы эффективно выполняют только один алгоритм – БПФ, другими алгоритмами их, как правило, не загружают. В тоже время алгоритмы БПФ являются наиболее проблемными при загрузке в универсальные параллельные системы. Именно алгоритмы БПФ характеризуются большими объёмами перекрёстных пересылок данных, в переходах, связывающих параллельные слои в общем графе алгоритма.

Приведём данные измерений временных затрат и вычисленные показатели ускорения в виде графиков из [19] и прокомментируем их.

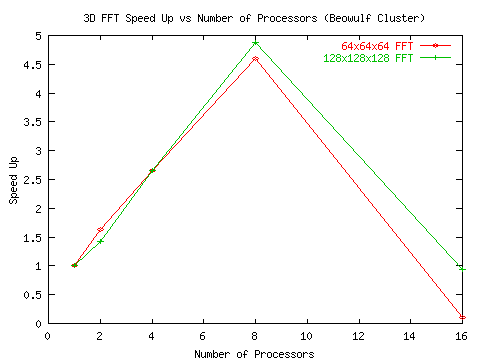
Рис. 3 Ускорения, полученные при прогоне алгоритмов 3D БПФ на установке Beowulf Cluster

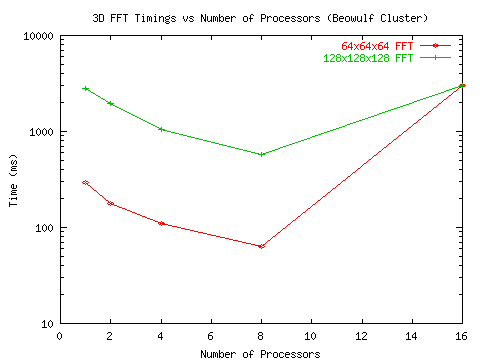
Рис. 4 Временные затраты при прогоне алгоритмов 3D БПФ

на установке Beowulf Cluster

Временные затраты получены в результате измерений, ускорения вычислены. В прогоне участвовали два варианта решения задачи - с размерностью 64х64х64 и с размерностью 128х128х128. Установка Beowulf Cluster это примитивный кластер, созданный на базе набора персональных компьютеров, объединённых средствами локальной офисной сети.

Вторая серия экспериментов выполнялась на установке Beowulf Cluster с более мощным коммутатором и более скоростной шиной. Результаты проведены на рис. 5 и рис. 6.

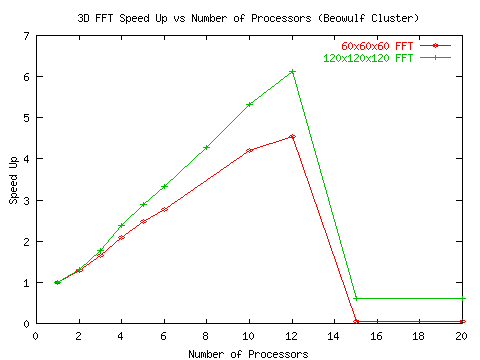
Рис.5 Ускорения, полученные при прогоне алгоритмов 3D БПФ

на улучшенной установке Beowulf Cluster

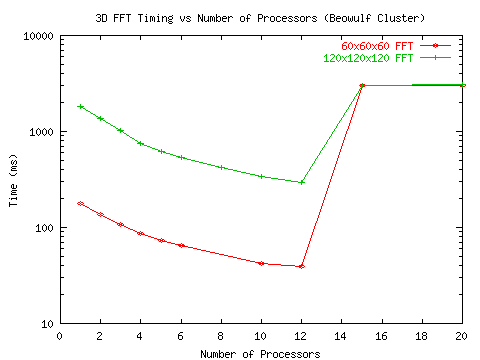
Рис. 6 Временные затраты при прогоне алгоритмов 3D БПФ

на улучшенной установке Beowulf Cluster

И наконец, авторы [19] получили доступ к более совершенной установке IBM SP2, построенной на базе скоростного коммутатора с развитой системой шин. Данные экспериментов приведены на рис.7 и рис 8.

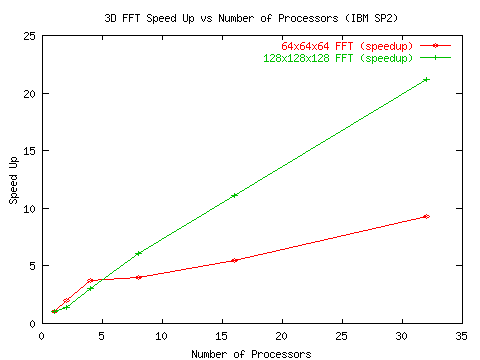
Рис. 7 Ускорения, полученные при прогоне алгоритмов 3D БПФ

на установке IBM SP2

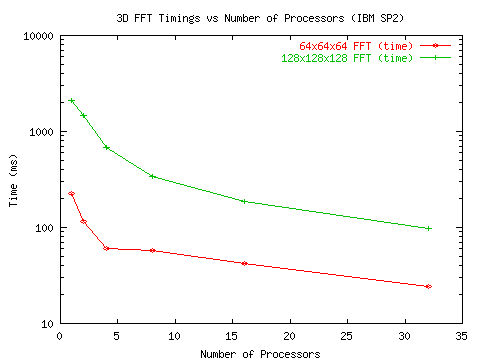
Рис. 8 Временные затраты при прогоне алгоритмов 3D БПФ

на установке IBM SP2

Приведенная последовательность графиков показывает, что при прогоне алгоритмов с высоким потенциалом параллелизма коэффициенты ускорения довольно низкие и после прохождения пика резко падают. Ситуация заметно улучшается по мере улучшения обменной среды, поддерживающей межпроцессорные передачи.

Схожие результаты на рис. 9 получили авторы статьи [20] в рамках реализации алгоритма Radix-4 БПФ на суперкомпьютере К-100 ИПМ РАН.

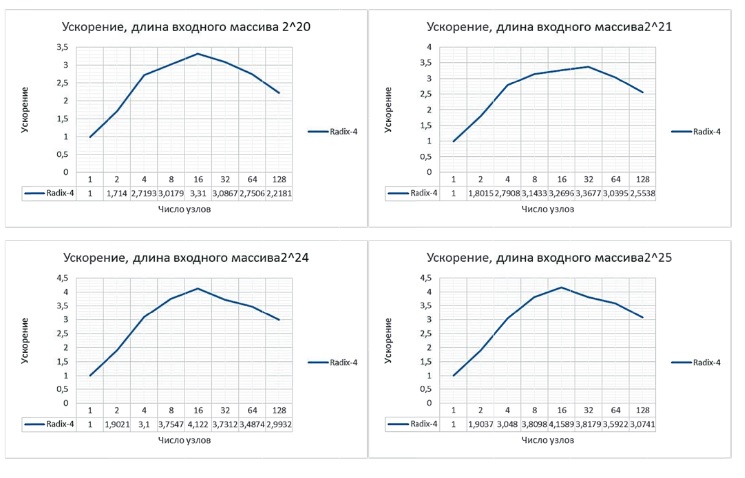
Рис. 9 Графики ускорений, полученных при вычислении алгоритма БПФ с различной длиной входного массива на кластере К-100

Как видно из графиков, максимальное ускорение не достигало 5, а на большом числе узлов, как и в работе [19], наблюдается спад.

1.3 Анализ факторов, ограничивающих рост производительности параллельных систем

Подведём итог. Рассмотрены ситуации роста производительности в двух достаточно разных средах – в классической многопроцессорной системе с общей шиной и в перспективном проекте неклассической архитектуры с элементами Data Flow. При этом результаты экспериментов похожие, если не сказать подобные. В случае с редукционно-потоковой машиной рассматривался результат модельного эксперимента, в случае с классической структурой получены данные измерений натурного эксперимента. В обоих случаях ход графиков роста коэффициента ускорения очень похож на графики, иллюстрирующие проявления закона Амдала. Однако надо сразу отметить, что наблюдаемый нами эффект быстрого прекращения роста производительности к закону Амдала не имеет никакого отношения, поскольку в обоих случаях насыщение наступает задолго до исчерпания потенциала параллелизма задачи. Мы имеем дело с другим явлением, природу и физический смысл которого предстоит выяснить.

Построим модель распределения временных затрат при параллельных вычислениях на конкретном примере реализации алгоритма быстрого преобразования Фурье (БПФ). На рис. 10 приведен граф процесса вычисления алгоритма 16-точечного БПФ. В данном случае размерность БПФ выбрана по соображениям наглядности и удобства визуального восприятия рисунка. Нам необходимо проиллюстрировать топологическую природу графа, представляющего регулярную сетку с определённым принципом построения. Далее известно, что граф процесса вычисления алгоритма БПФ легко масштабируется на любую размерность по степеням двойки.

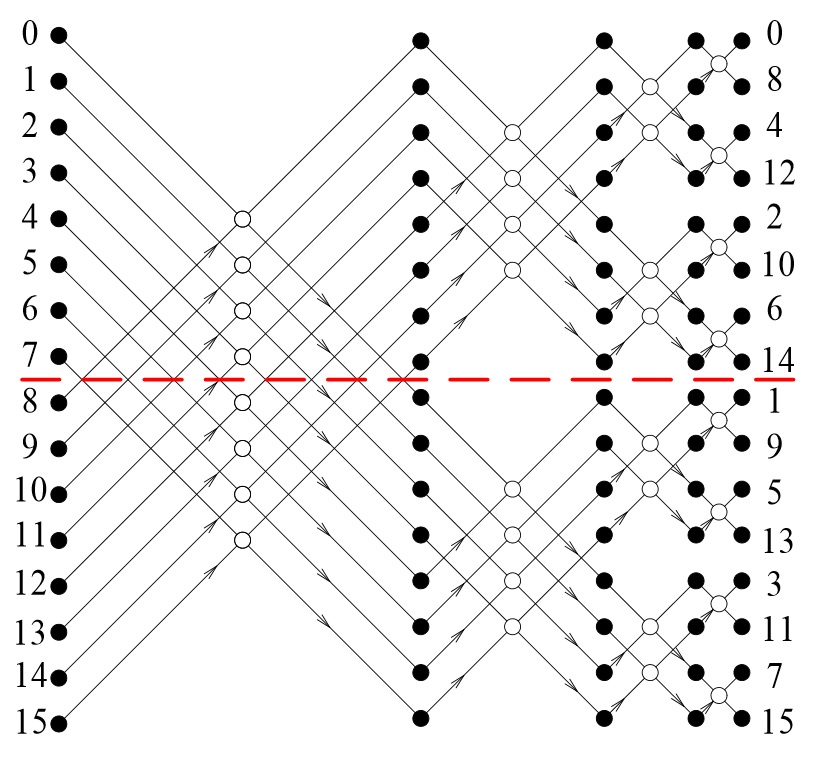
Рис. 10 Граф процесса вычисления 16-точечного БПФ

Сплошными кружочками на рисунке обозначены комплексные операнды, записанные в алгебраической форме, каждый из которых представляются парой действительных коэффициентов. Нумерация операндов в левой части рисунка отображает порядок следования отсчётов во входной сигнальной последовательности. На выходе происходит перестановка порядка следования отсчётов, это побочный эффект данного алгоритма. Контурные кружочки обозначают базовую процедуру с двумя входами и двумя выходами, называемую бабочкой БПФ. Базовая процедура представляет собой алгоритм решения системы четырёх алгебраических уравнений. На выходе базовой процедуры порождается пара комплексных чисел, каждое из которых представлено парой действительных коэффициентов. Намеренно опустим целый ряд деталей с целью установления основных свойств графа вычисления БПФ; для нас важно, что граф носит регулярный характер. На рис. 10 видно, что структура графа разбивается на ряд вертикальных слоёв, представленных одним числом вычислительных процедур. Вся структура графа заполнена одной базовой вычислительной процедурой, которая принимает на входе и порождает на выходе одни и те же форматы данных. Параллелизм обработки данных осуществляется в пределах слоя, слои образуют последовательность, при переходах между слоями осуществляется обмен данными. Фазы параллельной обработки и фазы обменов данными идентичны по всему графу, что позволяет корректно провести подсчёт временных затрат на осуществление вычислительных и обменных операций.

Размерность алгоритма наращивается по степеням двойки и если число входных отсчётов равно , то число слоёв в графе равно , а число вычислительных процедур в слое равно . Соответственно общее число процедур в графе равно . Основные показатели структуры графа, необходимые для вычисления производительности параллельного представления процесса масштабируются, что позволяет нам воспользоваться наглядностью графического представления 16-точечного БПФ и далее пересчитать требуемые характеристики для любой другой размерности. Для 16-точечного БПФ имеем следующие показатели число слоёв в графе равно 4, число базовых процедур в слое равно 8, всего процедур в графе 32. Задача состоит в том, что бы построить модель вычисления коэффициента ускорения, в которой в явном виде учитываются время вычисления базовых процедур и время передачи данных между процессорами при переходах с текущего слоя на следующий. При этом мы определяем время обмена данными как сумму времени передачи данных и времени выполнения протокольных событий, обеспечивающих доступ к обменной среде.

Определим ускорение как отношение времени выполнения алгоритма на одном процессоре ко времени выполнения алгоритма на процессорах , где размерность алгоритма, а - число процессоров. Поскольку искомое ускорение есть величина относительная для данной модели мы будем оценивать времена выполнения определённых действий в условных микротактах работы оборудования. Примем, что время выполнения базовой операции равно 10 микротактам. Тогда время выполнения 16-точечного БПФ на одном процессоре будет состоять только из времени выполнения базовых операций, поскольку обмен данными при этом отсутствует.

Числитель будет состоять из трёх членов, зависящих от числа процессоров n . Время вычисления базовых процедур будет равно . Или в общем виде

Для определения времени пересылки данных необходимо рассмотреть структуру графа на рис. 10. При двух процессорах граф будет рассечен на две части по горизонтальному направлению как это отмечено пунктирной линией и две его половины будут загружены в разные процессоры. В этом случае обмен данными произойдёт только при переходе с первого на второй слой. При этом в каждом из двух процессоров будет вычисляться по 4 бабочки и каждая из них будет располагать только половиной входных данных, а вторую половину данных необходимо будет получить из другого процессора. Следовательно, обмен будет состоять из двух сеансов передач, содержащих по 4 отсчёта. Общий объём пересылаемых данных составит отсчётов.

При 4-х процессорах верхняя и нижняя половинки графа рассекаются аналогичным образом. В этом случае появляется необходимость обмена данными при переходе со второго на третий слой, объём пересылаемых данных по прежнему равен отсчётов, а суммарный объём составит . Для 8 процессоров каждая выделенная по горизонтали часть графа вновь рассекается на две и мы получаем параллельное представление всего графа, состоящее из восьми последовательных нитей, каждая из которых содержит последовательность из трёх базовых операций. При этом появляется необходимость обменов при переходе со второго на третий слой с тем же объёмом передаваемых данных. Общий объём обменов будет равен . отсчётов. Таким образом, в общем случае число передаваемых отсчётов будет равно .

Протокольные события в обменной среде сопровождают сеансы связи и в упрощённой ситуации их подсчёт можно осуществить как некоторое фиксированное время, выраженное в условных микротактах и привязанное к сеансу связи. По мере наращивания числа процессоров происходит увеличение числа сеансов и уменьшение объёмов данных, передаваемых в каждом сеансе. При двух процессорах происходит один обмен па переходе от первого слоя ко второму, который состоит из 2 сеансов – от первого процессора ко второму и от второго к первому. При четырёх процессорах имеет место 2 обмена, в каждом из которых осуществляется по 4 сеанса и общее число сеансов равно 4 + 4. При восьми процессорах происходит три обмена и в каждом из них по 8 сеансов, всего 8 + 8 + 8. Таким образом, в общем случае число сеансов может быть определено как .

Посчитаем общие затраты времени при 2 процессорах. Время вычисления сократится вдвое и составит условных микротактов.

Время передачи данных учитывается как объём передаваемых данных приведенный к пропускной способности шины. При двух процессорах осуществляется передача восьми отсчётов по два слова в каждом, что равно 16 словам. По определению мы принимаем производительность шины равную передаче 1 слова за один микротакт, следовательно, искомое время обмена данными составит 16 условных микротактов.

Временные затраты на осуществление протокольных событий вычисляется как затраты на один протокол умноженные на число сеансов. Примем по определению, что на один протокол затрачивается 5 условных микротактов. Для данного случая, осуществления одного обмена, состоящего из двух сеансов, это составит .

Таким образом, суммарные временные затраты на вычисление 16-точечного БПФ В нашей модели при двух процессорных элементах составляют 186 условных микротактов, а коэффициент ускорения = 1,72. Аналогично проводится подсчёт для 4 и 8 процессоров. Данные сведены в Таблицу 1.

Таблица 1 – Свод данных

Число процессоров	1	2	4	8
Время вычисления (условные микротакты)	320	160	80	40
Время пересылки данных (условные микротакты)		16	32	48
Время выполнения протокола (условные микротакты)		10	40	120
Суммарное время (условные микротакты)	320	186	152	208
Коэффициент ускорения	1	1,72	2,11	1,54

График роста коэффициента ускорения для 16-точечного БПФ представлен на рис. 11. Приведенная модель в целом поддерживает динамику роста коэффициента ускорения, качественно совпадающую с результатами наблюдений и модельных экспериментов, описанных ранее.

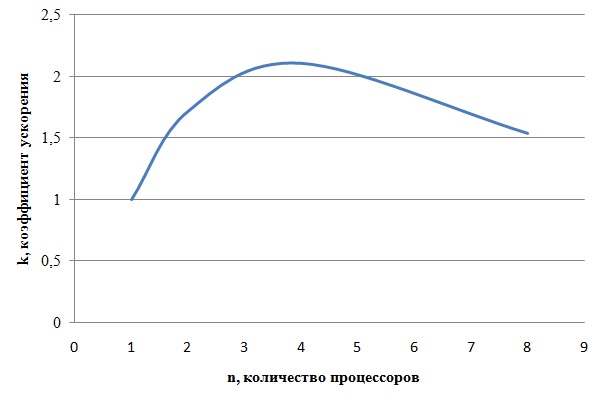
Рис. 11 График роста коэффициента ускорения для 16-точечного БПФ

Модель может быть аппроксимирована на любую размерность алгоритма БПФ. Общая формула для подсчёта времени выполнения алгоритма приводится ниже.

Первое слагаемое - это соотношение для времени выполнения вычислений, которое учитывает время счёта базовой операции и число базовых операций в алгоритме равное .

Второе слагаемое это время, затраченное на передачи данных между процессорами. Здесь объём передаваемых данных, выраженный в машинных словах, делится на величину , пропускную способность шины, которая в данном случае принимается равной 1, что означает передачу одного слова за один микротакт.

Третье слагаемое это затраты на осуществление протокольных мероприятий, обеспечивающих доступ к шине для совершения сеанса передачи данных. Параметр задаёт время выполнения протокола для одного сеанса. В данном примере мы определяем его значение равным 5 условным микротактам. Общее время затрат на протоколы вычисляется умножением на число сеансов, равное .

В качестве демонстрационного примера мы выбираем Результаты вычислений коэффициента ускорения для алгоритма БПФ на 1024 отсчёта. Граф алгоритма при данной размерности состоит из 10 слоёв по 512 бабочек в каждом слое, всего в графе содержится 5120 базовых процедур. Максимальный потенциал распараллеливания данного алгоритма составляет 512 последовательных линий из 10 базовых процедур каждая. Результаты вычислений для = 1024 при = 1 и = 5 приведены в Таблице 2

Таблица 2 – Сводная таблица

число процессоров	1	2	4	8	16	32	64	128	256	512
время выполнения (условные микротакты)	51200	26634	14888	9592	7616	7520	8864	12048	18632	32356
коэффициент ускорения	1	1,92	3,44	5,34	6,72	6,81	5,78	4,25	2,75	1,58

График роста коэффициента ускорения приводится на рис. 12

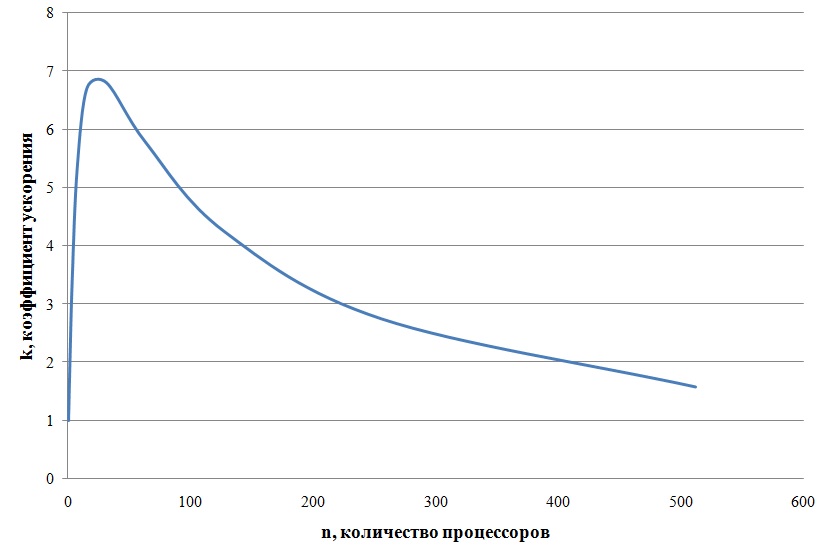
Рис. 12 График роста коэффициента ускорения для БПФ на 1024 точки

Данная модель позволяет исследовать поведение всех обозначенных компонентов, формирующих баланс временных затрат и их зависимость от числа процессоров. На рис.13 приводится динамика времени выполнения алгоритма по всем слагаемым: времени счёта, времени пересылки данных и времени протоколов доступа к обменной среде.

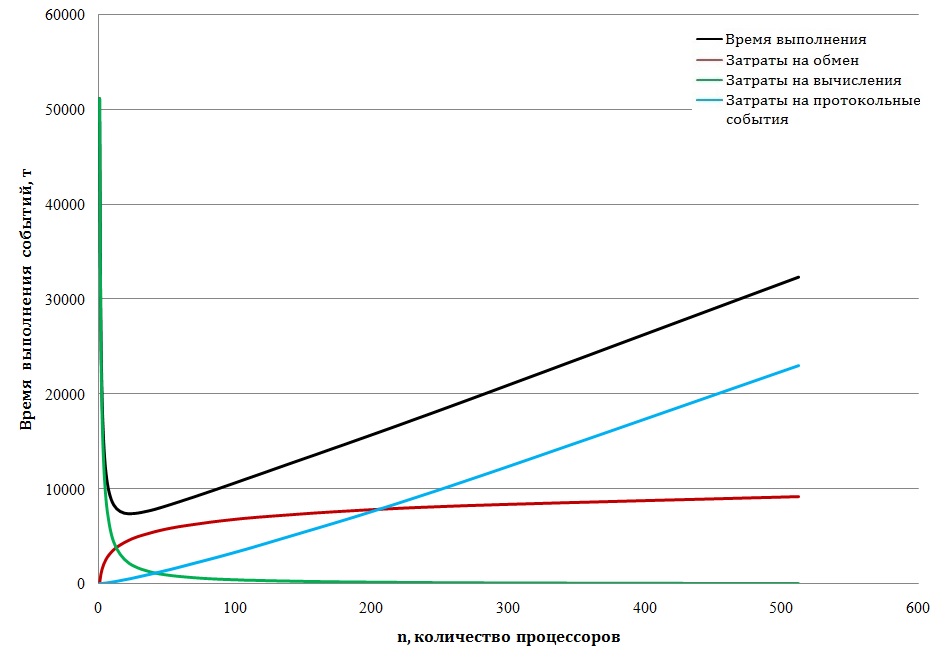
Рис. 13 Динамика времени выполнения алгоритма по основным слагаемым

Приведенный график показывает полную картину во всём диапазоне значений числа процессорных элементов и временных затрат. В дополнение к общей картине на рис. 14 в увеличенном масштабе изображён начальный фрагмент динамики роста временных затрат.

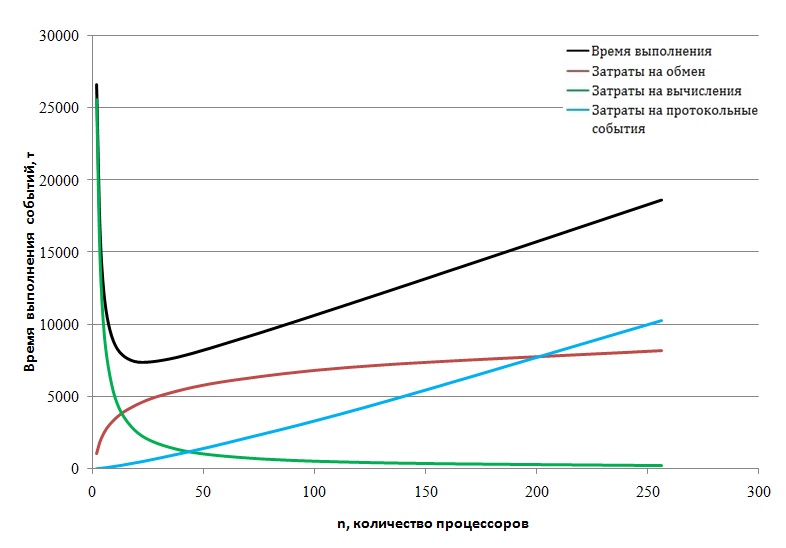
Рис. 14 Начальный фрагмент динамики времени выполнения алгоритма по основным составляющим

Подведём итог - алгоритм имеет потенциал параллелизма, позволяющий распределить на 512 процессорах 512 последовательных линий, каждая из которых представляет собой последовательность из 10 базовых процедур. Следовательно, в идеальном случае можно получить коэффициент ускорения близкий к значению 512. Полученное на модели значение ускорения 6,81 , заметно отличается от ожидаемых 512. Модель позволяет обнаружить в явном виде причины такого расхождения. Время счёта устойчиво падает с ростом числа процессоров , но его вклад в рост ускорения подавляется двумя слагаемыми, которые растут с ростом . Это временные затраты на обмен данными и на выполнение протокольных событий. Обе растущие компоненты порождаются работой обменной среды и событиями, обслуживающими параллелизм.

Обменная среда является самой консервативной составляющей аппаратного обеспечения. Идея общей шины значительно упрощает структуру аппаратных средств, но в целом является инерционным звеном, снижающим показатели производительности вычислительных средств. Сделанные нами вычисления показывают неприемлемость применения общей шины при построении многопроцессорных систем с массовым параллелизмом.

Далее мы рассмотрим улучшенный вариант применения общей шины. Допустим, что многоядерная структура формируется путём наращивания кластеров, состоящих из 16 процессоров, объединённых общей шиной. Это позволяет распараллелить обменные операции, локализованные в пределах кластера. При этом обмены между кластерами осуществляются по общей шине верхнего уровня, которая объединяет кластеры. Для модельных подсчётов сохраним ранее принятые параметры. Рассматривается граф алгоритма БПФ, = 1024 при параметрах шины = 1 и = 5, что означает передачу одного машинного слова за один такт и осуществление протокола доступа к шине за 5 тактов. Обмены между процессорами внутри кластера осуществляются одним проходом по шине кластера. Доступ процессора к обмену между кластерами требуют двух проходов по шинам. Сначала проход по кластерной шине для выхода на межкластерную шину и далее проход по этой шине в смежный кластер.

Время вычислений будет устойчиво снижаться с ростом , а время выполнения обменов и протоколов будет рассчитываться по двум разным принципам. Общее время обменов в распараллеленной ветви будет делиться на число кластеров. В ветвях осуществления межкластерных обменов при суммировании будет учитываться факт двойного прохода по разным шинам. Результаты вычислений сведены в Таблицу 3.

процессоры	1	2	4	8	16	32	64	128	256	512
Вычисление	51200	25600	12800	6400	3200	1600	800	400	200	100
Передача	0	1024	2048	3072	4096	4096	5120	6656	8346	10368
Протокол	0	10	40	120	320	640	1600	4160	10560	25820
Сумма	51200	26634	14888	9592	7616	6336	7521	11216	19106	36288
Ускорение на 1 шине	1	1,92	3,44	5,34	6,72	6,81	5,78	4,25	2,75	1,58
Ускорение на многошинной структуре	1	1,92	3,44	5,34	6,72	8,08	6,8	4,56	2,68	1,4

Таблица 3

На рис. 15 изображены кривые роста ускорения. Красным цветом отмечено ускорение в структуре с одной шиной, синим в системе с множеством шин.

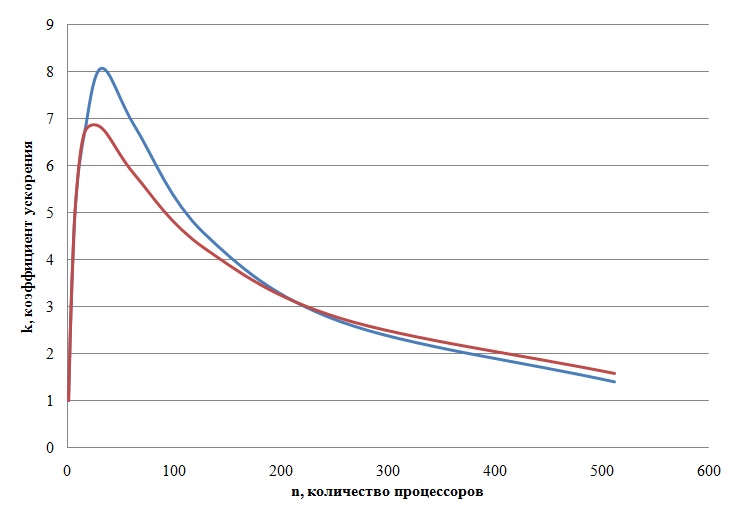
Рис. 15 Кривые роста ускорения. Красная линия для одной шины, синяя для множества шин

На графике видно, что улучшение более чем скромное, переломить ситуацию быстрого насыщения роста производительности не удаётся. На рис. 16 приводится семейство кривых изображающих поведение отдельных компонентов процесса.

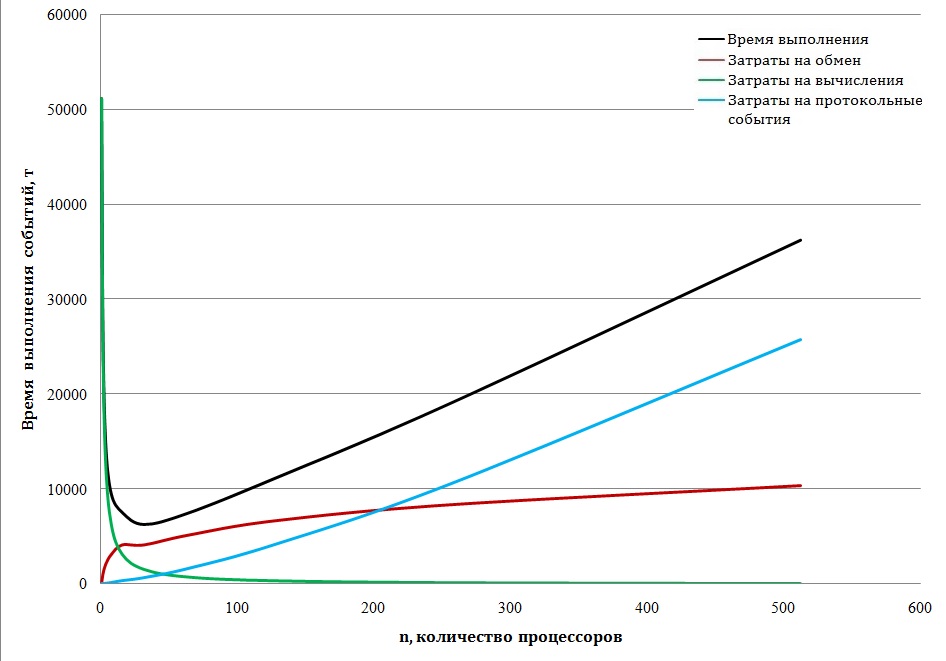
Рис. 16 Динамика роста временных затрат по основным компонентам процесса

Красная линия, отражающая рост затрат на осуществление обменов данными в начальной фазе демонстрирует попытку сформировать тенденцию к снижению затрат, но далее растущий параллелизм подавляет эту тенденцию.

Данные модельного эксперимента показывают, что структура с множеством шин может дать определённое улучшение на относительно небольших значениях параллелизма, в пределах нескольких десятков. Далее по мере роста числа процессоров в область сотен экземпляров результаты многошинной структуры сравниваются с результатами одной шины. Таким образом, мы можем объяснить заметное улучшение результатов, полученных в [19] . В последнем эксперименте вычисления проводились на более совершенной установке IBM SP2 с более скоростной многошинной обменной средой.

На рис. 16 видно, что время, затраченное на пересылки данных растёт умеренно и при больших значениях параллелизма роль этой компоненты стабилизируется. Наиболее агрессивной компонентой, определяющей быстрый рост временных затрат при больших значениях параллелизма является время выполнения протокольных событий. Дело в том, что с ростом числа процессоров обмен данными дробится на множество мелких порций, каждая из которых оформляется как самостоятельный сеанс передачи, требующий доступа к шине. Таким образом число протоколов разрастается и их удельный вес в обменных операциях становится подавляющим.

Следует учесть, что в нашей модели приняты допущения о некой идеальной ситуации абсолютной доступности шины. В реальности при коллективном использовании шины происходят конфликты доступа, при которых запускаются процедуры шинного арбитража и ожидания в очереди. Фактическая ситуация значительно хуже. Ценность данной модели в том, что она позволяет выявить основные причины подавления роста производительности на качественном уровне.

ГЛАВА 2 ПРАКТИЧЕСКИЕ АСПЕКТЫ ПРИМЕНЕНИЯ МУЛЬТИПРОЦЕССОРОВ

2.1 Обзор работ по коммутационным средам

На текущий момент среди обменных сред (сетей интерконнекта) выделяются 4 основных класса, основанных, преимущественно, на топологии сети: сеть с коллективно используемой средой, сеть с прямым доступом, сеть с косвенным доступом и гибридная сеть. В сетях с коллективно используемой средой обменная среда делится между всеми коммутирующими устройствами. В таких сетях одновременно только одно ядро может использовать сеть. Сеть обычно является пассивной, поскольку она не генерирует сообщения. По причине ограниченной пропускной способности такие сети не могут быть использованы в суперкомпьютерах. Ярким представителем такой сети является сеть с топологией толстое дерево (Fat Tree).

Альтернативой такого подхода является наличие прямых связей от точки к точке, непосредственно соединяющих ядра с подмножеством смежных ядер в сети. В таком случае, любая связь между не близлежащими устройствами требует передачи информации через несколько промежуточных ядер. Такие сети называются сетями с непосредственным доступом.

Важным параметром применимости сетей для суперкомпьютеров является их масштабируемость. Каждое ядро представляет собой программируемый компьютер с собственным процессором, локальной памятью и прочими поддерживающими устройствами. Такие ядра могут иметь различные функциональные возможности. Например, подмножество ядер может содержать векторные процессоры, графические процессоры и процессоры ввода/вывода. Общим компонентом ядер является роутер, который поддерживает передачу сообщения от ядра к ядру. По этой причине сети с прямым доступом так же можно назвать сетями, основанными на роутерах. Каждый роутер имеет непосредственное соединение с соседними роутерами. Обычно, роутеры соединены парой ненаправленных каналов в разных направлениях. Хотя, функции роутера могут быть представлены локальным процессором, выделенные роутеры используются в мультикомпьютерах с высокой производительностью, позволяя перекрывать вычисления и коммуникацию каждого ядра. С увеличением числа ядер в системе так же растет общая ширина коммуникации, пропускная способность памяти и возможности обработки системы. Таким образом, сети с прямым доступом являются популярной архитектурой межсоединений для создания крупномасштабных параллельных компьютеров. [21]

Каждый роутер поддерживает некоторое число входящих и исходящих каналов. Внутренние каналы или порты соединяются с локальным процессором/памятью роутера. Кроме того, часто обеспечивается только одна пара внутренних каналов, некоторые системы используют большее число внутренних каналов с целью избежать коммуникационного бутылочного горлышка между локальным процессором/памятью и роутером [22]. Внешние каналы используются для коммуникации между роутерами. Сеть с непосредственным доступом определяется при соединении входящих каналов одного ядра с исходящими каналами других ядер. Два ядра, соединенных напрямую называются соседними. Каналом называют внешний канал. Часто каждое ядро имеет фиксированное число входных и выходных каналов, и каждый входной канал имеет соответствующую пару в виде выходного канала. Имеется больше число способов соединения таких каналов. Очевидно, что каждый узел сети должен быть доступен из любого другого узла сети.[21]

В отличие от непосредственно соединенных сетей, в косвенных сетях для соединения ядер применяется один или несколько переключателей. В случае если имеется несколько переключателей, они непосредственно соединяются между собой. Тогда, при передаче информации от ядра к ядру требуется проход информации через несколько переключателей. И четвертая группа – гибридные сети.

Совершенствование коммутационных сред является одним из главных направлений развития суперкомпьютеров. Основным путем развития суперкомпьютеров является увеличение числа вычислительных элементов. Текущий уровень и скорость развития вычислительных элементов превосходит уровень и темпы развития обменных сред. Рассмотрим некоторые из них:

• Толстое дерево (Fat Tree);
• Бабочка (Butterfly);
• Стрекоза (Dragonfly);
• Тор (Torus).

В больших суперкомпьютерах решающее значение для достижения максимальной производительности имеет сеть межсоединений. Маршрутизация – один из основных аспектов разработки межсоединительных сетей. Стратегия маршрутизации определяет путь каждого пакета, следующего между источником и точкой назначения. Маршрутизация является обусловленной (маршрутизация по закрепленному маршруту), если существует только один предопределенный путь для каждой пары источник - место назначения, или адаптивной, если доступно несколько путей для пакета. Алгоритмы обусловленной маршрутизации обычно обеспечивают очень низкую балансировку трафика в сети, но они гораздо проще для воплощения и обладают неблокируемыми маршрутами. Кроме того, для сетей, в которых важным является заказ сообщений между источником и назначением, обусловленная маршрутизация является простым способом гарантии доставки пакета надлежащим образом. С другой стороны, алгоритмы адаптивной маршрутизации принимают во внимание текущее состояние сети, и решение о маршрутизации пакета принимается на основе этих данных. Такая информация может включать состояние каналов или длину очереди на роутере. Адаптивная маршрутизация обычно лучше балансирует сетевой трафик, тем самым помогая сети получить более высокую пропускную способность за счет повышения стоимости маршрутизаторов.

Алгоритмы адаптивной маршрутизации часто превосходят по производительности алгоритмы с обусловленной маршрутизацией, но данное заявление не является истиной в случае топологий, основанных на толстом дереве. Применение каждого вида обменной среды определяется параметрами конкретной задачи: количество вычислительных ядер, наличие и тип коммутации между ними и т д.

Топология толстое дерево может быть использована только при относительно низком числе коммутируемых процессоров, т.к. с ростом числа этих процессоров усложняется система интерконнекта в геометрической прогрессии, необходимы сложные переключатели, которые будут обеспечивать доступ к данным из разных «ветвей» дерева. На рис. 17 представлена схема коммутации вычислительных элементов в топологии толстой дерево.

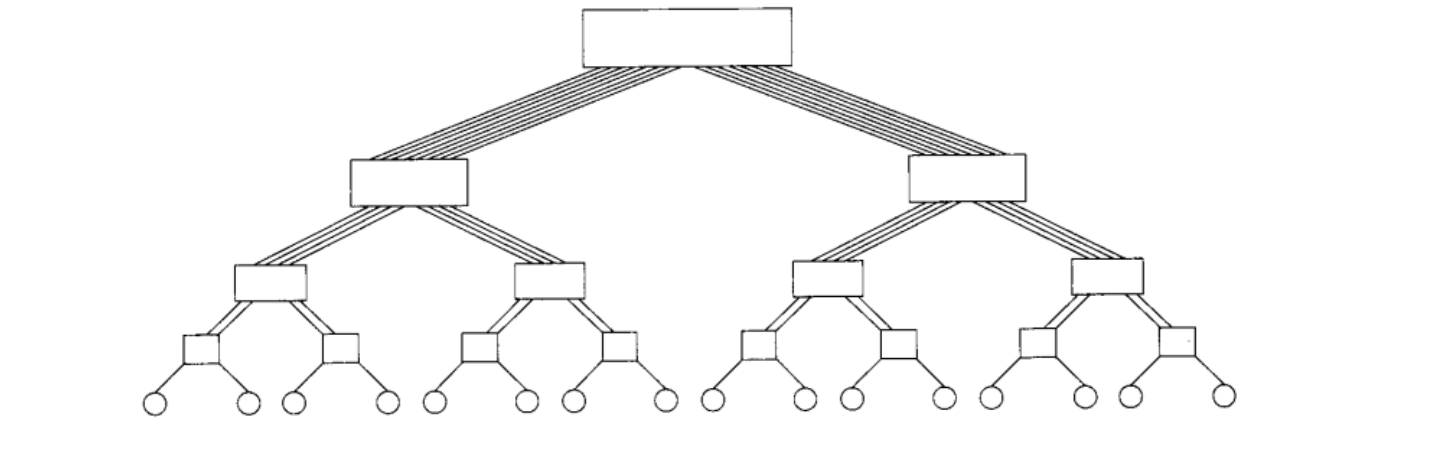
Рис. 17 Схема объединения узлов коммутаторами в топологии «толстое дерево».

Топология стрекоза была разработана для использования роутеров с большим числом разъемов и для согласования пределов корпусов / межсоединений высокомасштабных систем. Стрекоза – трехуровневая сеть, которая согласует три уровня иерархии корпусирования. Как показано на рис. 18, на низшем уровне каждый роутер соединен с Р выводами сети. Такие соединения обычно выполняются посредством объединяющей РСВ платы. На втором уровне группы роутеров объединяются локальную сеть. Эти соединения выполняются посредством электрических соединений средней длины с использованием корпусов или небольших групп корпусов. В этой работе мы рассматриваем, прежде всего, топологию стрекоза, где локальная сеть является законченным соединением (одномерная сплюснутая бабочка), где каждый роутер имеет (а-1) локальных соединений с другими роутерами в группе. Большие группы могут быть построены с использованием многомерных сплюснутых бабочек для локальной сети. На самом высоком уровне каждый роутер имеет h глобальных каналов, соединенных с другими группами с применением длинных оптических кабелей. Таким образом, порядок каждого роутера p+a+h-1, и каждая группа имеет a*h глобальных каналов. В сетях максимального размера с топологией типа стрекоза, один глобальный канал соединяется с каждой парой групп.

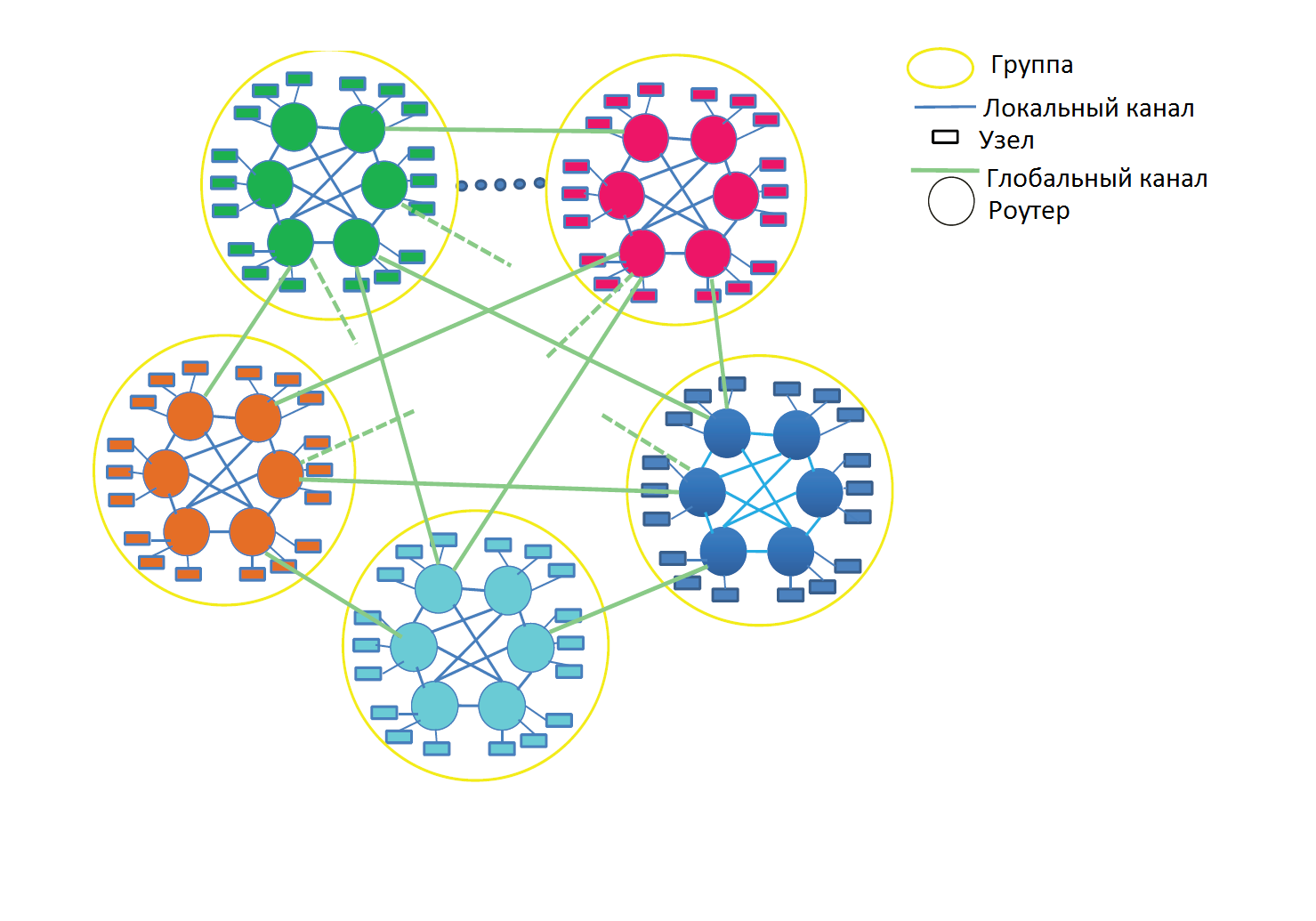
Рис. 18. – Схема объединения узлов коммутаторами в топологии «стрекоза»

Для "доброкачественного" трафика, который балансирует нагрузку на каналы сети, сеть с топологией стрекоза обладает наилучшей минимальной маршрутизацией. Минимальная маршрутизация проходит в три этапа. Сперва пакет маршрутизируется локально от исходящего вывода к глобальному каналу, следуя к группе назначения. Далее пакет передается по глобальному каналу. И в итоге пакет передается в группе назначения к заданному узлу. С минимальной маршрутизацией каждый пакет пересекает один глобальный канал и заданные локальные одномерные сети, всего - два локальных канала.

Сети интерконнекта с топологией «Тор» хорошо подходят для систем коммуникации сетей на чипе, архитектурах связи процессор-память и в коммуникационных сетях. Сеть с топологией тор является хорошо масштабируемой – число элементов сети можно нарастить с относительной легкостью (в сравнении с топологией толстое дерево, где с увеличением числа ядер значительно увеличивается число роутеров и, вместе с тем, сложность сети).[24]

На рис. 19 представлена классическая топология тора размерностью 4х4. В узлах сети находятся переключатели, которые имеют слоты, к которым могут быть подключены такие ресурсы, как процессор, блок памяти, пользовательское оборудование или какое-либо другое периферийное устройство. Предполагается, что переключатели имеют буферные устройства для контроля трафика в сети.[25]

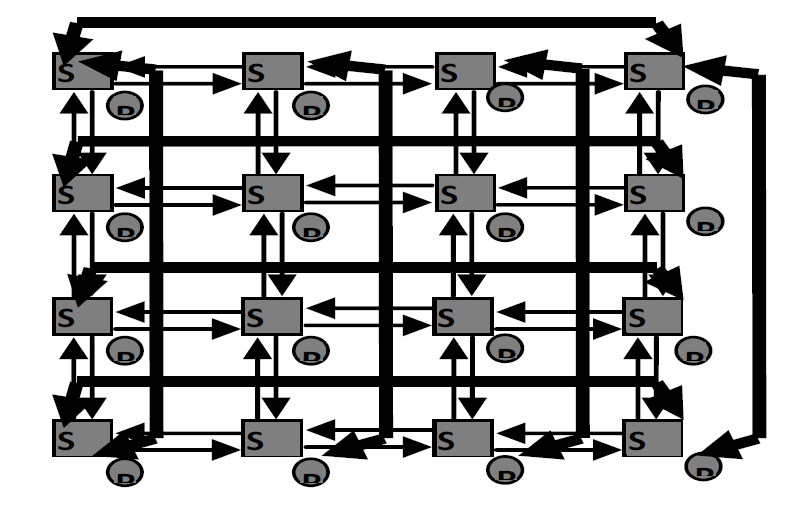
Рис. 19. Схема объединения узлов в сети «двумерный тор» размерностью 4х4.

Теперь же стоит привести сравнение стоимости сетей при различной реализации топологии. Сети интерконнекта встроены в иерархию корпусированных систем. На самом нижнем уровне роутеры соединяются посредством печатных плат, которые, в свою очередь, подключаются к объединительной плате. Одна или несколько таких соединительных плат устанавливаются в корпуса, которые объединяются между собой электрическими или оптическими кабелями для полного формирования системы. Основной составляющей в стоимости сети являются кабели, соединяющие стойки и передатчики, в разъемы которых подключаются такие кабели. [23]. Для снижения стоимости сети необходимо соответствие топологии с характеристиками доступных технологий интерконнекта.

Максимальная ширина полосы пропускания электрического кабеля падает с ростом длины, поскольку имеет место ослабление сигнала по причине линейного увеличения скин-эффекта и поглощения в диэлектрике с ростом длины [25]. Для типовых скоростей передачи сигналов высокой производительности (10-20 Гб/с) и технологических параметров, электрические токопроводящие дорожки ограничены длиной в 1м в печатных платах и 10м в кабелях. На больших дистанциях значительно уменьшается скорость передачи, и становится необходимым встраивание повторителей сигнала, что сказывается на стоимости сети.

Исторически высокая стоимость оптических кабелей ограничивает их применение на очень длинных расстояниях или приложений, требующих высокой производительности вне зависимости от стоимости реализации. На рис. 20 представлено сравнение стоимости активных оптических кабелей Intel Connects Cables [26] и электрических кабелей с повторителями[27].

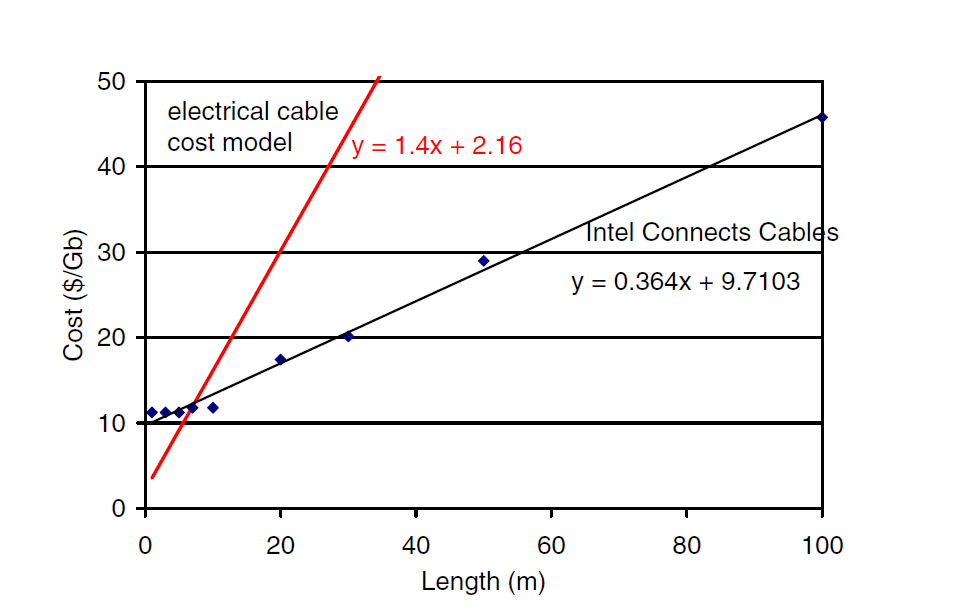
Рис. 20 Сравнение стоимости электрических кабелей с повторителями и активных оптических кабелей в зависимости от длины кабеля.

Из рисунка видно, что оптические кабели имеют более высокую первоначальную стоимость, но более низкую стоимость за единицу длины. Основываясь на представленных данных, точка пересечения лежит на длине кабеля порядка 10 метров. Для расстояний ниже 10м целесообразно использование электрических кабелей, для расстояния выше 10 м – оптических.

Топология уплощенная бабочка сокращает стоимость сети путем неиспользования промежуточных роутеров и каналов. В результате, стоимость топологии плоская бабочка сокращается примерно на 50% в сравнении с топологией Клос [28] при сбалансированном трафике. Топология стрекоза расширяет топологию плоская бабочка путем увеличения эффективности разъемов роутера для дальнейшего сокращения стоимости и увеличения масштабируемости сети.

Для сетей с топологией стрекоза и плоская бабочка и количеством разъемов до 1000 все роутеры соединены и топологии являются идентичными по количеству роутеров и стоимости. Для полностью соединенных топологий нет выигрыша в стоимости при попытке использования виртуального роутера, т.к. это будет только повышать стоимость сети. Для больших сетей, стрекоза более масштабируема не только потому, что в таких сетях большее эффективное основание роутера, , но и размер группы в два раза больше размера для плоской бабочки, что ведет к более низкой стоимости. Для сетей с числом выводов <4000 стрекоза показывает снижение стоимости порядка 10% по причине снижения средней длины кабеля при тех же размерах в плоской бабочке. Для сетей с >4000 выводов стрекоза обеспечивает 20% снижение стоимости по сравнению с плоской бабочкой по причине более коротких глобальных кабелей.

Стоимость интерконнекта для 3D тора, как показано на рисунке, значительно превосходит стоимость для прочих топологий, поскольку требуется большое число кабелей для обеспечения высокого диаметра сети. Для сетей с 1000 ядер, стрекоза примерно на 62 % дешевле. Сокращение стоимости сети при топологии стрекоза так же трансформируется в сокращение потребляемой мощности как показано в [27].

2.2 Оценка эффективности реализации вычислений

Расположение точки насыщения роста производительности определяется соотношением временных затрат на полезную работу и на издержки разных видов. Естественным образом возникает вопрос – почему в рассмотренных примерах динамика роста производительности параллельных систем ограничивается столь низкими значениями коэффициентов ускорения и степени параллелизма. Это 3-х кратное ускорение при 6 процессорных элементах в примере с моделированием редукционно-потоковой архитектуры и 6-х кратное ускорение при 12 узлах обработки во втором примере? Если определяющим фактором являются соотношения временных затрат на полезную работу и на издержки необходимо провести оценку существующих форм организации вычислений с целью определения источников издержек и возможности их радикального сокращения. Необходимо учитывать, что при распараллеливании процессов издержки, свойственные одному процессорному элементу размножаются кратно показателю параллелизма. Кроме того, порождаются дополнительные издержки обслуживания параллелизма, которые прибавляются к общему грузу издержек и таким образом суммарные издержки растут опережающим темпом. В современных условиях, когда произошло введение критерия эффективности кристалла по показателю числа операций на единицу затрат энергии учет издержек и определение их соотношения к полезной работе кристалла становится критическим показателем, от которого зависит возможность реализации массового параллелизма.

Рассмотрим основные положения классической архитектуры с точки зрения оценки издержек и эффективности организации процессов. Стоит напомнить, что все промышленно выпускаемые в настоящее время вычислительные средства построены по классической архитектуре. Неклассические архитектуры существуют как проекты или модели и не переходят в стадию промышленной реализации. Сущность архитектурной идеи наиболее полно воплощается в знаковой системе, средствами которой осуществляется программирование машины и управление внутренними процессами.

В архитектуре классической машины фон Неймана управление вычислительными процессами осуществляет простейшая знаковая система, называемая линейный императивный язык. Элементами императивного языка являются команды, которые в совокупности образуют функционально полный набор базисных функций. Функциональная полнота базисного набора команд позволяет декларировать тезис алгоритмической универсальности машины - средствами системы команд можно запрограммировать любой алгоритм. Программа представляет собой линейную последовательность команд.

Основой аппаратной реализации знаковой системы является машинное слово – это битовая строка определённой длинны. Длина или разрядность машинного слова это одна из основных характеристик машины. В языке машины существует две версии интерпретации машинных слов – слова команды и слова операнды. Команда реализована на аппаратном уровне как битовая строка, разбитая на несколько битовых секций или полей, имеющих своё содержательное назначение. Далее для экспертной оценки эффективности организации процессов будем использовать некую гипотетическую машину с фиксированным трёхадресным форматом команды и с памятью, в которой осуществляется адресный доступ к машинным словам. Это не соответствует реальной организации современных машин. Так, например доступ в память осуществляется по байтам, что необходимо для поддержки переменных форматов команд и данных. Команды и данные размещаются в разных блоках памяти и читаются независимо по разным каналам доступа. И таких отличий от предлагаемой к рассмотрению гипотетической машины огромное число, но все эти отличия не меняют суть архитектурной идеи, а их учёт не только осложнит, но и сделает невозможной экспертную оценку эффективности организации вычислений.

Структура команды гипотетической машины приведена на рис. 21.

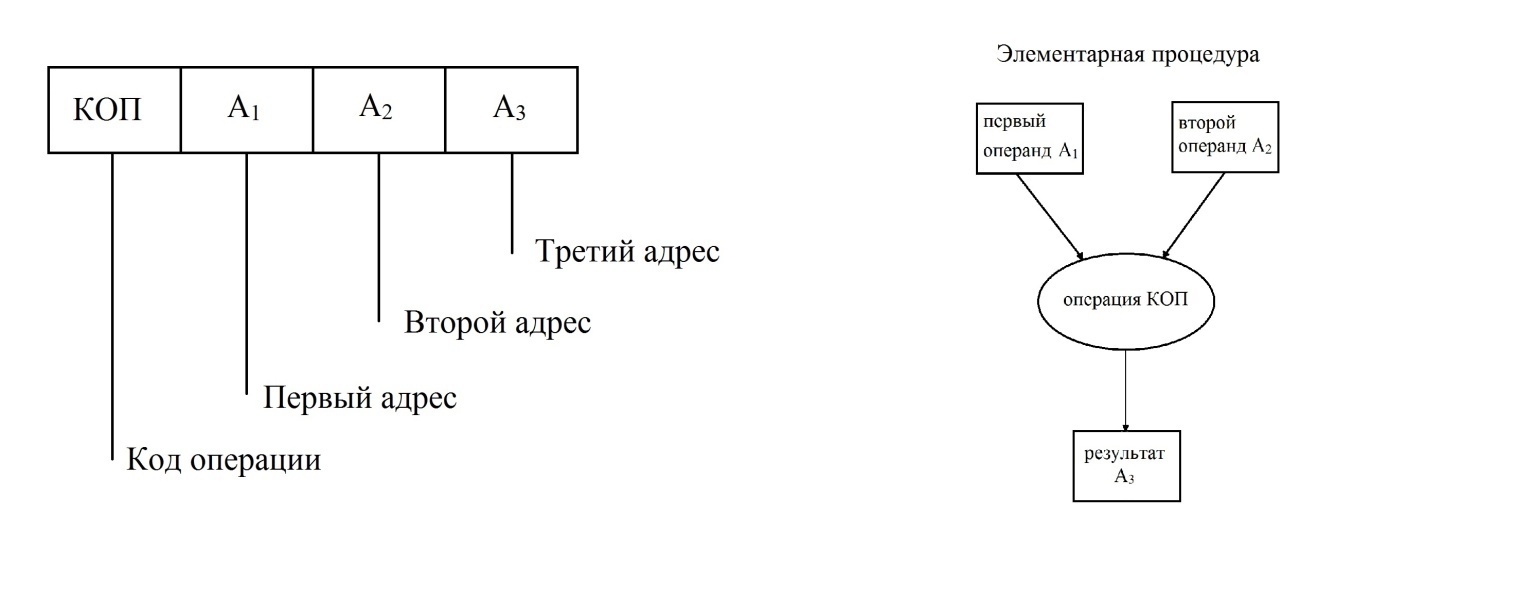
Рис. 21 Структура команды

Первое битовое поле кодирует операцию и называется КОП. КОП интерпретируется как число в двоичной системе и далее дешифрируется аппаратурой по таблице соответствия. Следующие три поля это так называемые адресные поля, которые обозначаются как А1, А2 и А3. Это числа в двоичной системе счисления, по которым осуществляется доступ в память. Память состоит из массива регистров, имеющих индивидуальные номера или адреса. В регистрах памяти размещаются машинные слова. По предъявлению адреса осуществляется доступ к заданному регистру для чтения либо записи. Содержательно команда представляет элементарную процедуру вычислительного процесса, поддерживающую бинарную операцию с двумя входными операндами и одним результатом. Так, например, А1 и А2 могут обозначать адреса, по которым в памяти размещаются два входных операнда, а А3 обозначает адрес для записи результата. Процессор связан с памятью каналом доступа, память служит местом размещения машинных слов. Память не различает слова как команды или операнды и это позволяет записывать в неё и программы и данные. Программист условно разделяет пространство памяти на сегменты для раздельного размещения программ и данных. Вычислительный процесс представляет собой поток обменов процессора с памятью, в котором циркулируют машинные слова, имеющие статус команд и операндов. Различение машинных слов на команды и операнды происходит при чтении. При этом команды читаются в устройство управления, а операнды в арифметико-логический блок.

Изложенное до сих пор позволяет зафиксировать одно очень важное следствие – знаковая система классической машины не является языком описания процессов вычисления и обработки данных. Язык машины является средством описания процессов преобразования состояний памяти. Команды, из которых состоит программа, привязаны не к данным, а к адресам памяти. Для того что бы процесс преобразования состояний памяти превратился в процесс обработки данных необходимо принять меры, обеспечивающие размещение нужных данных в нужных адресах памяти строго к тому моменту, когда соответствующая команда будет активирована и осуществит обращения к заданным адресам. Эти меры осуществляются как на аппаратном, так и на программном уровнях и являются основными источниками издержек и накладных потерь, сопровождающих вычислительный процесс. Для оценки эффективности организации процессов в гипотетической машине нам необходимо рассмотреть временную диаграмму и установить соотношение временных затрат на полезную работу и на сопутствующие обеспечивающие события, которые являются накладными потерями ресурса времени. В итоге нам необходимо оценить коэффициент полезного действия (КПД) машины как процентное соотношение разных работ на временной шкале.

Основным элементом временной диаграммы машины является такт выполнения команды, который состоит из следующих пяти микротактов: чтения команды, чтения первого операнда, чтения второго операнда, выполнения операции и записи результата. Сделаем допустимое в данном случае огрубление и будем считать, что все микротакты имеют равное время выполнения. Полезным квантом временной диаграммы считается только один микротакт – выполнение команды. Все остальные являются обеспечивающими и составляют накладные потери или издержки. Тогда получается, что на уровне выполнения одной команды языка машины во временной диаграмме полезный квант занимает 20%, а на издержки приходится 80%.

При построении простейшей процедуры некий стереотипный фрагмент программы повторяется многократно. Например, обрабатывается таблица, имеющая некоторое число атрибутов в строке и несколько сотен строк. Процедура состоит из программы обработки строки и цикла, повторяющего эту программу многократно по числу строк. Мы знаем, что адресные поля команды привязывают её к конкретным регистрам памяти. Это позволяет написать программу процедуры обработки строки таблицы. При повторном вызове процедуры программу обработки строки таблицы необходимо привязать уже к другим адресам, в которых размещается другая строка таблицы. При этом существует запрет на изменения в теле программы в ходе её выполнения. (В противном случае будет утерян принцип стереотипности и повторяемости программы). Проблема перемещаемости процедуры над данными решается через механизм косвенной адресации. При косвенной адресации в адресных полях команды не указывается непосредственный адрес размещения операнда, а указывается некий фиксированный в памяти регистр, в котором находится реальный адрес операнда. Далее по этому адресу осуществляется обращение в память за нужным операндом. При косвенной адресации для доступа к операнду необходимо осуществить два цикла обращения в память. Сначала обратиться в фиксированный регистр, извлечь, содержащийся в нём адрес и далее по этому адресу извлечь операнд. Известно, что время исполнения команды в основном определяется временем цикла обращения в память. Следовательно, полученные нами 20% КПД необходимо снизить вдвое до 10%. И это ещё не всё. Для реализации перемещаемости процедуры над данными необходимо перед началом каждого следующего прохода в цикле заменить адреса в фиксированных регистрах. Это осуществляется за счёт приращения адресов на некий фиксированный шаг. Таким образом, возникает целый пласт вычислительных работ, который называется адресная арифметика. Объёмы преобразований адресной арифметики равны объёмам основной обработки, поскольку необходимо модифицировать адреса всех операндов. Следовательно, КПД урезается ещё вдвое до 5%.

Из структуры команды, приведенной на рис. 21 следует, что возможности прямой адресации памяти из адресных полей команды весьма ограниченные. Если длина машинного слова равна 32 разрядам, каждое поле команды содержит по 8 разрядов. Это значит, что непосредственно из адресных полей команды можно адресовать не более чем 256 слов. По этой причине трёхадресный формат команды оказался проблемным и наибольшее распространение получил двухадресный формат, который позволяет при 32-х разрядном слове иметь два адресных поля по 12 разрядов и непосредственно адресовать 4096 слов. А это означает, что для реализации элементарной процедуры обработки в общем случае понадобится более одной команды, что только ухудшает временной баланс издержек. С учётом некоторой статистики применения коротких и длинных форматов команд мы вынуждены снизить КПД до 3%.

В современном компьютере адресное пространство оперативной памяти исчисляется гигабайтами. Дальнейшее расширение объёмов оперативной памяти стало возможным при осуществлении механизма многоступенчатой адресации. При ступенчатой адресации, например при двухступенчатой, пространство памяти расчленяется на страницы, регистры которых доступны из адресного поля команды. Страницам, в свою очередь, присваиваются свои адреса или номера страниц. Для реального доступа в память необходимо совместить адресное поле команды и номер страницы. При этом номер страницы представляет старшую группу разрядов, а адресное поле команды младшую группу разрядов реального адреса обращения в память. Номер страницы хранится в специальном индексном регистре в составе процессора. Это так называемый блок регистров общего назначения, сохраняющих вычислительную обстановку процессора и в частности его позиционирование в общем поле памяти. Назначение номера страницы и его занесение в индексный регистр осуществляет загрузчик, специальная системная программа низкого уровня, осуществляющая управление ресурсами памяти и обслуживающая загрузку приложения в память. Мы не станем здесь излагать детали этого достаточно громоздкого механизма, а только вынуждены будем констатировать, что осуществление перемещаемости приложения в памяти большого объёма и механизм многоступенчатой адресации урезают оценку КПД ещё наполовину до 1,5% .

При оценке эффективности организации вычислений, приведенной выше, мы ограничились рассмотрением уровня простейшей процедуры, погружённой в аппаратную среду. Это заведомо очень упрощённая ситуация. На самом деле необходимо понимать, что реальные условия работы компьютера осуществляются в системной среде, поддерживающей мультизадачные режимы. Выполнение системных функций и обработка прерываний ложатся на тот же единственный процессор и продолжают нагружать временную диаграмму. Так что в реальности эффективность функционирования современного классического компьютера по нашей экспертной оценке не превышает одного процента. В качестве метафоры можно утверждать, что на одно полезное действие приходится не менее сотни обеспечивающих, которые являются издержками принятых форм организации процессов.

Традиция проектирования аппаратных средств вычислительной техники складывалась в условиях подавляюще высокой стоимости аппаратуры. Поэтому издержки укладывались в последовательные ряды и выполнялись на одном оборудовании последовательно. По мере развития технологии микроэлектронного производства принцип экономии аппаратных затрат перестал быть доминирующим. Современные инженерные решения создают другую ситуацию, отличную от той на которой мы провели вышеприведенную экспертную оценку эффективности функционирования компьютера. Так, например, в современных процессорах программы и данные размещаются в разных блоках памяти, а выборки команд и данных осуществляются по разным каналам и совмещаются во времени, что заметно улучшает временную диаграмму. Текущие операнды подкачиваются порциями в сверхоперативную память и обеспечивают бесперебойную работу арифметического блока. И таких решений множество. Суть их сводится к тому, что издержки выносятся из последовательных рядов временной диаграммы и размещаются в дополнительной аппаратуре, которая работает параллельно с основной. Но главное заключается в том, что груз издержек остаётся прежним. Издержки не устраняются, а поглощаются дополнительной аппаратурой, а аппаратура это и есть основной ресурс кристалла, выраженный в числе транзисторов. Технология обеспечивает размещение миллиардов транзисторов на кристалле и есть две стратегии его заполнения. Можно сохранить примитивную структуру процессора с последовательным размещением издержек во времени и построить кристалл, содержащий 100 ядер. А можно усложнить процессор разгрузить его временную диаграмму и разместить издержки на дополнительной аппаратуре. Но тогда на кристалле будет размещаться не 100 низкоскоростных ядер, а 20 высокоскоростных. Суммарная пропускная способность кристалла останется прежней, поскольку определяющим является факт существования сотни обеспечивающих действий на одно полезное. Это константа, характеризующая архитектурную идею. Именно введение критерия эффективности по соотношению числа полезных действий на единицу затрат энергии позволяет осуществить объективную оценку эффективности инженерных решений. Вынос обеспечивающих действий из временной диаграммы и размещение их на дополнительной аппаратуре создаёт иллюзию повышения эффективности при условии, что стоимость транзисторов ничтожна. Но энергию эти действия потребляют при любом размещении и при разных инженерных решениях никуда не деваются. Выделенные нами при экспертной оценке накладные потери являются следствием архитектурной идеи и порождаемых ею форм организации процессов. Инженерные ухищрения не устраняют издержки, а манипулируют их размещением, и только вновь введенный критерий энергоэффективности кристалла позволит запустить тенденцию к критической оценке и пересмотру архитектурной концепции.

Начинать работы по созданию высокопараллельных структур с таким грузом издержек и такой низкой эффективностью организации процессов, по меньшей мере проблематично, а по результатам, рассмотренных нами в первой части статьи примеров, бесперспективно. При распараллеливании издержки тиражируются кратно степени параллелизма. Но при этом неизбежно возникают новые специфические издержки на обслуживание параллелизма. Мероприятия по организации параллельной работы множества процессорных элементов несут в себе тот же порок низкоэффективных форм организации процессов. Т.е. при обслуживании параллелизма вновь генерируются десятки и сотни накладных расходных событий на единицы полезных. Поэтому при решении целого ряда актуальных задач с высоким потенциалом параллелизма насыщение роста производительности наступает практически сразу при 10 – 15 процессорах и значениях 3-х, 4-х кратного ускорения. Параллелизм блокируется низкоэффективными формами организации вычислительных процессов. Факт существования эффекта насыщения не является фатальным. Точку насыщения можно перемещать и в перспективе обеспечивать реализацию высоких значений параллелизма. Фатальной является крайне низкая эффективность организации процессов в классической архитектуре.

Существует ли альтернативные решения, позволяющие строить вычислительные системы с более высокими показателями эффективности организации вычислительных процессов? Имеются ли приемлемые решения в области разработки неклассических архитектур? Наиболее значительным событием в этом направлении было создание архитектуры потока данных, известной как архитектура Data Flow. Первые публикации по архитектуре потока данных [11] [12] были восприняты с большим энтузиазмом. Машина потока данных действительно представляет собой принципиально новый архитектурный проект, поскольку язык машины потока данных существенно отличается от линейного императивного языка машины фон Неймана. Перечислим эти отличия. Язык классической машины описывает программу как линейную последовательность команд. Команда представляет фиксированную элементарную процедуру вычислительного процесса. Адресные поля команды ссылаются не на данные, а на адреса регистров памяти. Команды исполняются в порядке их следования в записи программы. Здесь следует вновь напомнить, что внутренний язык классической машины не является языком описания вычислительных процессов, он описывает процессы изменения состояний памяти. Подгон процедур изменения состояний памяти к вычислительному процессу есть основное содержание работы программиста, но это содержание не фиксируется средствами языка машины. Это есть источник некорректности технологии программирования классических машин. А главный порок классической архитектуры это антагонизм последовательной записи процесса с его параллельной и асинхронной природой.

Опишем подробнее основные положения архитектуры Data Flow. Язык машины потока данных существенно отличается от языка классической машины по всем перечисленным позициям. Основной лексической единицей языка машины потока данных является пакет. Структура пакета приведена на рис. 22.

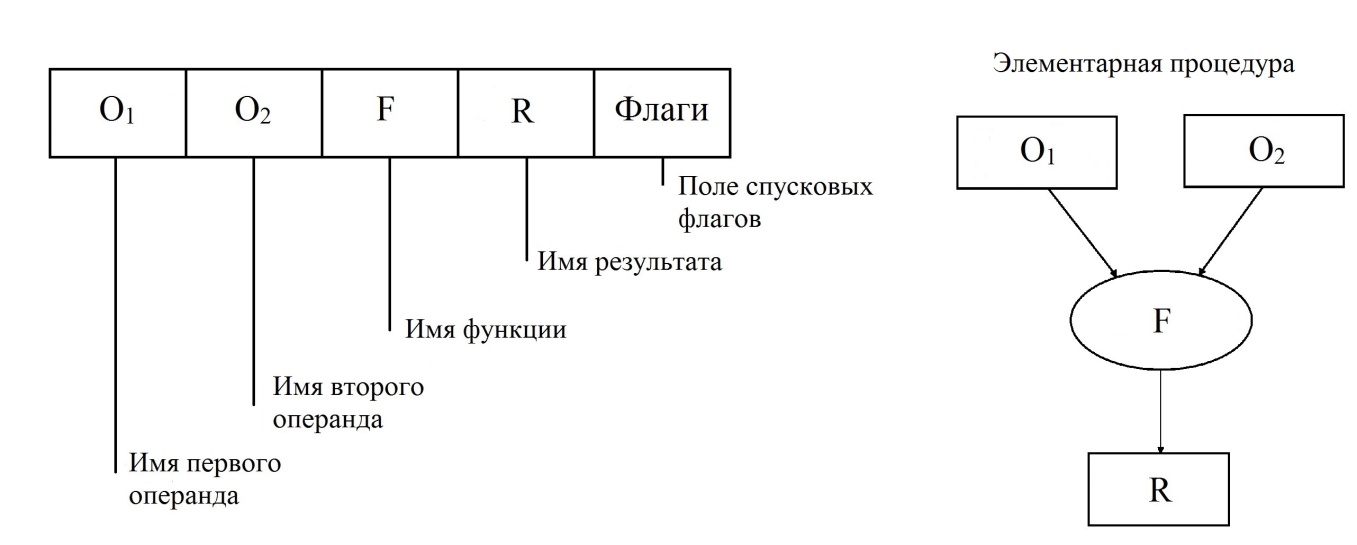
Рис. 22 Структура Data Flow пакета

Data Flow пакет также как и команда описывает элементарную процедуру вычислительного процесса, но в полях пакета записываются имена данных и это делает его языком описания вычислений. Элементарная процедура, описанная пакетом, не фиксирована, как в системе команд классической машины. Принимается гибкая система обозначений, при которой функция пакета может быть машинной командой или программой процедуры. Данные могут быть элементарными операндами или структурами данных. Такая гибкость очень важна при программировании параллелизма. Пакеты размещаются в памяти пакетов в произвольном порядке. В совокупности они образуют запись графа вычислительного процесса. Связность графа поддерживается взаимными ссылками имён аргументов и результатов. Память данных в потоковой машине является многофункциональной. Память данных осуществляет доступ к данным по именам, ведёт учёт их наличия и взаимодействует с памятью пакетов путём посылки фишек с именами поступивших данных. Фишки, принятые в памяти пакетов инициируют операции над спусковыми флагами. В ситуации, когда спусковые флаги пакета сигнализируют о наличии поименованных аргументов, пакет переводится в активное состояние и выставляет маркер готовности. В каждый текущий момент времени в памяти пакетов образуется множество готовых пакетов, которые отправляются на обработку, а в результате их обработки порождаются новые данные, которые спускают на обработку новые порции пакетов. Логика функционирования знаковой системы (языка) машины потока данных не требует специальных мер программирования параллелизма. Знаковая система самостоятельно извлекает динамический параллелизм из текущего состояния данных.

Перечисленные качественные характеристики архитектурной идеи, лежащей в основе проекта Data flow, воспринимаются как более предпочтительные для построения систем с массовым параллелизмом. Однако до настоящего времени неизвестно ни одного варианта их промышленной реализации - проект Data flow не выходит из стадии исследования и разработки. Наш опыт модельных испытаний системы с элементами Data flow, описанный в первой части настоящей статьи даёт тот же результат быстрого прекращения роста производительности на уровне 3-х кратного ускорения при 6 процессорах. Для того, что бы нащупать путь выхода из этого тупика необходимо понять, что объединяет оба проекта, несмотря на обозначенные нами существенные их различия. Общим для классической архитектуры и для проекта Data flow является принцип опережающей разметки трассы процесса. В обоих случаях знаковая система, лежащая в основе архитектуры, является средством создания символьной копии процесса. В классической машине символьная копия процесса существует в виде последовательности команд, а в архитектуре Data flow в виде потокового графа. В классической архитектуре команды считываются синхронно по одной в порядке следования в записи, а в Data flow активируются асинхронно группами в соответствии с логикой спуска по готовности данных. Но и в том и в другом случае активированные команды и пакеты не являются реальными агентами осуществления процессов обработки и вычислений, это только ссылки на данные и на функции. В след за активацией фрагментов трассы процесса разворачиваются потоки обеспечивающих событий, необходимых для поиска, доступа в память, чтения и транспорта данных к местам локализации функций обработки, а за тем по транспорту и размещению в памяти результатов обработки. Основным источником многочисленных накладных потерь являются работы по обслуживанию трассы процесса. Причём, запись трассы в виде потокового графа в Data flow в отличии от линейной последовательности в классической машине, порождает более сложные и объёмные работы по её обслуживанию. Проблема многократного использования стереотипных фрагментов трассы при линейной последовательной записи требует выделения двух точек записи – начала и конца процедуры. Для многократного повторного использования фрагмента потокового графа необходимо обозначить множество входных и выходных полюсов, привязанных к соответствующим вершинам графа. Далее необходимо организовать очереди фишек на входных полюсах, а сами фишки разметить по принадлежности к поколениям данных, возникающим в потоке обработки. Эта проблема получила название задачи раскраски фишек. А затем решать проблему синхронизации потоков фишек на всех входных полюсах процедуры. И всё это ещё не процесс вычислений – это только работы по обслуживанию записи трассы процесса. И это далеко не единственная проблема проекта, но она позволяет понять, почему проект Data flow до сих пор остаётся проектом.

Поищем аналогии в другой области. Похожая ситуация имела место на начальном этапе разработки проекта глобальной сети связи в конце 60-х годов [30]. Географически распределённые сети связи континентального и межконтинентального масштаба управлялись централизованно через центры коммутации. Сети функционировали на базе технологии коммутации цепей. Для осуществления сеанса связи через центры коммутации прокладывался маршрут, который монополизировал дорогостоящие магистральные ресурсы на время сеанса для пары абонентов. Для быстрого обслуживания плотных потоков требований на соединение приходилось наращивать число параллельно работающих каналов. Когда проектировщики задумались о построении глобальной единой автоматизированной системы связи (ЕАСС) и стали подсчитывать необходимые объёмы капитальных вложений оказалось, что проект по стоимости неподъёмный для самых богатых стран и их совместных усилий. Тогда инженеры связисты сделали экспертные оценки эффективности использования магистралей связи. Оказалось, что эффективность их загрузки чудовищно низкая и лежит в пределах нескольких процентов. Существовала проблема выбора - или строить и вводить в эксплуатацию гигантские объёмы новых магистралей или решить системную проблему и поискать более продуктивные технологии связи с лучшими показателями эффективности. Результат нам известен - была создана технология коммутации пакетов, современная глобальная паутина есть ни что иное как сеть пакетной коммутации [31].

В пакетной сети отсутствует централизованное управление и коммутация цепей. Сети равномерно покрывают территории как связные совокупности узлов, где каждый узел связан со смежными узлами, каналами открытого общего доступа. Информация, циркулирующая в каналах, имеет цифровое представление. Сообщения фрагментируются на относительно небольшие порции, которые оформляются в сетевые пакеты. Сетевой пакет это формализованная запись, в которой есть блок фиксации содержательной информации и ряд сопровождающих функциональных полей. Содержательная информация может быть графической, текстовой или звуковой, но сеть к этому безразлична. Интерпретация содержательной информации осуществляется терминальным оборудованием, принадлежащим абонентам. Сеть становится унифицированной. Пакеты порождаются терминальным оборудованием пользователей, большими массами вбрасываются в сеть и начинают самостоятельно продвигаться по сети от узла к узлу. Ресурсы сети никогда не монополизируются отдельными сеансами связи и всегда открыты для доступа. Алгоритмы обработки пакетов в узлах построены таким образом, что пакет может самостоятельно выбирать маршрут и прокладывать свой путь к заданному адресату. Вся необходимая управляющая информация содержится в функциональных полях пакета, сопровождающих поле содержательной информации. В узлах имеются полные каталоги маршрутов и кроме того узлы периодически обмениваются между собой служебными сообщениями, в которых обозначают свою текущую загрузку. Таким образом, пакет на каждом шаге продвижения от узла к узлу уточняет свой маршрут и имеет возможность обхода перегруженных участков сети. В результате сетевая технология пакетной коммутации позволила увеличить продуктивность сетей и эффективность использования магистральных ресурсов на порядки.

Подводя итог обсуждения проблемы эффективности методов организации вычислений можно отметить, что необходимость существенного обновления архитектурной идеи вполне назрела и контуры новой архитектуры определились. Далее мы сформулируем перечень основополагающих принципов новой архитектурной концепции.

Отказ от принципа раздельного существования потоков команд и потоков данных. Должен функционировать один поток - поток данных, сопровождаемых управляющими функциональными полями по аналогии с организацией сетевых пакетов в сетях пакетной коммутации. Основные лексические элементы знаковой системы, организующей вычислительный процесс должны представлять собой самоопределяемые операнды. Самоопределяемый операнд состоит из поля, несущего содержательную информацию, и набора сопровождающих функциональных полей, несущих всю управляющую информацию, детерминирующую поведение и виды активности самоопределяемого операнда.

Отказ от принципа опережающей разметки трассы процесса как следствие отказа от потока команд, которые и были средством формирования символьной копии процесса. По сути это отказ от принципа сосредоточенного управления процессом. Символьная копия процесса отсутствует, а вся управляющая информация распределена по непосредственным участникам процесса – самоопределяемым операндам. Трасса процесса теперь не актуализована в записи программы, а проявляется косвенно в динамике вычислений как результат наблюдения за процессом. Это и есть принцип распределённого управления.

Отказ от технологии коммутации каналов и цепей означает, что обмен данными не должен существовать как отдельная операция, связывающая параллельные фрагменты процесса. При сосредоточенном управлении процессами параллелизм порождает необходимость обмена данными как отдельный компонент процесса, требующий отдельной физической обменной среды. При этом обменные операции, порождают накладные затраты, растущие с ростом параллелизма. В новой архитектуре принимается принцип сетевой организации вычислений, при которой движение данных совмещается с процессом обработки. Практически это означает устранение значительных объёмов паразитных пересылок данных и максимальный параллелизм необходимых обменов данными на низовом уровне, не требующем специальных коммутационных сред.

Перечисленные принципы соответствуют тенденциям, которые фактически сложились в практике построения многопроцессорных систем. Наиболее полное воплощение сетевых принципов организации процессов просматривается в структурах с топологией тора. (См., например, работы [23],[24],[25]). В тороидальных топологиях применяется принцип пакетной маршрутизации данных и главное заключается в том, что в узлах сети размещаются процессорные элементы, а в целом узлы сети совмещают функции обработки и коммутации данных. Осталось сделать лишь завершающее усилие – расширить функции распределённого управления маршрутизацией пакетов до функций управления вычислениями и далее распространить сетевые принципы управления на все уровни организации вычислений.

2.3 Архитектура самоопределяемых данных и принципы распределенного управления

Идея построения архитектуры самоопределяемых данных имеет определённую предысторию, некоторые её фрагменты изложены в ряде публикаций и патентов прошедших лет [17],[32], [33].

Однако в прошлые десятилетия идея не воспринималась как конкурентоспособная. Технология позволяла наращивать производительность вычислительных средств в соответствии с требованиями закона Мура исключительно за счёт роста тактовой частоты и усложнения процессорного элемента. Кроме того смена принципов организации вычислений нарушала требование преемственности и переносимости, наработанных ранее программных продуктов и резкая смена архитектуры была экономически не целесообразна. Но в настоящее время, когда реализация массового динамического параллелизма становится основным направлением развития вычислительных средств, старый проект может стать востребованным и занять определённую нишу в существующем разнообразии областей применения.

Рассмотрим базовые принципы функционирования архитектуры самоопределяемых данных. Основным элементом знаковой системы является самоопределяемый операнд. Это упорядоченная запись, состоящая из содержательного поля, в котором размещается операнд и нескольких сопровождающих функциональных битовых полей. Формат самоопредееляемого операнда приведен на рис. 23

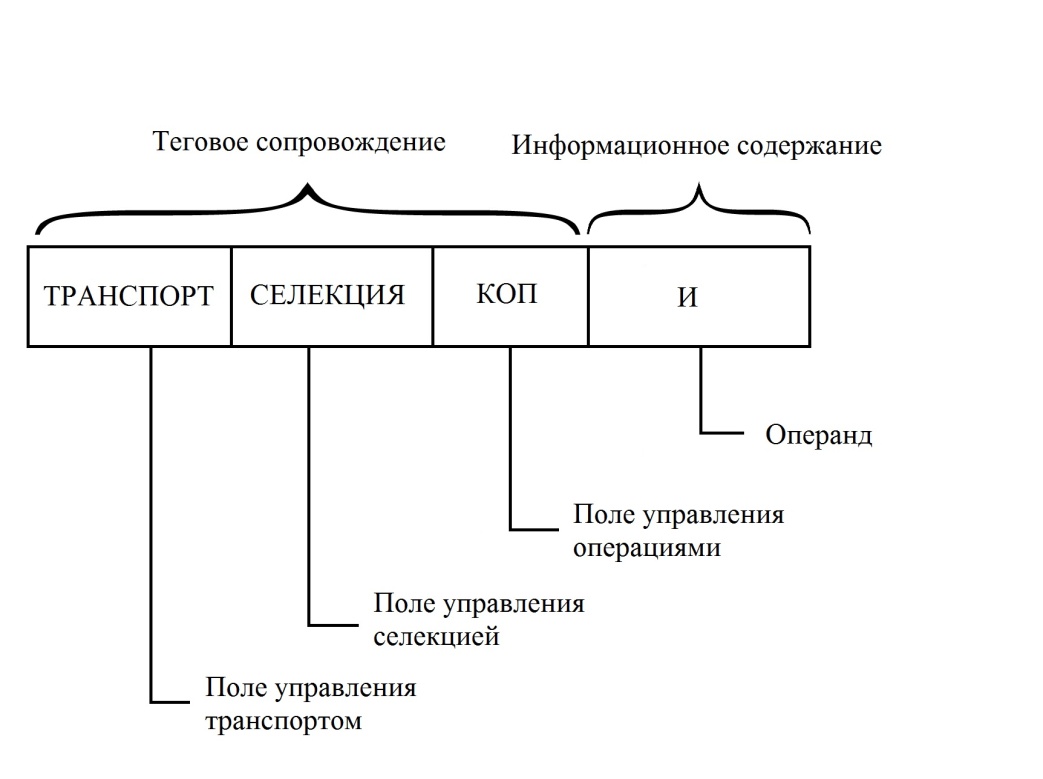
Рис.23 Формат самоопределяемого операнда

Набор функциональных полей называется теговым сопровождением и включает в себя поле управления операциями, поле управления селекцией пар операндов и поле управления транспортом. Кроме перечисленных функциональных полей в теговом сопровождении может быть предусмотрено резервное поле, предназначенное для оперативного расширения управляющих функций в случае необходимости. Это означает, что набор управляющих полей открыт и может корректироваться по текущей обстановке. В приведенном формате рассматривается минимальный набор управляющих полей. Смысл управления состоит в том, что самоопределяемый операнд должен осуществлять селекцию пары для выполнения бинарной операции, определять тип операции обработки и принимать решения о перемещении по транспортным путям вычислительного устройства.

Рассмотрим логику взаимодействия самоопределяемых операндов проиллюстрированную на рис. 24.

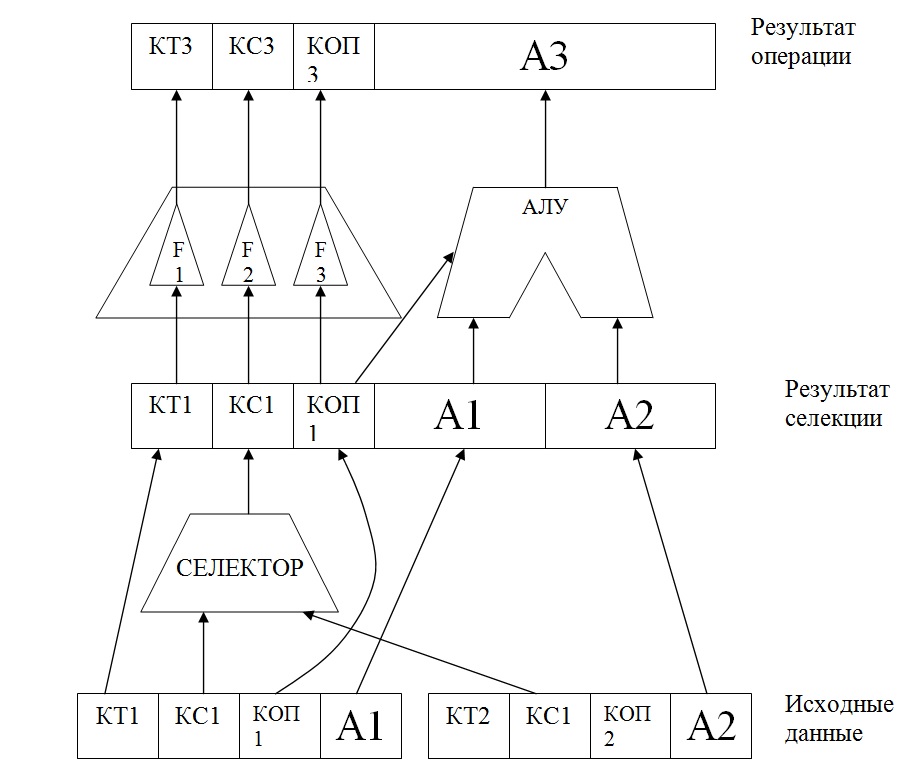
Рис. 24 Схема взаимодействия самоопределяемых операндов

В нижней части схемы изображены два операнда, предназначенные для выполнения заданной бинарной операции. Операция селекции может осуществляться аппаратурой или программно и смысл селекции состоит в том, что селектор отбирает пары операндов по кодовым состояниям полей селекции. На выходе селектора формируется блок, называемый парой. Пара состоит из двух информационных полей A₁ и A₂ , предназначенных для выполнения бинарной операции. К паре пристыковывается теговое сопровождение одного из операндов, второй тег после селекции отбрасывается. Отселектированная пара направляется в канал обработки, который состоит их двух секций – арифметического блока и преобразователя теговых кодов. Арифметический блок это стандартное арифметико-логическое устройство (АЛУ), которое управляется кодом операции из тегового сопровождения пары. Секция преобразования тегов содержит для каждого тегового поля свой унарный функциональный преобразователь. В результате прохождения через канал обработки образуется новый операнд A₃ с новым теговым сопровождением.

Вычислительное устройство состоит из множества каналов обработки и путей перемещения, в которые загружается множество исходных операндов. Поведение исходных операндов определяется кодами их теговых сопровождений. В результате реализации предписанных тегами событий порождается второе поколение операндов с новыми кодами тегов, определяющими следующий шаг обработки.

Для более детального рассмотрения динамики развития процесса обработки введём упрощённый вариант построения самоопроеделяемых операндов. Будем считать, что селекция пар операндов осуществляется по совпадению кодов селекции. Это даёт возможность совместить в одном поле управление селекцией и кодирование операции, поскольку для селекции важен только факт совпадения кодовых значений пары селектируемых операндов. Также с целью упрощения ситуации можно опустить поле управления транспортом. В результате мы станем рассматривать упрощённый самоопределяемый операнд с одним теговым кодом. Схема взаимодействия таких упрощённых операндов изображена на рис. 25.

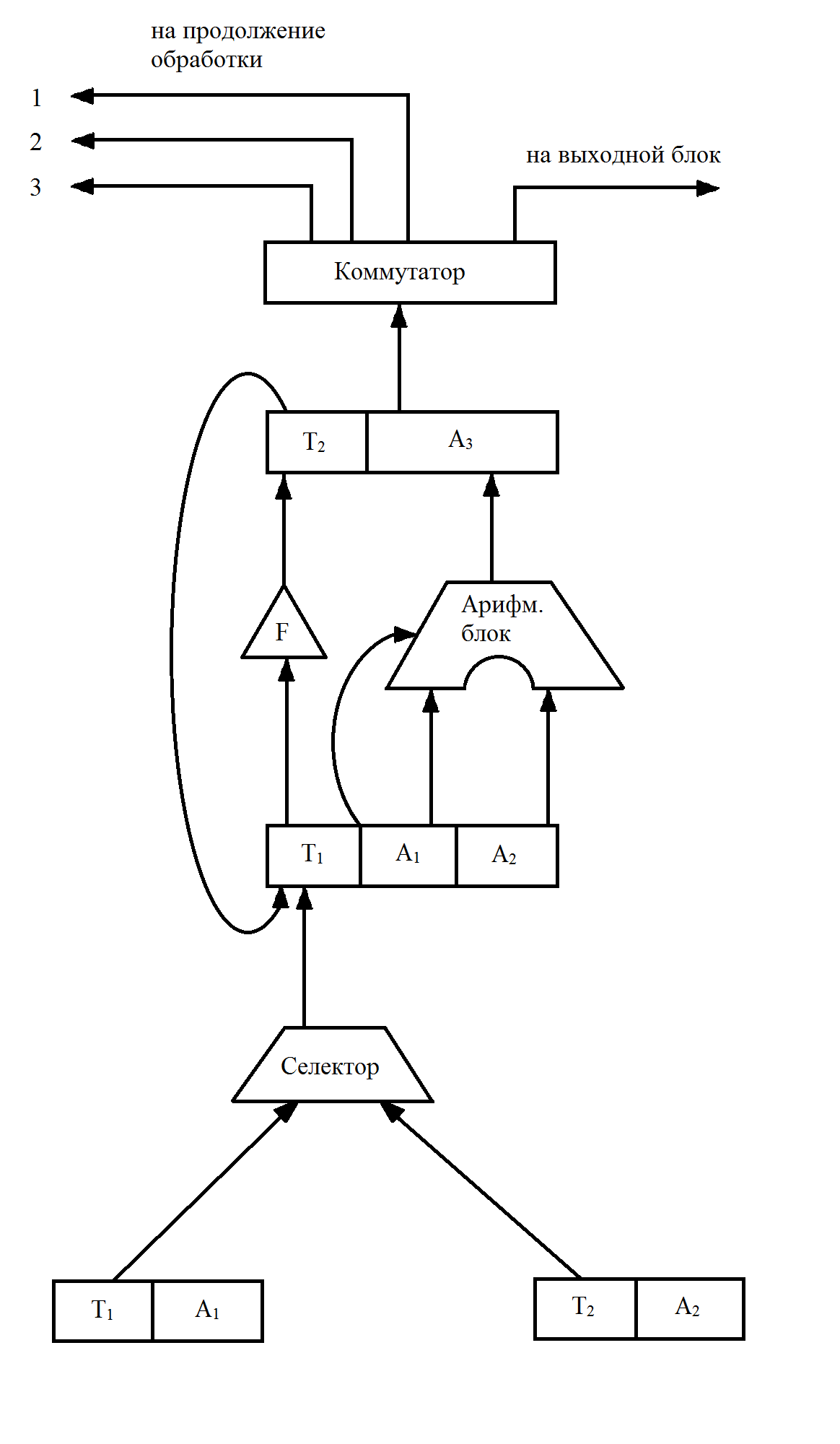
Рис. 25 Схема взаимодействия упрощённых самоопределяемых операндов

Селектор вылавливает в потоке самоопределяемых данных операнды с совпадающими значениями теговых кодов и формирует из них пару. Пара операндов поступает в канал обработки, где над информационными полями выполняются арифметические операции, а теговые коды проходят через дискретный функциональный преобразователь. На выходе канала обработки формируется новый операнд с новым значением тега. На выходе канала обработки изображён коммутатор, в котором определяется выбор направления передачи операнда. Дешифрирующая схема коммутатора анализирует определённые разряды тега и принимает решение о перемещении операнда, либо в выходной блок для формирования выходных данных, либо в одно из трёх направлений продолжения обработки. Таким образом, приведенная схема иллюстрирует, как именно самоопределяемый операнд прокладывает путь своих перемещений в аппаратной среде.

Далее новые поколения операндов вновь вылавливаются селекторами и передаются в каналы обработки, где теговые коды вновь проходят через функциональный преобразователь. Путь превращений теговых кодов выделен на схеме дугообразной стрелкой, замыкающей вход и выход функционального преобразователя. Динамика развития вычислительного процесса осуществляется следующим образом. В секции преобразования теговых кодов всех каналов обработки загружается определённая функция F. В вычислительное устройство вводится набор исходных операндов, с заданными значениями тегов. В силу принятых принципов построения аппаратуры из исходного набора операндов селекторами отбирается множество пар, которые загружаются в каналы обработки для выполнения бинарных арифметических операций. Таким образом осуществляется первый шаг обработки, который полностью определяется состояниями теговых кодов, присвоенных исходному набору операндов. В результате выполнения первого шага на выходе каналов обработки формируется второе поколение операндов с новыми значениями тегов. Далее поведение вновь образованных операндов полностью определяется значениями новых теговых кодов и таким образом осуществляется следующий шаг. Динамическим ядром процесса обработки является рекуррентный генератор кодовых последовательностей, изображённый в правой части Рис. 10. Рекуррентный генератор работает в режиме самообращения и на каждом шаге преобразования передаёт выходной код на входной регистр в качестве нового аргумента.

В классической машине динамика вычислений формируется в результате последовательного считывания программы, которая представляет собой статическую запись опережающей разметки трассы процесса. В самоопределяемых данных процесс разворачивается динамически шаг за шагом и задаётся в аналитической форме в виде функции преобразования теговых кодов F. При этом важно отметить, что в данном случае аналитическое представление динамики процесса не является функцией от времени, а является функцией от предыдущего состояния. В архитектуре самоопределяемых данных роль программы как детерминанта процесса выполняет функция преобразования тегов F и начальные состояния теговых кодов в исходном наборе операндов.

Можно ли в описанной логике взаимодействия самоопределяемых операндов сконструировать осмысленный вычислительный процесс? Рассмотрим конкретный пример на базе введенного ранее упрощённого представления самоопределяемых операндов с одним теговым полем, совмещающим кодирование селекции пар и арифметических операций. Для простоты и наглядности примера будем считать, что тег имеет минимальную разрядность три бита, а функция дискретного кодового преобразователя F есть простая операция сдвига битового набора вправо на один разряд. Трёхразрядный битовый код имеет всего восемь возможных состояний и заданное отображение F можно представить в виде таблицы. Отображение F также можно представить в виде графа, в котором кодовые состояния это вершины графа, а рёбра определяются как пары x; F(x). Назовёт такой граф графом кодовых переходов. Таблица отображения F и граф кодовых переходов приведены на Рис. 11. На графе кодовых переходов для удобства чтения вершины обозначены как целые десятичные числа. Необходимо также назначить кодовым значениям тега арифметические операции и зафиксировать соответствие в виде таблицы, по которой арифметический блок будет интерпретировать теговые коды. Таблица кодирования арифметических операций также приведена на рис. 26. Поскольку кодовых состояний 8, а арифметических операций только 4, целесообразно привязать лишние коды к имеющимся операциям повторно. В данном случае соответствие не должно быть обязательно взаимно однозначным. Код «0» присваивается операции завершения процедуры и интерпретируется аппаратурой как останов.

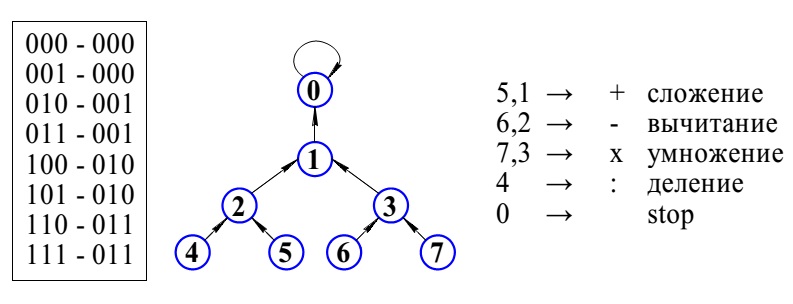
Рис. 26 Таблица отображения F и граф кодовых переходов

Итак, мы сделали все необходимые определения и можем проследить как будет развиваться вычислительный процесс. Графическое изображение процесса в виде графовой диаграммы приведено на рис. 27. Прямоугольниками на диаграмме обозначены операнды, состоящие из двух полей – тега и информационного поля. Пирамидками обозначены процессы, включающие операции селекции пар, арифметические операции и операции преобразования тегов.

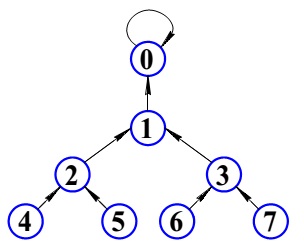
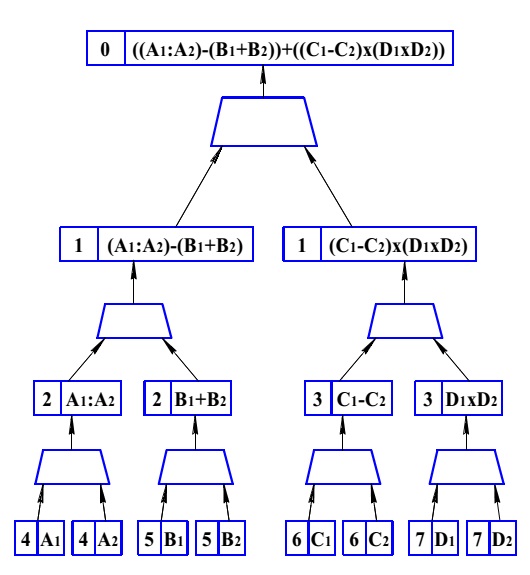
Рис. 27 Диаграмма вычислительного процесса.

Перед началом работы во все каналы обработки вычислительного устройства загружаются преобразователи тегов F и таблицы интерпретации теговых кодов, приведенные на рис. 26. Далее вводится исходный набор операндов. Исходные операнды заполняют нижний слой диаграммы на рис. 27. Теговые коды исходных операндов позволяют отселектирвать пары и направить их в каналы обработки, что отображено во втором слое диаграммы. Третий слой диаграммы заполнен результатами выполнения первого шага обработки, представляющими второе поколение операндов. Формирование содержания полей операндов второго поколения можно проследить по графу кодовых переходов и по таблице интерпретации тегов, которые для наглядности приведены на рис. 27. Преобразования тегов прослеживаются на графе кодовых переходов, а выполняемые арифметические операции определяются таблицей кодирования операций. В информационные поля операндов записывается операция вычисления нового операнда. Во втором поколении операндов в полном соответствии с графом кодовых переходов образуются пары с одинаковыми тегами, которые на следующем шаге обработки вновь отлавливаются селекторами и передаются в каналы обработки. И таким образом события разворачиваются до появления тега со значением «0», что интерпретируется аппаратурой как операция останова и вывода результата в выходной блок.

На данной иллюстрации при изображении операндов следующих поколений, отличных от исходных и порождаемых в процессе обработки, в информационное поле вместо символического обозначения операндов вписаны процедуры их вычисления. Это необходимо для иллюстрации поэтапной сборки заключительного арифметического выражения, описывающего всю наблюдаемую вычислительную процедуру.

Рассмотренный пример показывает, что при заданной логике взаимодействия операндов и некоторых произвольно выбранных начальных условиях в системе развивается детерминированный процесс, соответствующий вычислению определённого арифметического выражения. Параллелизм извлекается аппаратурой из текущего состояния данных и не требует специальных мер синхронизации, привязки данных к каналам обработки и других мер программирования и обслуживания параллелизма. При условии, что во все каналы обработки загружена одна функция преобразования тегов и одна таблица интерпретации тегов, любой операнд может обрабатываться в любом канале. Где операнд оказался в текущий момент, там он и обрабатывается. При этом привязка операнда к определённой позиции на графе процесса обработки содержится в его теговом сопровождении и неотделима от него. Таким образом архитектура самоопределяемых данных ликвидирует накладные потери в виде многочисленных паразитных пересылок данных из мест хранения к местам обработки и обратно.

Для наглядности и простоты примера мы выбрали малое значение разрядности тега, равное трём. Но даже в этом простейшем случае вычисляемое арифметическое выражение оказалось относительно протяжённым и не тривиальным. Достаточно увеличить теговый код на один разряд и число вершин в графе кодовых переходов удвоится, соответственно удвоится и сложность вычислительной процедуры. При 8-разрядном теге граф кодовых переходов с топологией бинарного дерева будет состоять из 256 вершин и 8 этажей, что позволит поддерживать достаточно сложные и многоэлементные вычислительные процедуры. При этом затраты на программирование и поддержку программы (вернее того, что является аналогом программы) останутся незначительными. В классической архитектуре сложность программирования и сложность алгоритма связаны очень просто. Для простой процедуры надо написать десять строк программы, а для сложной тысячу строк. А в самоопределяемых данных для усложнения программируемой процедуры на порядок достаточно только увеличить разрядность тегового кода примерно на три – четыре разряда.

В предыдущем разделе при оценке эффективности разных форм организации вычислений рассматривались механизмы, поддерживающие многократное использование стереотипных фрагментов программы или так называемых стандартных процедур. Было показано, что как в классической архитектуре, так и в архитектуре Data Flow обеспечение перемещаемости процедуры и привязка тела программы процедуры к разным данным является источником огромных издержек и в программном и в аппаратном обеспечении. Посмотрим как эта проблема решается в архитектуре самоопределяемых данных. Рассмотрим тот же пример с обработкой табличных данных, в котором строка таблицы содержит десяток атрибутов, а таблица в целом состоит из нескольких сотен строк. Создаётся процедура обработки строки, для неё формируется функция преобразования тегов F и набор теговых кодов, присваиваемых исходным операндам из строки таблицы. Для тиражирования процедуры и привязки её к разным строкам таблицы достаточно ввести в теговое сопровождение операндов дополнительное поле индексной метки строк таблицы. (В первичных определениях констатировалось, что набор теговых полей открыт для пополнения и введение новых полей не нарушает основы архитектуры и не требует перестраивать конструкцию машины). Тогда все операнды, принадлежащие одной строке таблицы, будут иметь одно значение в индексном поле, а разные строки будут иметь разные индексные метки. Поле индексной метки будет участвовать в операции селекции, но не будет участвовать в преобразовании теговых кодов. Далее можно загружать таблицу в вычислительную среду в произвольном темпе и в произвольном порядке. Операнды, принадлежащие одной строке всегда отселектируются в один процесс обработки строки, а атрибуты разных строк никогда не пересекутся на всех стадиях выполнении процедуры. Любая процедура в архитектуре самоопределяемых данных может быть тиражирована с заданной кратностью путём расширения тегового сопровождения. Дополнительные разряды тега это необходимая плата за обеспечение требуемого свойства. Можно предполагать, что в данном случае издержки окажутся ощутимо меньше чем в классической архитектуре.

В рассмотренном примере реализации процедуры вычисления арифметического выражения функция преобразования тегов, которая является динамическим ядром процесса, порождала граф кодовых переходов с топологией бинарного дерева. Существует целый класс функций, заданных на конечных дискретных наборах и порождающих бинарные деревья разной размерности и с разным распределением кодов по вершинам графа. Понятно, что процесс вычисления арифметического выражения на базе двухместных операций имеет топологию бинарного дерева и может быть размещён на подходящем графе кодовых переходов, порождаемом функцией преобразования тегов. Означает ли это, что в архитектуре самоопределяемых данных можно реализовать только процессы с топологией бинарного дерева?

Рассмотрим возможности расширения разнообразия вычислительных процедур в самоопределяемых данных. Поскольку в машинной обработке приняты двухместные базовые операции, базовые процессы имеют топологию бинарного дерева. Но можно усложнить топологию реального процесса путём склеивания бинарных деревьев в определённых вершинах. Это потребует механизма многократного вхождения некоторых операндов в граф вычислений либо обмена операндами между разными поддеревьями. Создать набор непересекающихся бинарных деревьев можно при условии, что теговый код имеет достаточно большую разрядность и порождает большое дерево. Тогда при одной порождающей функции в графе кодовых переходов можно выделить набор непересекающихся поддеревьев. Локализация поддеревьев определяется выбором листовых кодов. Для привязки групп исходных операндов к своим фрагментам процесса необходимо присвоить им в качестве тегов листовые коды выбранных поддеревьев. Многократное вхождение определённых операндов в граф вычислений можно обеспечить созданием в исходном наборе операндов ряда копий операнда с разными тегами, поскольку именно тег позиционирует место операнда на графе.

Широкие возможности многократного вхождения операндов в граф процесса обеспечивает некоторое усложнение операции селекции путём маскирования части разрядов теговых полей, в частности полей индексных меток. В этом случае возможен множественный отклик при селекции и организация векторной обработки.

Наиболее важным инструментом расширения динамики процессов в системе самоопределяемых данных является механизм операций с шаблонами. Это аналог команд перехода в классической машине. Команда перехода несёт в своём составе адрес новой точки в теле программы и нарушает естественный порядок следования команд путём замены состояния счётчика команд на адрес принудительного перехода. В самоопределяемых данных позиционирование операнда на графе процесса определяется теговым кодом. Смысл операции с шаблоном заключается в том, чтобы принудительно сменить теговый код операнда и перебазировать его в другой фрагмент графа процесса. Шаблон имеет тот же формат, что и самоопределяемый операнд и так же путём селекции находит своего партнёра, но в информационном поле шаблона вместо операнда записан новый тег для партнёра по селекции. При выполнении операции с шаблоном операнд в информационном поле не меняется, а получает новый тег из информационного поля шаблона. Операции с шаблоном позволяют организовать разнообразные условные и безусловные переходы, итеративные циклы и рекурсивные конструкции.

Рассмотренный пример показывает, что организация процессов в архитектуре самооопределяемых данных строится на базе двух компонент – динамического ядра и интерпретатора. Динамическое ядро порождает каркас процесса в виде графа кодовых переходов, а интерпретатор читает порождаемые коды теговых сопровождений операндов и придаёт им содержательное значение, например в виде арифметических операций. Архитектурная идея, не требуя изменений своей сути, допускает разнообразие интерпретаций. Информационные поля операндов могут содержать не только числа, а действия могут выполнять не только арифметические операции. Это могут быть символьные строки и текстовые объекты, это может быть фрагменты графики или структур данных. Рассмотренный нами пример можно воспринимать как вычисление заданного значения, а можно считать его процессом сборки символической записи из базовых лексических единиц. Возможно значительное разнообразие применений архитектурной идеи самоопределяемых данных для построения реальных информационных систем.

Рассмотренный нами пример строился таким образом, чтобы продемонстрировать, что в принятой логике взаимодействия самоопределяемых операндов заданные начальные условия разворачиваются в определённый и осмысленный вычислительный процесс. Но это подтверждает принципиальную состоятельность выдвинутой архитектурной идеи только частично. Необходимо так же показать возможность решения обратной задачи – по заданному процессу построить начальные условия, которые смогут развернуться в этот процесс. Решение этой задачи означает возможность построения технологии программирования процессов в системе самоопределяемых данных. Из рассмотренного примера следует, что технология программирования самоопределяемых данных существенно отличается от привычной технологии программирования классических машин. Суть этого отличия состоит в том, что эвристическое программирование в виде прямой записи символьной копии процесса без привлечения математических инструментов более невозможно. Для построения технологии программирования самоопределяемых данных требуется специальный математический аппарат описания процессов и целый ряд прикладных математических инструментов, разработанных на базе этого аппарата.

2.4 Краткое описание математического аппарата дискретной динамики

Мы будем опираться на ряд фундаментальных работ В.И. Арнольда, которые тематически объединяются одним названием – исследование геометрии функциональных пространств, заданных на конечных множествах. Работы изложены в целом ряде публикаций [34], [35], [36].

Смысл этих работ заключается в том, что исследуется базовое понятие математики – структура, которая задаётся функциональным оператором на конечном множестве элементов. Основная масса исследований структур базируется на аналитической записи оператора и представляется как система манипуляции символическими конструкциями. Арнольд предложил представлять оператор и структуру в целом в виде ориентированного графа. Графовое представление возможно лишь в тех случаях, когда множество, образующее структуру конечно. Граф структуры строится по правилу – элементы структуры являются вершинам графа, а рёбра определяются как пары x; F(x). Возможно только однократное вхождение элемента в граф. Арнольд назвал этот граф монадой. Этим архаичным названием подчёркивалось фундаментальное значение введенного понятия как древнего первоосновного. Традиция исследования монад восходит к Ньютону, Лейбницу и возможно имеет и более ранних предшественников. Арнольд отмечает, что первоначально построение монад носило эмпирический характер и оказалось интригующим и увлекательным занятием. В последствии ученики и аспиранты применили компьютеры для построения монад и дело двинулось более высокими темпами.

Основные свойства монад достаточно очевидны и следуют из первичных определений. В монаде всегда есть хотя бы один цикл, это следует из конечности исходного множества. Поскольку оператор образующий структуру всюду определён, в некоторый момент для результата применения оператора не хватит элементов и результат замкнётся на ранее использованных. Если граф монады содержит несколько циклов, множество распадается на непересекающиеся классы элементов, тяготеющих к своему циклу. Это происходит потому, что между циклами рёбер не может быть, в противном случае нарушается функциональность отображения F. На рис. 28 приводится перечень возможных структур графов монад.

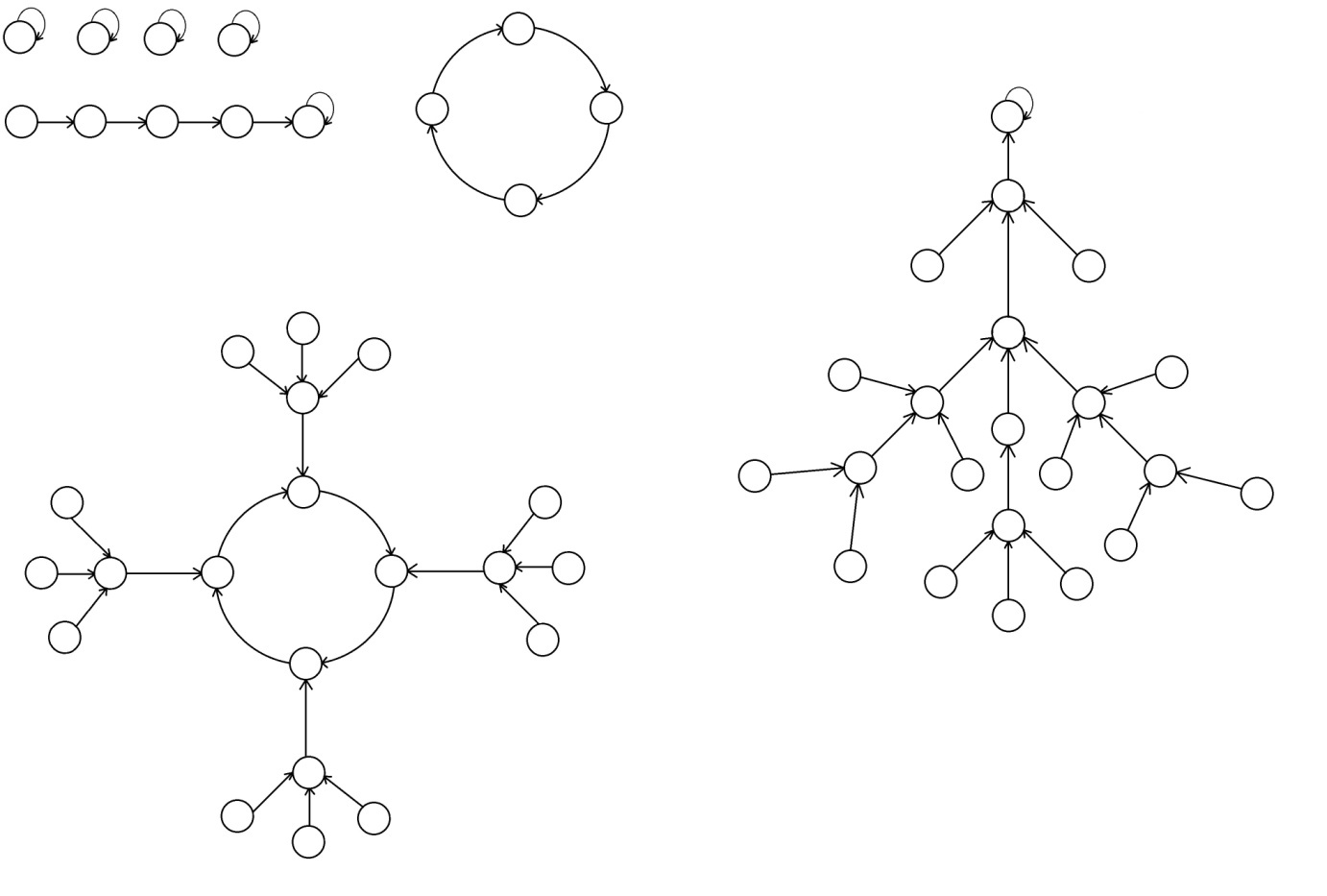
Рис. 28 Примеры графов монад

Множество элементов, тяготеющих к своему циклу Арнольд назвал аттрактором. Исследования конечных структур, представленных монадами использовались Арнольдом для построения шкалы оценки сложности математических объектов, для исследований в теории чисел и ряде других направлений.

Представление структуры в виде монады позволяет увидеть тонкие закономерности и свойства, которые ускользают или маскируются при аналитической записи. Так, например, рассмотрим структуру, образованную дискретным функциональным преобразователем, заданным на множестве состояний компьютерного регистра. Оператор, может представлять собой арифметическое соотношение или булеву функцию, составленную из набора побитовых булевых операций. Построение монад для данной структуры обнаруживает неожиданный факт - структура графа монады зависит от числа элементов образующего множества. При изменении разрядности регистров и неизменном функциональном операторе структура графа претерпевает значительные изменения. Пример иллюстрируется на рис. 29. Оператор F представляет собой следующую последовательность элементарных операций: над исходным операндом выполняется операция циклического сдвига на один разряд, далее полученный результат складывается с исходным операндом по модулю 2. На рис. 29 Приводятся графики заданного отображения F при разных значениях разрядности регистров и соответствующие им графы монады.

Разрядность 3.

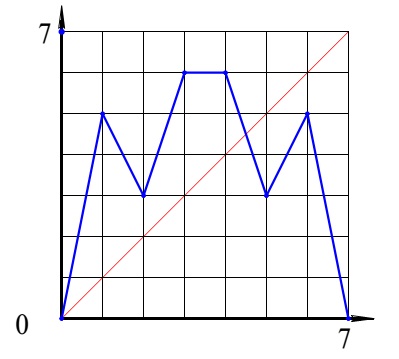
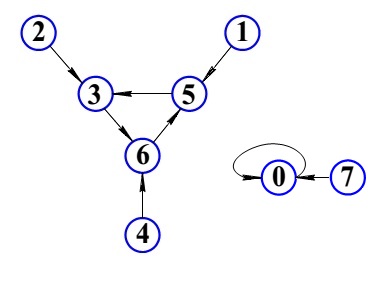
Разрядность 4.

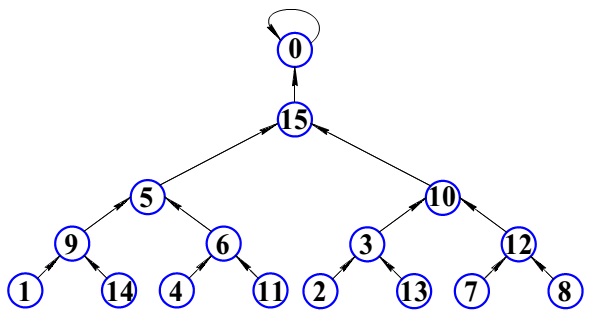
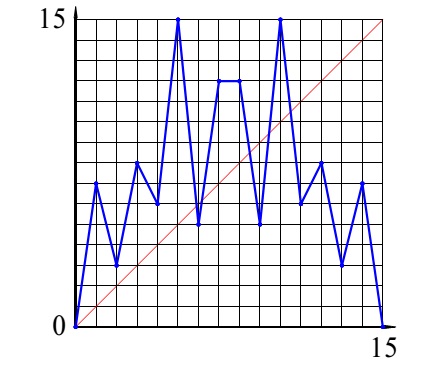
Разрядность 5.

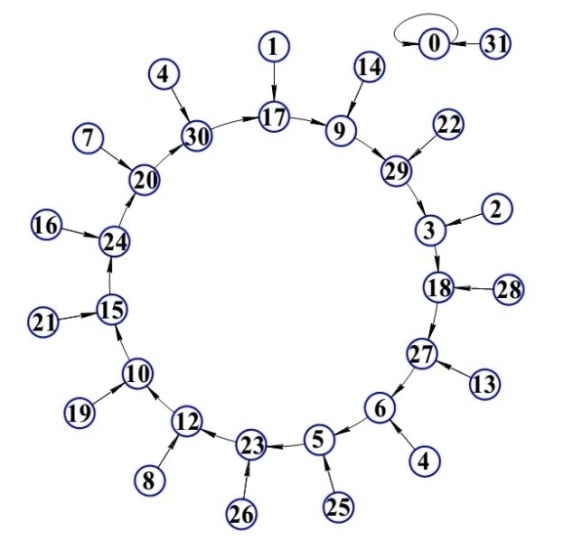
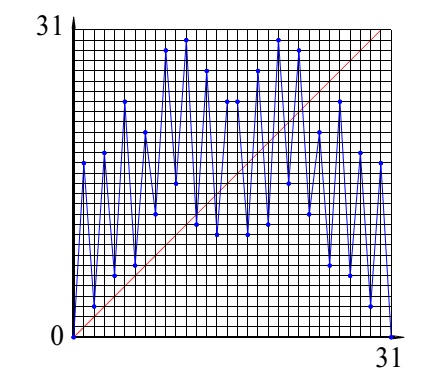
Рис. 29 Зависимость структуры графа монады от числа элементов образующего множества

Данные получены эмпирически и демонстрируют целый ряд нетривиальных закономерностей. Интересующее нас односвязный граф с топологией бинарного дерева проявляется при разрядности 4, затем наблюдается при разрядности 8 и далее повторяется с определённой периодичностью. На приведенных иллюстрациях мы вынуждены ограничиться простейшими картинками при малой разрядности регистров, но этого достаточно для понимания существенных изменений топологии графа монады при изменении числа исходных элементов. Этот эффект проявляется не для всех функций, образующих структуру. Отразить эти факты в аналитической записи структуры либо невозможно, либо очень не просто.

Мы примем за основу метод графового представления структур на конечных множествах с целью разработки дискретной динамики, как инструмента описания процессов в среде самоопределяемых данных.

Мы не будем рассматривать абстрактные множества, а ограничимся изучением вполне конкретных ситуаций во внутренней среде компьютера. Исходными множествами в нашем случае будут конечные наборы регистровых состояний, которые можно представлять как битовые векторы определённой разрядности, либо записывать их как целые положительные натуральные числа. Операторы, образующие структуры на множествах регистровых состояний представляют собой дискретные преобразователи, которые можно реализовать аппаратно как логические схемы либо программно как наборы компьютерных команд. Оператор задаётся как функция и реализует функциональное отображение. Метод исследования структуры основан на представлении целочисленной функции в виде графа. Здесь требуется разъяснение – какая связь существует между функцией и графом.

Рассмотрим график целочисленной функции, заданной на конечном отрезке. Это будет совокупность точек на целочисленной решётке. Линия, соединяющая точки носит условный характер и может быть опущена. Совокупность точек на квадратной целочисленной решётке можно рассматривать как матрицу смежности, задающую ориентированный граф, рёбра которого есть совокупность пар вида x; F(x). Так, что представление функции в виде ориентированного графа в данной ситуации совершенно естественно, хотя и непривычно. Поскольку функция определена на регистровых состояниях, станем называть этот граф графом кодовых переходов и обозначать G_F , граф, порождаемый функцией F.

Каждая точка графика целочисленной функции имеет две проекции - на ось x и на ось y. Если график функциональный, то на все точки оси x всегда имеется одна и только одна проекция графика. На точки оси y может проецироваться любое число точек графика, в том числе и ни одной. Из этого следует, что на графе кодовых переходов каждая вершина всегда имеет одно и только одно исходящее ребро. Входных рёбер может быть сколько угодно от 0 до N, где N число состояний регистра. Следовательно, все возможные графы кодовых переходов образуют специфический класс графов, ограниченный определёнными правилами структурообразования.

На рис. 30 можно проследить как свойства графика функции F проецируются на свойства графа кодовых переходов.

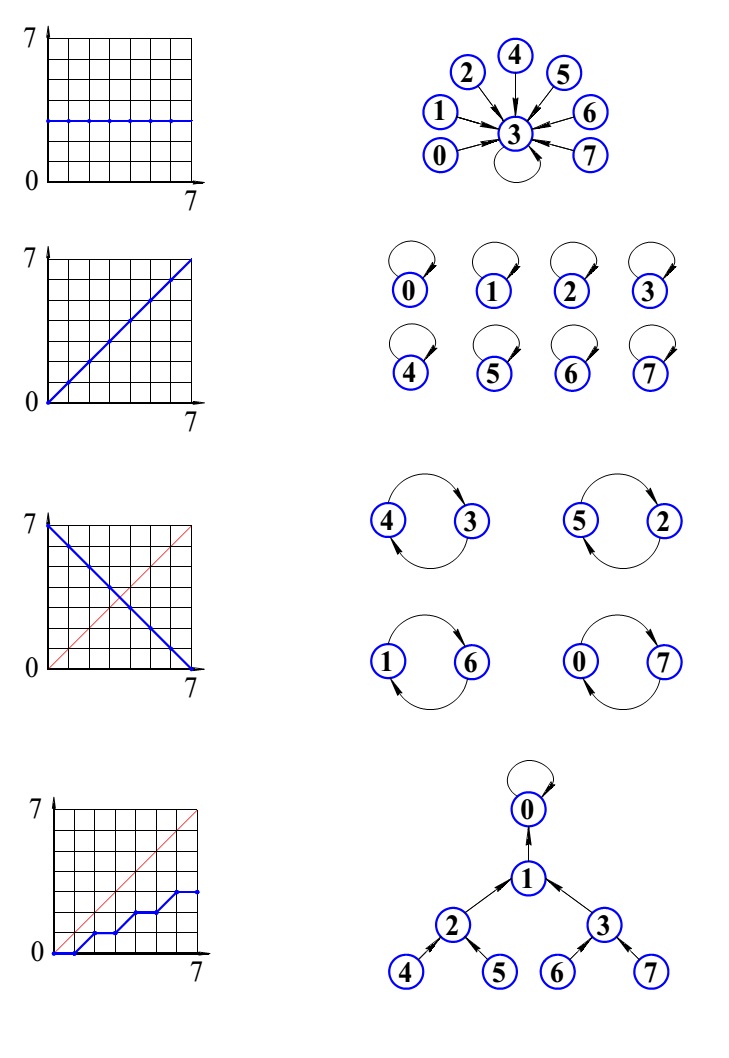
Рис. 30 Взаимосвязи графика функции и порождаемого графа G_F

Определённая таким образом структура может рассматриваться как математическая модель среды, в которой функционируют самоопределяемые данные. Здесь могут быть представлены кодовые состояния тегов и функции преобразования тегов. Ранее было показано, что динамика поведения самоопределяемых данных порождается процессом смены значений теговых кодов, которые на каждом шаге обработки проходят через функциональный преобразователь. Когда значения функции используются в качестве аргументов, выполняется операция суперпозиции и она применяется многократно, что изображено на рис. 31а. А поскольку в этой длинной цепи на всех шагах преобразований функции F одна и та же, мы имеем операцию автосуперпозиции. Сокращенно операцию автосуперпозиции можно изобразить в виде замкнутой схемы, приведенной на рис. 31б.

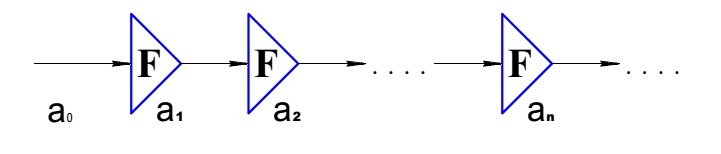
Рис. 31а Суперпозиция

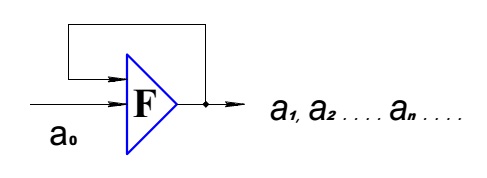
Рис. 31б Автосуперпозиция

По сути это рекуррентный генератор, порождающий кодовые последовательности. Если мы хотим понять динамику развития кодовых последовательностей, порождаемых рекуррентным генератором мы должны обратиться к графу кодовых переходов. Порождаемые рекуррентным генератором кодовые последовательности есть маршруты на графе кодовых переходов и их динамика определяется структурой графа.

А теперь можно сделать определения основных понятий дискретной динамики:

дискретный аттрактор это динамическая система, имеющая в своём составе множество регистровых состояний R, функциональный оператор F, отображающий R в R и оператор автосуперпозиции F.

Фазовый портрет дискретного аттрактора это граф кодовых переходов G_F порождаемый функцией F.

Состояние совокупности самоопределяемых операндов в текущий момент фиксируется состояниями их теговых кодов. Теговые коды размещаются на вершинах графа кодовых переходов, т. е. на фазовом портрете дискретного аттрактора. Смена теговых кодов может осуществляться только переходом в смежные вершины на фазовом портрете.

Дискретный аттрактор задаёт функциональное пространство, в котором существуют самоопределяемые данные. Граф кодовых переходов формирует геометрию этого пространства как совокупность путей преобразования теговых кодов и именно таким образом выполняет роль фазового портрета аттрактора.

Силовой агрегат или движок, который осуществляет перемещения на фазовом портрете это процедура автосуперпозиции, реализованная как рекуррентный генератор. Рекуррентный генератор это процедура самообращения, подающая выходной результат вновь на вход преобразователя. Именно самообращающаяся процедура выполняет роль динамического ядра процесса.

Фазовый портрет это математическая абстракция, Граф кодовых переходов не реализуется физически, например аппаратно как схемный лабиринт, по которому перемещаются самоопределяемые операнды или программно как сетевая структура данных. Фазовый портрет задаётся косвенным образом как результат взаимосвязанных трансформаций теговых кодов. Обширные фазовые портреты могут поддерживаться очень скромными аппаратными затратами. Если теговый код содержит 16 двоичных разрядов, а программа реализации оператора F состоит из менее чем десяти машинных команд, аттрактор поддерживает фазовый портрет в виде графа кодовых переходов, состоящего из сотен тысяч вершин. Уровень компрессии средств фиксации аттрактора в данном случае может составлять примерно 4 - 5 порядков. По этой причине появляется возможность не хранить детерминанты процесса в одном устройстве, осуществляющем сосредоточенное управление вычислениями, а разместить средства фиксации дискретного аттрактора непосредственно в каждом операнде и осуществить принцип распределённого управления.

Если все теговые сопровождения операндов обрабатываются одним преобразователем F, все они принадлежат одному фазовому портрету, а их теговые коды позиционируют всех и каждого на определённых вершинах графа кодовых переходов. В результате множество никак не связанных единым управлением операндов функционирует как строго согласованный ансамбль, двигающийся по заданным траекториям и реализующий заданный процесс. Уместно назвать этот эффект функциональной когерентностью.

Функциональная когерентность обеспечивается высокой степенью компрессии средств фиксации дискретного аттрактора. А компрессия возможна вследствие глубокого вырождения комбинаторики структурообразующих факторов, что означает потерю возможности задавать любые мыслимые и не мыслимые структуры фазовых портретов. В условиях компрессивного представления средств фиксации аттракторов возможные фазовые портреты образуют узкий класс структур, подчиняющихся жёстким ограничениям. Означает ли это потерю универсальности программирования любых приложений – вопрос дискуссионный. Во всяком случае следует учитывать, что не любая последовательность команд классической машины может быть осмысленной программой.

Все кодовые траектории в дискретном аттракторе сходящиеся и завершаются попаданием в цикл на графе G_F. Если цикл состоит из одной вершины, процесс останавливается. Это точка покоя дискретного аттрактора. Если цикл содержит множество вершин, аттрактор бесконечно повторяет заданную последовательность, что можно интерпретировать как постоянное циклическое выполнение определённого действия, например сканирования и контроля текущих параметров системы управления. Дискретный аттрактор обладает свойством устойчивости. Если внешнее воздействие или повреждение выбросит его из точки покоя, аттрактор сам, в соответствии с его устройством начнёт двигаться, а любые траектории движения аттрактора есть маршруты на фазовом портрете, которые всегда сходятся к точке покоя. В точке покоя механика аттрактора не выключается. Рекуррентный генератор кодовых последовательностей устроен таким образом, что в результате автосуперпозиции на выходе бесконечно порождается один и тот же код. Для внешнего наблюдателя это выглядит как останов. На самом деле дискретный аттрактор никогда не останавливается. Останов дискретного аттрактора носит условный характер, это стабильное состояние динамического равновесия, которое можно интерпретировать как непрерывный контроль равновесного состояния.

Дискретный аттрактор как динамическая система обладает определённой спецификой, которая в первую очередь заключается в том, что при формировании динамики не используется категория времени. Динамика дискретного аттрактора основана на отношениях предшествования и каждое следующее состояние порождается как функция от предыдущего. В простейшем случае, когда параллельный процесс развивается в рамках одного аттрактора по единому фазовому портрету, все события увязаны отношениями предшествования, определяемыми графом кодовых переходов. Но при усложнении ситуации, предполагающей взаимодействие процессов, размещённых на разных аттракторах, придётся решать проблему определения одновременности событий в функциональных пространствах, в которых размещены и двигаются самоопреоедяляемые данные. С этой целью придётся вводить понятия меры и измерения расстояния на фазовых портретах. При этом понадобится осуществлять переход от представления процесса как функции от предыдущего состояния к его представлению как функции от номера шага или длинны расстояния на фазовом портрете. Это одна из важнейших задач развития дискретной динамики.

Актуальной задачей дискретной динамики является конструирование фазовых портретов с заданными свойствами или, что то же, построение графов кодовых переходов с заданной топологией. Первые шаги становления дискретной динамики сделаны чисто эмпирически. С помощью простой инструментальной программы задавались рекуррентные генераторы с определённой разрядностью регистров и определённой функцией преобразования кодов и для каждого генератора строился граф кодовых переходов G_F.

Таким образом была сформирован базовая библиотека рекуррентных генераторов, представляющая базовые конструкции. Базовые конструкции известны и изображены на рис. 28. В вольной терминологии мы можем их перечислить. Это наборы самовозвратных полюсов, цепи, деревья, кольца, и розетки, представляющие собой деревья и цепи, пристыкованные к вершинам кольца. Самоовозвратными полюсами мы называем петли или минимальные циклы, состоящие из одной вершины. При этом граф может быть связен или иметь несколько компонент связности со своими циклами.

Для создания инструментальных средств дискретной динамики необходимо найти процедуру, позволяющую строить сложные конструкции фазовых портретов из простых базовых. Такая процедура существует и называется конкатенация. В наших условиях конкатенация означает совмещение двух и более регистровых секций в определённом порядке. В результате конкатенации образуется новый регистр, в котором правая секция выполняет роль младших разрядов, а левая секция роль старших разрядов объединённого регистра. Если регистры входят в состав рекуррентных генераторов и над ними построены функциональные преобразователи, в результате конкатенации образуется новый рекуррентный генератор, в котором и регистры и преобразователи образуются путём совмещения участников операции конкатенации. Иллюстрация операции конкатенации приведена на рис. 32.

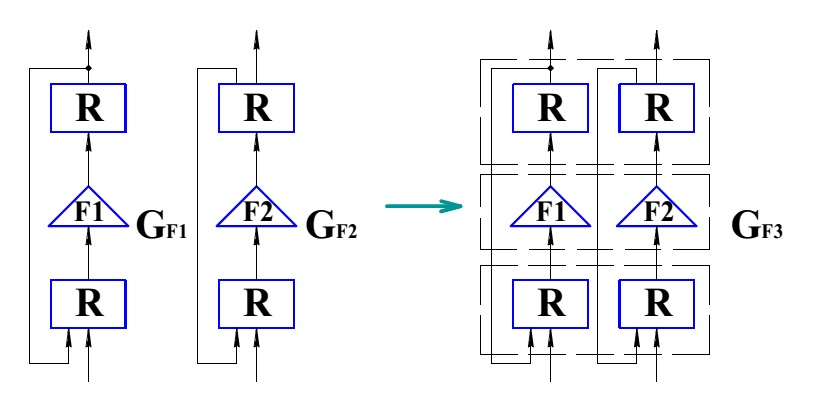
Рис. 32 Конкатенация рекуррентных генераторов

Операция конкатенации объединяет два рекуррентных генератора, заданных функциями F1 и F2. Каждый из участников операции порождает свой граф кодовых переходов G_F1 и G_F2. В результате конкатенации и совмещения двух исходных рекуррентных генераторов образуется новый результирующий, который порождает новый граф кодовых переходов G_F3. Структура нового графа может существенным образом отличаться от структур участников конкатенации, а примитивная инженерная операция совмещения регистровых секций с математической точки зрения реализует нетривиальную операцию над графами. Далее приведены некоторые примеры операций над графами, возникающими при конкатенации рекуррентных генераторов.

Так, например, при конкатенации двух бинарных деревьев получается тернарное дерево. При этом глубина дерева сохраняется, а кратность ветвления умножается, рис. 33.

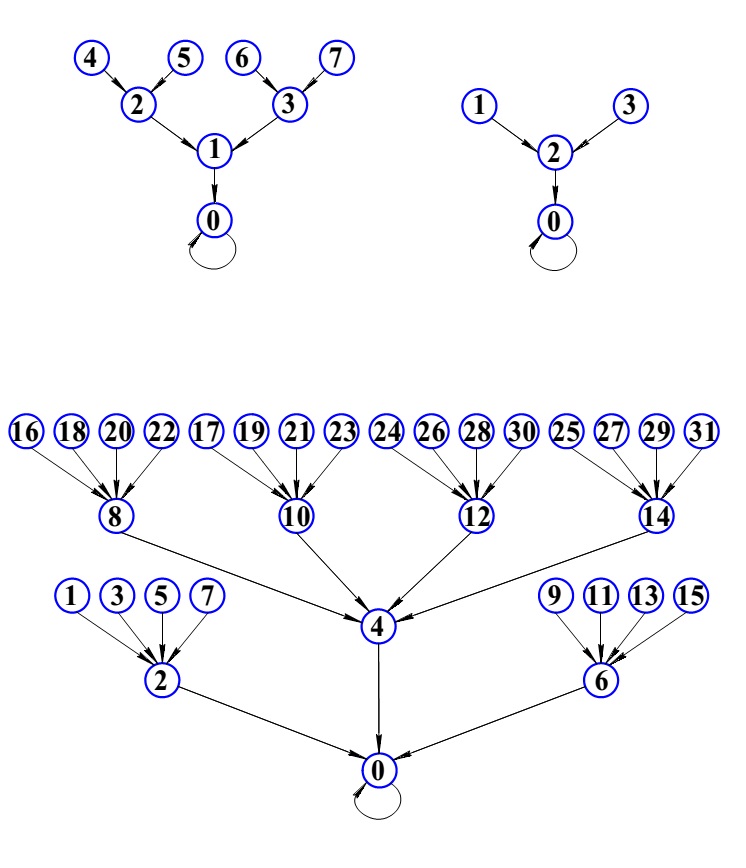
Рис. 33 Конкатенация двух бинарных деревьев

При конкатенации дерева и набора полюсов получается набор деревьев, т.е. связный граф превращается в многосвязный и число компонент связности равно числу полюсов в одном из участников конкатенации, рис. 34.

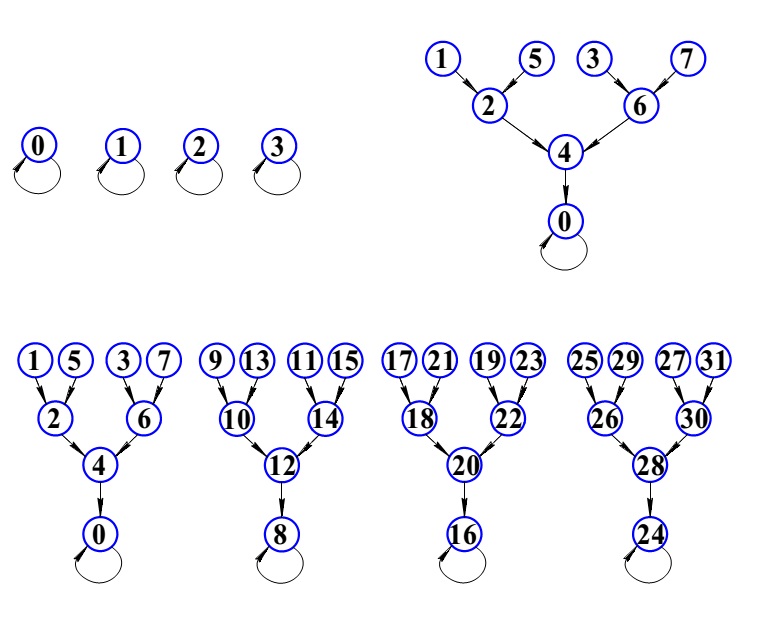
Рис. 34 Конкатенация дерева и набора полюсов

При конкатенации кольца и дерева, происходит образование розетки, представляющей собой набор деревьев пристыкованных к вершинам кольца, рис. 35.

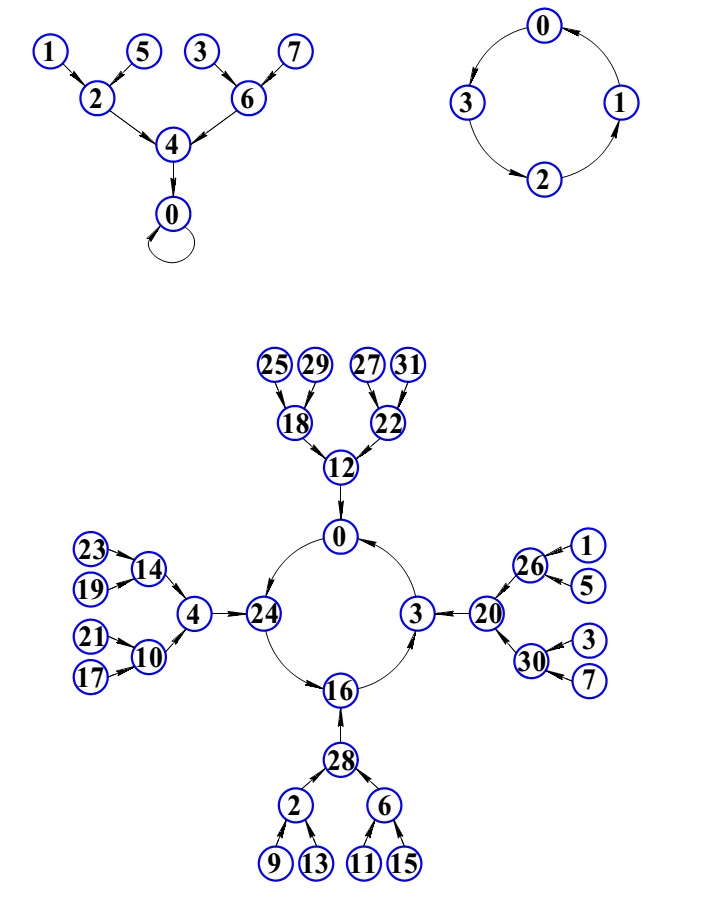
Рис. 35 Конкатенация кольца и дерева

Эмпирически удалось сформировать базу данных по конкатенации разных вариантов графов кодовых переходов и выделить набор практических приёмов конструирования структур, необходимых для решения ряда практических задач. Дальнейшая разработка этого направления должна привести к обоснованию свойств операций конкатенации и построению алгебры операций над графами кодовых переходов.

До сих пор мы рассматривали варианты использования графа кодовых переходов как динамического ядра дискретного аттрактора, в котором продвижение по фазовому портрету происходит в направлении от листьев к корню дерева и циклу, которым завершается компонента связности. Для практических приложений дискретной динамики важно также обеспечить возможность продвижения по фазовому портрету в обратном направлении – от корня дерева к листьям. Эта задача не может решаться средствами функционального оператора, поскольку обратное отображение является многозначным и должно поддерживать ветвящийся процесс. Для поддержки ветвящегося процесса можно использовать гирлянду функциональных преобразователей. Гирлянда изображена на рис. 36

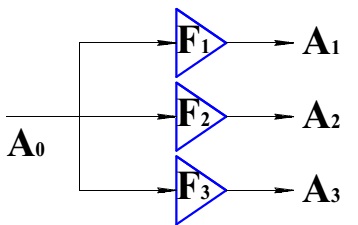
Рис. 36 Гирлянда функциональных преобразователей

Для примера выбрана гирлянда из трёх функциональных преобразователей, их число может меняться. Принцип действия гирлянды следует из её схемного изображения. При подаче на вход некоторого начального значения кода A₀ гирлянда откликается тремя выходными значениями А₁ , А₂ , А₃ . Далее каждое из них может подаваться на вход гирлянды и порождать на выходах следующие три значения. В данном случае рекуррентный генератор, построенный на базе гирлянды, порождает ветвящийся процесс, который носит расходящийся характер. Таким образом вводится новый базовый элемент дискретной динамики - дискретный репеллер. Дискретный репеллер это расходящийся процесс, порождаемый гирляндой функциональных преобразователей и операцией автосуперпозиции гирлянды. Фазовый портрет репеллера это расходящийся граф кодовых переходов гирлянды. Репеллер по определению не имеет остановки и порождает бесконечный расходящийся процесс. Вследствие конечности набора кодов, на котором определены функциональные преобразователи гирлянды рано или поздно запас кодов исчерпывается и на выходе гирлянды появляется код, который ранее уже имел вхождение в вершины графа кодовых переходов. Это означает, что фрагмент дерева, начинающийся с данной вершины будет воспроизведен репеллером вновь. В целом фазовый портрет репеллера будет состоять из бесконечного повторения конечного набора фрагментов, графа кодовых переходов, заданного гирляндой. Исследование динамики развития процессов в репеллерах это следующий и очень содержательный раздел дискретной динамики.

Опираясь на понятия дискретный аттрактор и дискретный репеллер можно сформулировать важное для приложений дискретной динамики понятие реверсивный аттрактор. Допустим, что задан дискретный аттрактор с определенным фазовым портретом. Для построения реверсивного аттрактора необходимо синтезировать репеллер, фазовый портрет которого совпадает с фазовым портретом аттрактора с точностью до инверсии направления рёбер графа кодовых переходов. Реверсивный аттрактор это сопряжённая пара аттрактора и репеллера, обеспечивающая продвижение процесса по заданному фазовому портрету в прямом и обратном направлениях. Задача эта решается следующим образом. Исходный аттрактор задаётся рекуррентным генератором на базе определённой целочисленной функции. График функции представляется как совокупность точек на целочисленной квадратной решётке. График изображён на рис. 37а.

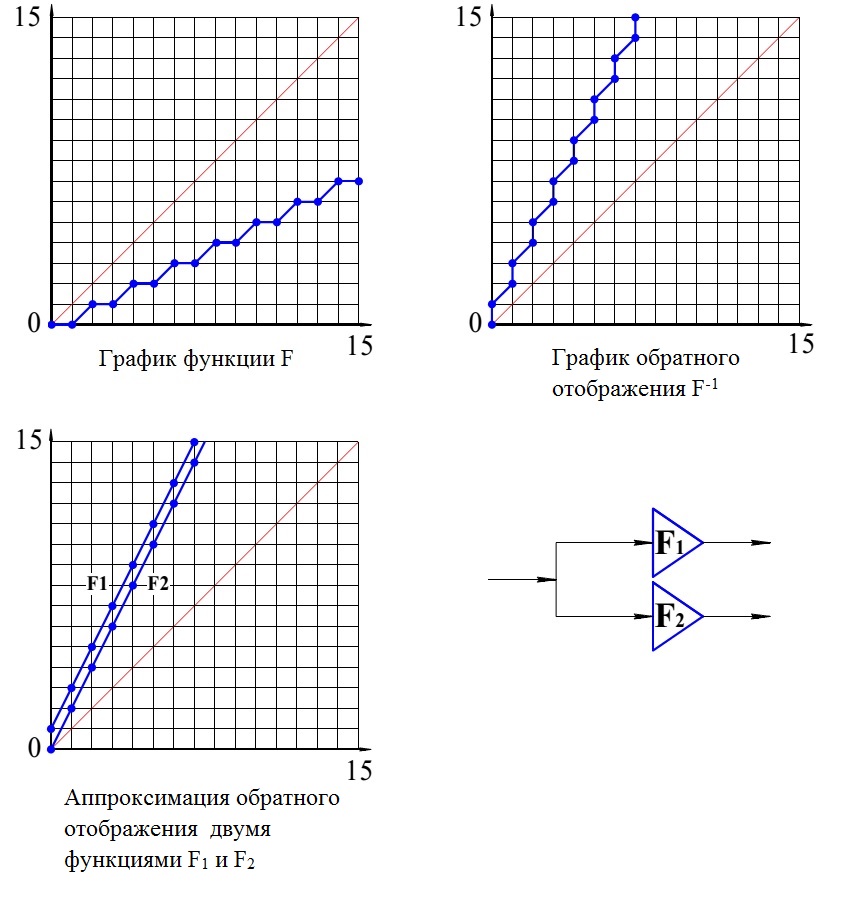
Рис. 37 Процедура построения реверсивного аттрактора

По данному графику необходимо построить обратное отображение. Для этого надо выполнить операцию замены координат, что достигается поворотом исходного графика вокруг главной диагонали. График обратного отображения изображён на рис. 37б. Обратное отображение не является функциональным и далее надо решить задачу синтеза набора сопряжённых функций, покрывающих, полученный график обратного отображения. Перечисленные действия изображены на рис. 37

Эта задача не имеет общего решения. В каждом конкретном случае путём подбора можно найти множество вариантов покрытия графика обратного отображения функциональными графиками и искать среди них приемлемые по критерию удобства реализации сопряжённых функций. Из полученного таким образом набора сопряжённых функций составляется гирлянда для реализации репеллера, дополнительного к заданному аттрактору.

Рассмотренные до сих пор средства формирования графов кодовых переходов предполагают, что каждое регистровое состояние из множества, образующего структуру имеет однократное вхождение в граф кодовых переходов. В практике применения дискретных аттракторов для формирования вычислительных работ необходимо обеспечить многократную повторяемость кодов операций на графе вычислительного процесса. Это достигается путём наложения маски на образующие регистры и чтения из под маски только части разрядов, необходимых для кодирования операций. Рассмотрим конкретный пример. Необходимо построить граф кодовых переходов со структурой сильно ветвящегося дерева с кратностью ветвления равной 8 и заданной глубиной 4 уровня. При этом ставится задача обеспечить возможность полной нумерации предшественников каждой вершины. Выберем определённую вершину и рассмотрим набор из восьми вершин, являющихся предшественниками данной. Коды вершин предшественников должны быть устроены таким образом, чтобы при наложении на них определённой маски можно было извлечь три разряда, задающих полную нумерацию предшественников от 0 до 7, или в двоичном выражении от комбинации 000 до 111. По принятому условию это свойство должно выполняться для всех вершин кроме листовых, которые не имеют предшественников.

Искомый рекуррентный генератор, поддерживающий заданное сильно ветвящееся дерево будет сформирован в результате конкатенации трёх генераторов, поддерживающих четырёхэтажные бинарные деревья и построенные на базе уже известной нам функции сдвига вправо на один разряд. По известным нам свойствам операции конкатенации бинарных деревьев глубина сохраняется равной 4, а кратности ветвления перемножаются и дают требуемое значение 8. В итоге получается полное четырёхэтажное дерево с кратностью ветвления равной 8. А теперь наложим на образующие регистры маску, которая позволяет извлечь из каждой секции участвующей в конкатенации один младший крайний правый разряд. Трехразрядный код, извлечённый в результате маскирования, содержит полную нумерацию вершин предшественников. Остальные разряды полного кода позиционируют вершины на дереве в целом. На рис. 38 приведен фрагмент сильно ветвящегося дерева с реальными значениями кодов вершин и показано извлечение полной нумерации вершин предшественников.

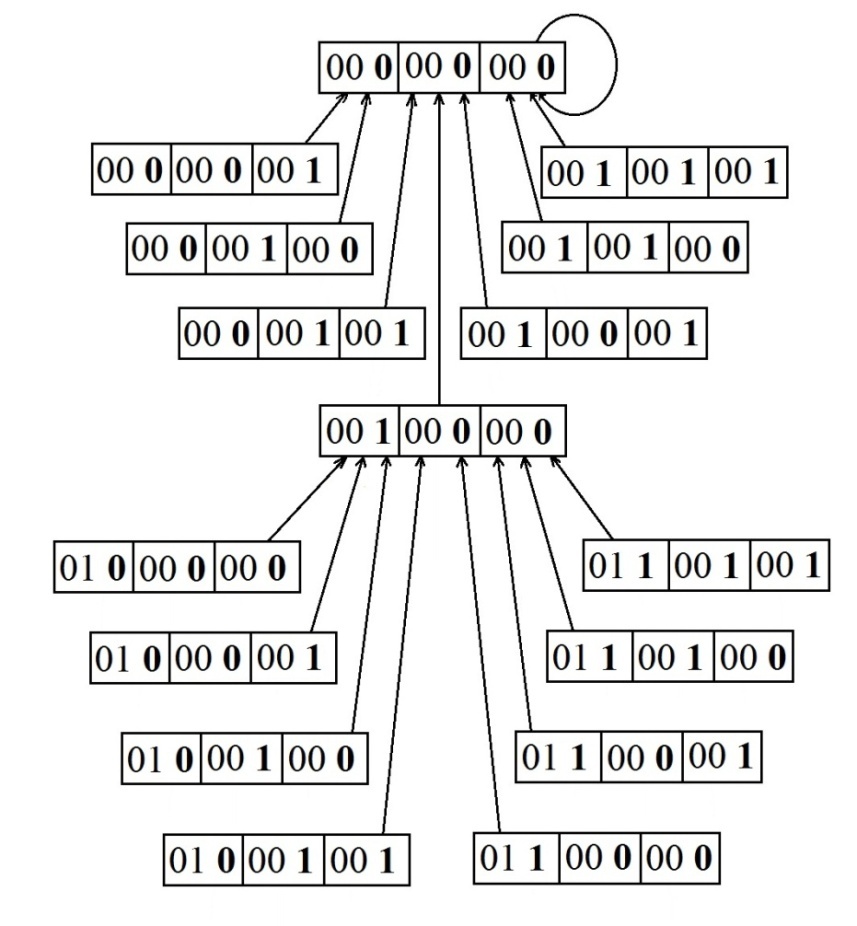
Рис. 38 Извлечение из-под маски полной нумерации вершин предшественников

Разряды кодов, извлекаемые маской обозначены жирным шрифтом и отделены пробелом.

Весь объём изложенных выше понятий и механизмов дискретной динамики необходим для обсуждения возможной технологии программирования вычислений в архитектуре самоопределяемых данных. Задача ставится следующим образом: задано арифметическое выражение, по которому строится граф вычисления в виде бинарного дерева и затем синтезируется дискретный аттрактор, фазовый портрет которого накрывает этот граф. Для решения поставленной задачи построим дискретный аттрактор с фазовым портретом в виде сильно ветвящегося дерева, в котором содержатся бинарные поддеревья вычисления всех возможных арифметических выражений, не превышающих определённый уровень сложности, ограниченный глубиной дерева вычисления. Работа аттрактора запускается загрузкой в вычислитель набора исходных операндов. Теговые коды исходных операндов позиционируют начальное состояние процесса на фазовом портрете. Дальнейшие события разворачиваются детерминировано и определяются конструкцией аттрактора и структурой фазового портрета. Правильно загруженный набор исходных операндов извлекает из фазового портрета своё бинарное поддерево. Следовательно, для программирования заданного вычисления необходимо отыскать, соответствующие ему листовые вершины и присвоить их коды исходным операндам в виде теговых сопровождений.

Для отыскания листовых вершин заданного вычисления необходимо наложить заданное бинарное дерево на общее сильно ветвящееся. Предполагается, что нумерация вершин предшественников увязана в таблицу кодирования арифметических операций. Размещение начинается с корневой вершины. Выбирается заключительная операция заданного вычисления и ставится маркер на вершину предшественницу корня, номер которой соответствует заключительной операции. Два операнда, участвующие в заключительной операции порождаются выполнением двух предшествующих арифметических операций, что обнаруживается при раскрытии скобок в направлении от главной заключительной операции. На следующем шаге необходимо поставить маркерные метки на двух вершинах, предшествующих отмаркированной на первом шаге. При этом следует отбирать вершины с номером, соответствующим кодам предшествующих арифметических операций. Если бы предшествующие операции всегда были разными, можно было бы ограничиться ветвлением общего дерева с кратностью равной четырём. Но в общем случае обе предшествующие операции могут быть одинаковыми. По этой причине в номерах предшествующих вершин каждая операция должна быть представлена дважды. Вот почему при четырёх операциях понадобилось дерево с кратностью ветвления равной восьми. Описанная процедура повторяется до исчерпания операций в исходной записи арифметического выражения. Последние маркерные метки отмечают листовые вершины бинарного дерева искомого вычислительного процесса. Результат программирования в данном случае это назначение теговых кодов исходным операндам. При загрузке в вычислитель исходные операнды запускают вычислительный процесс и извлекают требуемое бинарное поддерево путём прохождения своих маршрутов на фазовом портрете.

Разработанные ранее инструментальные средства дискретной динамики позволяют сконструировать компилятор, осуществляющий программирование процессов вычисления арифметических выражений в архитектуре самоопределяемых данных. Для этого есть инструменты формирования сильно ветвящихся деревьев, есть инструменты маскирования кодов для организации полной нумерации вершин предшественников, есть методы построения реверсивных аттракторов, обеспечивающих движение по фазовому портрету в прямом и обратном направлениях. Описанный компилятор можно сделать полностью автоматическим.

Поддержка полного сильно ветвящегося дерева необходима для работы компилятора, который должен содержать пути для вычисления всех возможных арифметических выражений. После выбора заданного выражения и завершения компиляции поддержка полных теговых кодов при исполнении процесса становится избыточной. Возможна оптимизация, которая означает сокращение разрядности тегов. Сокращение разрядности теговых кодов должно происходить при условии, что общая конструкция графа кодовых переходов не нарушается, выбранное бинарное поддерево сохраняется, а лишние ветви полного сильно ветвящегося дерева отсекаются. Такая задача может быть поставлена и есть предположения по её решению. Задача не имеет общего решения, это означает, что в каждом конкретном случае эффективность сокращения разрядности теговых сопровождений будет различной.

Приведем пример. Рассмотрим наложение функции на граф результата конкатенации трех функций побитового сдвига разрядности 4. Вышеописанным способом наложим на этот граф маску, предварительно поделив двоичное представление значений в его вершинах уже не на тройки, а на четверки. Составим таблицу соответствия кодов, не попавших под маску. Таким образом, применив эту таблицу к графу получим граф - фазовый портрет, где в вершинах уже стоят простейшие операции сложения, вычитания, умножения и деления. Теперь же построим граф нашей функции, где в листовых вершинах будут стоят операнды, а во всех остальных все те же простейшие операции. Целью задачи является поиск маршрута вычисления малого графа на большом, путем наложения одного на другой. Начиная с корневых вершин попарно сравним значения вершин в графах и подберем соответствующие по совпадению указанных в них операций . Результат наложения приведен на рис. 39. Отметим, что приведен не граф целиком, а лишь совпавший фрагмент. Проиллюстрировать наложение полностью не представляется возможным в силу большого размера графа.

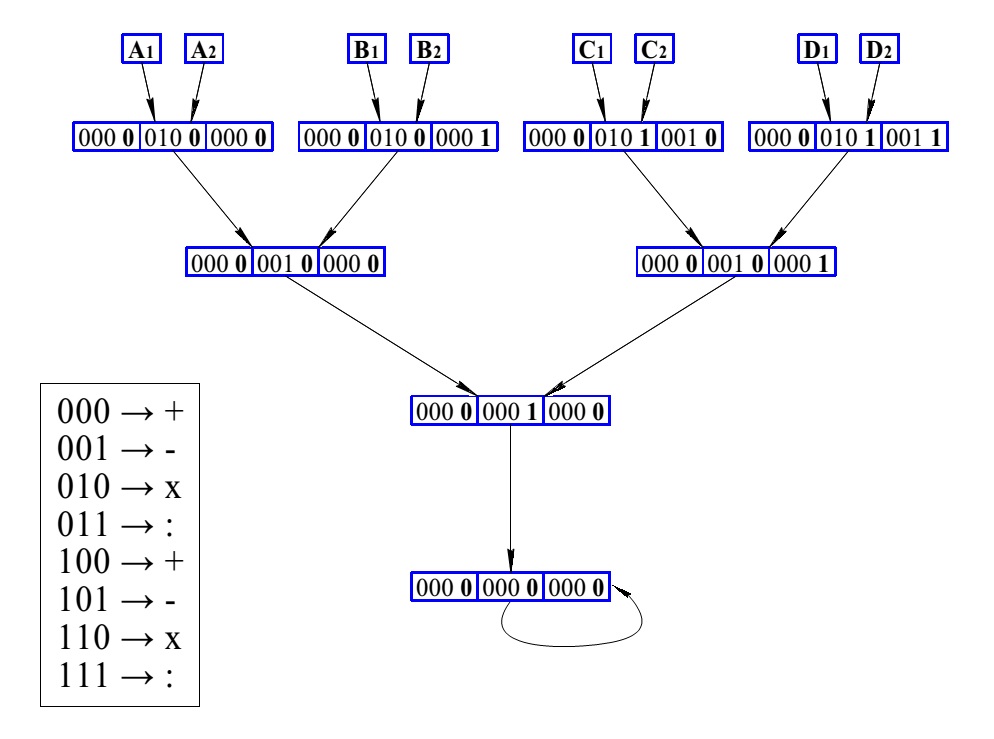
Рис. 39 Фрагмент наложения искомого графа на граф конкатенации.

ЗАКЛЮЧЕНИЕ

Оценка современного состояния технологии микроэлектронного производства позволяет сделать вывод о том, что в ближайшее десятилетие рост тактовой частоты прекратится и будет зафиксировано оптимальной значение 2.2 ГГц. При этом рост числа транзисторов продолжится и достигнет значений порядка десятка миллиардов на одном кристалле. Это означает, что закон Мура переформатируется в требование удвоения числа процессорных ядер с периодом 18 – 24 месяцев. Следовательно, основой роста производительности вычислительных средств в ближайшей перспективе становится освоение массового параллелизма. В работе показано, что рост производительности вычислительных средств в широком диапазоне значений параллелизма в общем случае не возможен. Обзор публикаций по опыту эксплуатации высокопараллельных систем показывает наличие эффекта быстрого насыщения роста производительности при значениях ускорения в 6-8 раз при 10-16 процессорных элементах для задач имеющих потенциал параллелизма в сотни и тысячи независимых событий. В работе были проанализированы и вскрыты причины подавления роста производительности, связанные с обменными операциями пересылки данных между параллельными ветвями процессов. Баланс временных затрат таков, что время счёта быстро падает и его вклад в общие затраты становится относительно ничтожным, но при этом агрессивно и устойчиво растут затраты на обмен данными. Сделан обзор современных и перспективных разработок по развитию обменной коммутационной среды. Показано, что ожидаемый рост производительности коммутационных сред не в состоянии переломить тенденции роста затрат на обслуживание параллелизма и способен только незначительно переместить точку насыщения роста производительности. Предпринят анализ эффективности организации вычислений в классической архитектуре, выведены экспертные оценки, показывающие, что КПД современного компьютера не превышает одного процента. Другими словами на одно полезное действие приходится не менее ста обеспечивающих затратных. Строить высокопараллельные системы при такой эффективности организации процессов бесперспективно, поскольку издержки растут кратно параллелизму, а быстро растущие специфические затраты на обслуживание параллелизма приводят опережающему росту суммарных издержек и делают массовый параллелизм бессмысленным. В работе проанализированы источники издержек и показано, что порождающей причиной являются фундаментальные принципы организации вычислений, основанные на идее централизованного управления разделении потоков команд и потоков данных. Данные хранятся в специальной среде хранения (памяти), а обрабатываются в среде обработки (процессорах). Для осуществления обработки необходимо осуществлять массовые пересылки данных из мест хранения к местам обработки и обратно. При массовом параллелизме эта проблема быстро обостряется и демонстрирует принципиальную несостоятельность архитектурной идеи. В качестве альтернативы предложена архитектура самоопределяемых данных, в которой реализован принцип слияния данных и командной информации в единый формат самоопределяемых операндов. Самоопределяемые операнды строятся аналогично пакетам в сетях пакетной коммутации и состоят из информационных полей, сопровождаемых набором командных полей, управляющих перемещением операндов, селекцией партнёров для обработки и выбором функций обработки. При этом реализуется принцип распределённого управления и устраняются паразитные пересылки – самоопределяемые данные обрабатываются там же где хранятся - в совмещённой функциональной среде. Таким образом создаётся перспектива эффективной реализации массового динамического параллелизма. При этом реализуется принцип распределённого управления, а это ставит проблему программирования самоопределяемых данных. Сделан выбор математического аппарата и излагаются основы дискретной динамики, Вводятся базовые понятия - дискретный аттрактор, фазовый портрет, реверсивный аттрактор и ряд других. Дискретная динамика описывает среду, в которой существуют, двигаются и обрабатываются самоопределяемые данные. В терминах дискретной динамики ставится и решается задача программирования самоопределяемых данных как задача синтеза фазовых портретов с заданной топологией. Описываются принципы построения компилятора, работа которого иллюстрируется на конкретном примере.

СПИСОК ЛИТЕРАТУРЫ

[1] Шайтан К.В., Антонов М.Ю., Шайтан А.К., Новоселецкий В.Н., Боздагонян М.Е., Касимова М.А. Метод молекулярной динамики в исследованиях свойств биологических объектов // Наноструктуры. Математическая физика и моделирование., 2012, 6 (1,2), 63-79.

[2] Блинов В.Н., Совенюк А.А. Программирование задач физики конденсированного состояния с использованием MPI // Наноструктуры. Математическая физика и моделирование., 2012, 7 (1), 5-107.

[3] Викул Е.А., Тужилин А.А. Геометрия аминокислот и полипептидов: случай рентгеноструктурного анализа // Наноструктуры. Математическая физика и моделирование., 2014, 11 (2), 5-29.

[4] Григоренко Б.Л., Князева М.А., Исаев Д.А., Новичкова А.В., Немухин А.В. Компьютерное моделирование химических реакций в сложных биологических системах // Наноструктуры. Математическая физика и моделирование., 2014, 10 (2), 95-107.

[5] Блинов В.Н. Дальнодействующие взаимодействия в компьютерном моделировании систем в конденсированном состоянии // Наноструктуры. Математическая физика и моделирование., 2014, 10 (1) 5-29.

[6] Ожигов Ю.И. Представление декогерентности при компьютерном моделировании квантовых состояний наносистем // Наноструктуры. Математическая физика и моделирование., 2013 8 (1) 47-65.

[7] Обзор продуктов семейства Tesla Kepler // NVIDIA.RU: NVIDIA Tesla GPU Accelerators, сайт производителя. URL:

http://www.nvidia.ru/content/tesla/pdf/NVIDIA-Tesla-Kepler-

[8] Черняк Л. Многоядерные процессоры и грядущая параллельная революция.// Открытые системы 2007 4 , 33-42.

[9] Воеводин В.В. Математические основы параллельных вычислений // ННГУ 2009 .583 стр.

[10] Sidlausakas D. Lecture on multicores // Danish National Research Foundation, Madalgo, 12.03.2013, p. 8. URL:

http://www.cs.au.dk/~gerth/ae13/slides/multicores.pdf

[11] Gene M. Amdahl. Validity of the single processor approach to achieving large scale computing capabilities // IBM Sunny vale, California. AFIPS spring joint computer conference. 1967. URL:

http://www-inst.eecs.berkeley.edu/~n252/paper/Amdahl.pdf

[12] Dennis J. B. First version of Data Flow procedure language // Lecture Notes in Computer Science 1974, 363 - 376.

[13] Городня Л.Г. Основы функционального программирования // М., 2004 280 с.

[14] Амамия М., Танака Ю. Архитектура ЭВМ и искусственный интеллект // Мир, Москва, 1993 397 с.

[15] Галушкин А.И., Точенов В.А. Транспьютерные системы – начало становления в России ЭВМ с массовым параллелизмом // Нейрокомпьютер, , 2005 3,   22-38.

[16] Backus J. Can Programming Be Liberated from von Neumann Style? A Functional Style and Its Algebra of programs // 1977 Turing Award Lecture, P. 63-130.

http://rkka21.ru/docs/turing-award/jb1977r.pdf

http://rkka21.ru/docs/turing-award/jb1977e.pdf

[17] Махиборода А.В. и другие, Система потоковой обработки информации с интерпретацией функциональных языков // Авторское свидетельство № 1697084 опубликовано 29. 06. 1989 г. Положительное решение 25.05 1990 г.

[18] Соколовский Ю.Л. Предпроектное исследование персональной ЭВМ редукционно-потокового типа средствами имитационного моделирования // Препринт 92-17, Институт кибернетики АН УССР, Киев 1992 30 стр.

[19] Cramer C. Board J. The Development and Integration of Distributer 3D FFT for a Cluster of Workstations // «4^th Annual Linux Showcase & Conference, Atlanta October 10-14 2000», Pp. 121–128 of the Proceeding.

[20] Морозов А.А., Тимофеев А.В. Эффективность параллельной реализации алгоритма Radix-4 быстрого преобразования Фурье // Наноструктуры. Математическая физика и моделирование., 2016 14 (1) 69-82.

[21] Duato J.,Yalamanchili S., Ni L. Interconnection Networks An Engineering Approach // MORGAN KAUFMANN PUBLISHERS, 2003.

[22] Borkar S., et al., iWarp: An integrated solution to high-speed parallel computing // Proceedings of Supercomputing'88, November 1988, 330-339.

[23] Kim J., Dally W.J., Scott S., Abts D. Technology-Driven, Highly-Scalable Dragonfly Topology // Northwestern University, Stanford University.

[24] Норман Г.Э., Орехов Н.Д., Писарев В.В., Смирнов Г.С., Стариков С.В., Стегайлов В.В., Янилкин А.В. Зачем и какие суперкомпьютеры экзафлопсного класса нужны в естественных науках // ПРОГРАММНЫЕ СИСТЕМЫ: ТЕОРИЯ И ПРИЛОЖЕНИЯ №4(27), 2015, 243–311.

[25] Yadav S., Mishra R., Gupta U. Performance Evaluation of Different Versions of 2D Torus Network // Computer Science and Engineering. 2015 International Conference on Advances in Computer Engineering and Applications.

[26] Dally W.J., Poulton J.W. Digital systems engineering // Cambridge University Press, New York, NY, 1998.

[27] Resources for Embedded and IoT Designers. URL: http://www.intel.com/design/network/products/optical/cables/index.htm

[28] Kim J., Dally W.J., Abts D. Flattened Butterfly : A Cost-Efficient Topology for High-Radix Networks // In Proc. of the International Symposium on Computer Architecture (ISCA), San Diego, CA, June 2007, 126–137.

[29] Leiserson C. Fat-trees: Universal networks for hardware efficient supercomputing // IEEE Transactions on Computer, C-34(10):892–901, October 1985.

[30] Дурнев В.Г., Стандрик В.Д.  // Основы построения систем передачи ЕАСС, Радиоисвязь 1985, 208 с.

[31] Мизин И.А., Богатырёв В.А., Кулешов А.П. Сети коммутации пакетов // Радио и связь. М. 1986 г 408 с.

[32] Мизин И.А., Махиборода А.В. Концепция самоопределяемых данных и архитектура распределённых систем // Информационные технологии и вычислительные системы, Москва, Наука, №1 , 1995 г., 21 - 31.

[33] Махиборода А.В. Проблемы создания вычислительных средств с непроцедурными внутренними языками // Управляющие системы и машины, №3 , 1993 г., 51 – 62.

[34] Арнольд В.И. Топология и статистика формул арифметики // Успехи математических наук 2003 г. том 58, вып. 4 (352), 3- 28.

[35] Арнольд В.И. Топология алгебры: комбинаторика операции возведения в квадрат // Функциональный анализ и его приложения 2003. т 37, вып 3, 20-35.

[36] Арнольд В.И. Сложность конечных последовательностей нулей и единиц и геометрия конечных функциональных пространств // Математический институт им. В. А. Стеклова, Москва, 13.05.2006.