
Урна содержит 10 занумерованных шаров с номерами от 1 до 10. Шары извлекаются по одному без возвращения
 |
 |
Математика |
 |
 |
Решение задачи |
 |
 |
|
 |
 |
Выполнен, номер заказа №16082 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
|
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл! |
|
Закажите у меня новую работу, просто написав мне в чат! |
Урна содержит 10 занумерованных шаров с номерами от 1 до 10. Шары извлекаются по одному без возвращения. Рассматриваются следующие события: 𝐴 – номера шаров в порядке поступления образуют последовательность 1, 2, …, 10; 𝐵 – хотя бы один раз совпадает номер шара и порядковый номер извлечения; 𝐶 – нет ни одного совпадения номера шара и порядкового номера извлечения. Определить вероятности событии 𝐴, 𝐵, 𝐶. Найти предельные значения вероятностей при бесконечном увеличении числа шаров.
Решение
По классическому определению вероятности, вероятность события 𝐴 равна где 𝑚 – число благоприятных исходов, 𝑛 – общее число исходов. а) Основное событие 𝐴 – номера шаров в порядке поступления образуют последовательность 1, 2, …, 10. Первым должен быть извлечен шар номер 1 (такой шар 1 из 10): Вторым должен быть извлечен шар номер 2 (такой шар 1 из 9 оставшихся): Аналогично Вероятность события 𝐴 по формуле произведения вероятностей равна: б) Основное событие 𝐵 – хотя бы один раз совпадает номер шара и порядковый номер извлечения. Определим вероятность противоположного события 𝐵̅ – нет ни одного совпадения номера шара и порядкового номера извлечения. Первым должен быть извлечен шар не с номером 1 (таких шаров 9 из 10): Вычислим вероятность того, что вторым извлекут шар с номером 2. Его не должны извлечь первым и извлечь на втором. Тогда вероятность того, что вторым извлечется не шар №2: Найдем вероятность того, что третьим шаром извлечется шар с №3 (т.е. его не должны извлечь при первом и втором извлечении и извлечь на третьем): И вероятность того, что не извлекут на третьем шар с №3: Аналогично и с другими шарами. Получим, что вероятность того, что отдельный шар будет извлечен в порядке, не соответствующим его номеру: . Тогда в) Основное событие 𝐶 – нет ни одного совпадения номера шара и порядкового номера извлечения. Это событие противоположно событию 𝐵, значит: Найдем предельные значения вероятностей при бесконечном увеличении числа шаров Ответ: 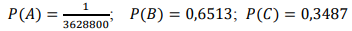

Похожие готовые решения по математике:
- Из 25 студентов 10 занимаются научной работой на кафедре СМ-4; 8 – на кафедре СМ-5; остальные
- Из колоды в 36 карт вынимают без возвращения 6 карт. Найти вероятность того, что ровно две карты тузы
- В урне 3 белых, 7 черных и 4 синих шара. Из нее вынимают наудачу 3 шара. Найти вероятность того
- Среди 10 команд, участвующих в КВН, 3 команды из Петербурга и 3 – из Москвы. Для участия в конкурсе
- В группе 21 человек. Какова вероятность того, что у них разные дни рождения
- Среди 6 приборов имеется два неисправных. Приборы проверяются по очереди до выявления обоих неисправных
- В урне 5 белых и 5 черных шаров. Из этой урны последовательно извлечены все шары по одному и разложены в ряд
- Урна содержит 7 занумерованных шаров с номерами от 1 до 7. Шары извлекаются по одному без возвращения. Рассматриваются
- Все избиратели разбиты на три возрастных группы: младшая, средняя и старшая. При этом объем младшей группы составляет 20%, а средней
- Из 20 пар обуви 2 пары – белого цвета, 8 – черного, а остальные – цветные. Одна пара белой, 4 пары черной и 2 пары цветной – 36 размера
- В магазин привезли телевизоры двух фирм. Известно, что количество телевизоров, изготовленных первой фирмой
- Покупатель приобретает хлеб в одном из трех магазинов. Свежий хлеб бывает в первом магазине с вероятностью 0,6; во втором

